RESEARCH ARTICLE

 

DFT+U Study of the Electronic, Magnetic and Mechanical Properties of Co, CoO, and Co₃O₄

 

 

Abdelaziz Cadi-Essadek^I; Alberto Roldan^I; David Santos-Carballal^{I, II, ≠}; Phuti E. Ngoepe^II; Michael Claeys^III; Nora H. de Leeuw^I,^≠,^*

^ISchool of Chemistry, Main Building, Cardiff University, Park Place, CF10 3AT, Cardiff, United Kingdom
^IIMaterials Modelling Centre, University of Limpopo, Private Bag X1106, Sovenga, 0727, South Africa
^IIIDepartment of Chemical Engineering, Catalysis Institute and c*change (DST-NRF Centre of Excellence in Catalysis), University of Cape Town, Private Bag X3, Rondebosch, 7701, South Africa

 

 

---

ABSTRACT

Cobalt nanoparticles play an important role as a catalyst in the Fischer-Tropsch synthesis. During the reaction process, cobalt nanoparticles can become oxidized leading to the formation of two phases: CoO rock-salt and Co₃O₄ cubic spinel. Experimentally, it is possible to evaluate the phase change and follow the catalyst degradation by measuring the magnetic moment, as each material presents a different magnetic structure. It is therefore important to develop a fundamental description, at the atomic scale, of cobalt and its oxide phases which we have done here using density functional theory with the Dudarev approach to account for the on-site Coulomb interactions (DFT+U). We have explored different U_eff values, ranging from 0 to 5 eV, and found that U_eff = 3.0 eV describes most appropriately the mechanical properties, as well as the electronic and magnetic structures of Co, CoO and Co₃O₄. We have considered a ferromagnetic ordering for the metallic phase and the antiferromagnetic structure for the oxide phases. Our results support the interpretation of the catalytic performance of metallic cobalt as it transforms into its oxidized phases under experimental conditions.

Keywords: Materials chemistry, cobalt oxides, cobalt metal, spinel, density functional theory, on-site Coulomb correction.

---

 

 

1. Introduction

Supported cobalt nanoparticles play an important role as catalysts in the Fischer-Tropsch synthesis (FTS),^1,2 which is a surface polymerization reaction producing hydrocarbon chains from syngas (mixture of H₂ and CO). Recent investigations have concentrated their efforts on the link between the optimum performance of the nanoparticles and their structure.^3-5 Other investigations have focused on the deactivation of the cobalt nanoparticles by oxidation from water and related this process to the size of the nanoparticles.^6-8 Indeed, H₂O, a by-product of FTS, has an important effect on the deactivation of cobalt-based FT catalysts. Claeys and co-workers^9,10 showed a correlation between the cobalt nanoparticle's size and its deactivation, which is a consequence of complex re-oxidation mechanisms leading to the formation of the inactive cobalt oxide phase (CoO). To track the deactivation process and the phase change, Claeys and collaborators⁹ used a magnetometer and reduced tricobalt tetroxide (Co₃O₄) to metallic cobalt. The phase change modifies the magnetization, thereby generating a signal in the magnetometer. The initial Co₃O₄, which also has potential applications in several fields of catalysis,^1,2,11-16 was reduced stepwise to CoO and then to metallic Co.⁹ This process led to a change from an antiferromagnetic to a ferromagnetic structure. The opposite process, i.e. Co oxidation, would lead to CoO before forming Co₃O₄. Therefore, a description of the Co oxidation to CoO and then Co₃O₄ is crucial for understanding and designing the properties of the catalyst nanoparticles.¹⁷

A key to controlling the FTS process on Co-based catalysts is to understand the catalyst and active species, where computational modelling can help to explain any structure-activity relationships. Previous theoretical studies have investigated independently the metallic cobalt and oxide phases, but a common protocol to describe accurately all three materials is required, i.e. a common computational setup for representing the electronic and mechanical properties. Thus, the goal of this investigation is to determine a common computational methodology, based on the Density Functional Theory (DFT) to describe accurately the electronic and geometric structures of Co, CoO, and Co₃O₄.

DFT commonly underestimates the band gap and magnetic moment of materials where the valence electrons are highly localized,¹⁸ such as Co metal and Co oxides. Here, we therefore adopt the DFT+U^19-22 method to describe correctly the electronic and geometric properties of Co, CoO and Co₃O₄. DFT+U is a correction of the pure DFT method, where the U parameter is a Hubbard-like potential added to the Kohn-Sham DFT Hamiltonian. DFT+U usually provides accurate results for 3d transition metal oxides, hence the use of this method in our investigation. We have considered several U parameters, ranging from 0 to 5 eV in order to calculate the lattice parameters, the band gaps, the total magnetic moments, and the bulk moduli of the materials, following the procedure used in previous works.^23-25

 

2. Computational Methods

We have carried out the calculations using the Vienna Ab-initio Simulation Package (VASP),^26-29 which solves the Kohn-Sham equations in a periodic framework.³⁰ All calculations were spin polarized and we have employed the generalized gradient approximation (GGA) with the Perdew-Burke-Ernzerhof (PBE)³¹ as the density functional. The long-range dispersion interactions were described by the semi empirical method of Grimme (DFT-D3).³² We have considered the dispersion effects for modelling these metallic and ionic bulk phases here, as we expect in future work to study the catalytic properties of the surfaces of these materials, where this correction plays a major role.^33-44 We have used the Dudarev approach²² to describe the d electrons of the metal atoms, in the DFT+U⁴⁵ scheme, as implemented in the VASP software. Note that the U used in this investigation is the effective Hubbard U_eff = U-J where J is considered equal to zero. The core electrons up to and including the 3p levels of Co and the 1s of O were considered as frozen states and the projected augmented wave method (PAW)⁴⁶ was used to evaluate the interaction between the core and the valence electrons. To determine the number of plane-waves required, we have run energy convergence tests and found that 500 eV is sufficient to properly describe the three materials, i.e. Co, CoO, and Co₃O₄. The geometry optimizations were performed using the conjugate gradient technique with an ionic convergence criterion of 0.01 eV/A. Both the shape and the volume of the cell were allowed to change to obtain the ground state lattice. The reciprocal space was sampled by a 21 x 21 x 21 mesh of k-points for both Co and CoO bulks, while for Co₃O₄an 8 x 8 x 8 mesh of k-points was used.

Cobalt. Metallic cobalt (Co) has three crystal structures: hexagonal close-packed (hcp) (a-phase), face centred cubic (fcc) (ß-phase) and primitive cubic phase (e-phase). Under room conditions, the hcp cobalt is more stable than the fcc phase, while above 450 °C the ß-phase becomes the most stable structure.⁴⁷ Additionally, it has been observed that the FTS is facilitated by an hcp Co catalyst.^48-50 Thus, we discuss only the catalytically important cobalt hcp phase, whose primitive unit cell is shown in Fig. 1a.

 

 

Cobalt oxide. Metal monoxides such as CoO have a rock-salt NaCl crystal structure (R3m) and the most stable magnetic ordering below its Néel temperature is the antiferromagnetic type II (AF-II). In the AF-II ordering, the metal atoms located on the (111) plane present a ferromagnetic ordering, while the metal atoms on two adjacent planes have an antiferromagnetic arrangement.^51,52 In the solid state calculations, this magnetic ordering cannot be represented as there is a geometrical frustration in the CoO crystal structure. Thus, to investigate the AF-II structure, we have considered a rhombohedral four-atom unit cell (R3m space group) (Fig. 1b), which is equivalent to the geometry used in previous theoretical studies where the authors investigated the electronic and magnetic structures of CoO.^53,54

Tricobalt tetroxide Co₃O₄. The mixed oxidation state cobalt oxide has a normal spinel structure with a formula unit represented as (A)[B]₂O₄, where A and B represent Co²+ and Co³+, respectively. The magnetically active Co²⁺ are located in the tetrahedral site. Co³+ are located in the octahedral site, leadingto a complete occupation of the low energy t_2g orbitals and therefore those atoms do not have a permanent magnetic moment.⁵⁵ Below the Néel temperature (~40 K), the stable magnetic structure is the collinear antiferromagnetic ordering of the spins within the tetrahedral sites.^55-57 Figure 1c shows the crystal structure of Co₃O₄ and its magnetic ordering where neighbouring Co²⁺ have opposite orientated high-spin states (S = 3/2).

 

3. Results

3.1. U Parameters Fitting

3.1.1. Cell Parameter

The calculated values of the lattice parameter for Co, CoO, and Co₃O₄, as a function of U values, are shown and compared with previous experimental studies in Table 1. The c/a ratio for Co, which is defined as the ratio of the lattice parameters c and a, increases from 1.616 to 1.801 for a range of U values between 0.0 and 4.0 eV, then it falls to an average of 1.587 at U = 4.5 and 5.0 eV The calculated values are close to the experimental one obtained from the X-ray bond's method, c/a = 1.623,⁵⁸ with the highest percentage error of 12 % (Fig. 2).

 

 

The cell lattice of the CoO cubic cell ranges from 4.259 to 4.349 A as a function of U (Table 1), which is in good agreement with the experimental value (4.26 A).^59,60 Indeed, we have a maximum percentage error of only 2.1 % for U = 1.5 eV (Fig. 2). The cell shape was freely relaxed during the geometry optimization, which led to a monoclinic distortion, Aß = ß -125.264 °, ranging from -1.42 ° for U = 2.5 eV to 0.32 ° for U = 4.0 eV. The best agreement with experimental findings (∆ß = 0.30 °)⁶⁰ was found for U = 3.0 eV (∆ß = 0.19 °), whereas Schrön et al.⁶²used DFT+U to calculate a monoclinic distortion of 0.80 °.

The Co₃O₄ cubic lattice parameter also increases with the U value from 8.053 to 8.099 A (Table 1). Comparing to the experimental value (a = 8.086 A)⁶¹, the minimum percentage error (0.01 %) corresponds to U = 3.0 eV (Fig. 2). Contrary to CoO, the unit cell does not suffer any distortion if the cell shape is allowed to relax freely, which is expected for spinels containing only one type of cation.⁶³ Concerning the bond angle analysis, similarly to Selcuk et al.,⁶⁴ we only find a distortion for the O-Co³+-O angles, while the O-Co²⁺-O angles keep the same value upon bulk optimization.

3.1.2. Mechanical Properties

We have calculated the bulk modulus for each of the three materials as a function of the U value (Table 2). The calculated bulk moduli for pure Co are all in the same order as the experimental values and the bulk modulus derived using U = 2.5 eV is within the range of experimental values (191⁶⁵-199.6⁶⁶) (Fig. 2).

 

 

The bulk modulus of CoO was reported experimentally to be 181 GPa⁶⁸ and subsequently confirmed by shock and static experiments to be 179 GPa.⁶⁷ Our best agreement with the experimental results was again found for U =2.5 eV where we calculated a value of 182 GPa (Fig. 2). Our result using DFT-D3 + U is close to the one obtained using hybrid functionals (214.92 GPa).⁷⁰

The bulk modulus of the Co₃O₄ material was evaluated experimentally to be 189 GPa,⁶⁹ which is similar to the PBE+U value (192 GPa) calculated by Chen et al.⁷¹However, our derived values using DFT+U range from 232 to 249 GPa and therefore overestimate the Co₃O₄ compressibility as the bulk modulus represents the resistance to fracture of a materials. The smallest percentage error was found for U = 5.0 eV (22.75 %) (Fig. 2).

From our calculations (Table 2 and Fig. 2) we note that the value of U = 2.5 eV gives the best agreement with the experimental results for both Co and CoO materials. Concerning Co₃O₄, our calculated values are generally overestimating the bulk modulus compared to the experimental result (189 GPa⁶⁹). However, our calculations are based on a perfect and pure single crystal, whereas the presence of impurities and defects, which are difficult to control in experimental samples, may play a key role in influencing the bulk modulus. Thus, if our calculations of the bulk modulus for Co₃O₄ are correct, as suggested by the excellent agreement with experiment for Co and CoO, then the non-perfect nature of the experimental Co₃O₄ material makes it less resistant to fracture, compared to the perfect material considered in our calculations.

3.1.3. Electronic Structure

We show in Table 3 the magnetic moment per Co atom and the band gap as a function of the U value for Co, CoO and Co₃O₄ bulks.

 

 

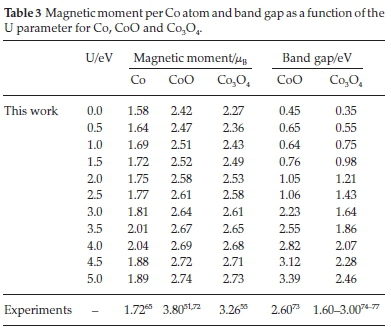
We note an increase of the magnetic moment in line with the d-correlation for metallic Co, from 1.58 to 2.04 ,u_B. The best agreement with the experimental value (1.72 ,u_B⁶⁵) is found for U = 1.5 eV. However, for the range of U = [0.5-3] eV, the percentage error is relatively small, at less than 5.5 % (Fig. 2), in good agreement with previous GGA+U reports.⁴⁷

The calculated magnetic moment per Co atom in the oxides also increases with the U parameter. In the case of CoO, it is underestimated by ~1 ,u_B compared to the experimental values.^51,60,72 The disparity with experiment is attributed to the inaccurate description of the angular momentum of Co²+, which is not totally quenched by the crystal field.⁵² We could have increased the U parameter to agree better with the experimental magnetization value, but that would have compromised the accuracy of the lattice parameters and the band gap. However, our calculated magnetic moments fall in the range of previous theoretical studies (2.63-2.74 ,μ_B).^19,52,78,79

The poor treatment of the Co²⁺ angular momentum is also reflected in Co₃O₄. The values in Table 3 are equivalent for all the Co²⁺ and we should bear in mind that the magnetic moment indicates the absolute value and may be negative or positive depending on the spin orientation. Experimental magnetic moment measurements of the Co²⁺ atom have indicated a value of 3.26 μ_Bin Co₃O₄⁵⁵, which is ~0.5 ,μ_B larger than our calculation using U = 5.0 eV. Singh et al.⁸⁰used DFT+U (U = 4.4 eV for the Co²⁺ ions and 6.4 eV for the Co³⁺ ions) to derive a magnetic moment of Co²+ of 2.71 ,μ_B. They have also employed hybrid functional calculations, which calculated a value of 2.66 ,μ_B. Walsh et al.⁸¹also used DFT+U (U = 2.0 eV) and reported a similar value for the Co²+ magnetic moments, i.e. 2.52 ,μ_B.

We therefore consider that any U parameter bigger than 3 eV describes as accurately as is possible the magnetic moment of CoO and Co₃O₄.

Similarly to the magnetization, the band gap (Table 3) increases with the U parameter. In the case of CoO, Kurmaev et al.⁷³found a value of 2.60 eV using synchrotron-excited oxygen X-ray K-emission spectroscopy. Forti et al.⁵⁴used DFT+U (U = 4.0 eV), including spin orbit coupling (SOC), to calculate a band gap of 2.81 eV, which is very close to our calculated value (2.82 eV), indicating the negligible effect of SOC in this material.

The accepted experimental band gap values found in the literature for Co₃O₄ ranges from 1.6 to 3.0 eV.^74-77 However, infrared optical spectroscopy has found a band gap of 0.76 eV,⁸² whereas the use of long-lived photoexcited carrier dynamics of d-d excitation⁸³ measured an optical band gap of 0.82 eV There are also discrepancies in previous theoretical band gap calculations of Co₃O₄. Lima⁸⁴ used hybrid calculations, which led to a band gap of 0.72 eV in agreement with the experimental study made by Qiao et al. (0.76 eV)⁸² and with our result (for U = 1.0 eV). They found that SOC was not essential for the description of Co₃O₄. However, another study made by Walsh et al.⁸¹using DFT+U (U = 2.0 eV) determined a band gap of 1.23 eV The discrepancies between the different studies concerning the Co₃O₄ band gap shows that the description of this property is still under debate.

To determine the U value that describes correctly the geometry of the three materials, we have considered a percentage error cut off of 2.5 % as a good estimation of the cell lattice. We note from Fig. 2 that for Co, CoO and Co₃O₄, the percentage error to describe the bulk geometry is smaller than 2.5 % for the range of U values [0, 3] eV and U = [4.5, 5] eV. The accuracy of the bulk modulus is compromised for Co₃O₄, but U ~3.0 eV provides a suitable description for the rest of the materials.

A U value of ~3.0 eV also describes adequately the magnetic moment of the three materials and the band gap of both CoO and Co₃O₄. As we will consider a system containing pure Co and its oxides in future investigations, we need to determine one U value that describes, with an acceptably small percentage error, the properties of the three materials at the same time. We will therefore ensure that the formation energies of the cobalt oxide phases are in good agreement with experiment results.⁸⁵ Thus, an effective increment of the on-site Coulomb repulsion in the Co d electrons by 3 eV is a fair compromise to investigate the physical and chemical properties of Co, and its oxides, although a single U value cannot describe accurately all the properties of the three solids.^64,86-89

3.2. Electronic and Mechanical Properties for U = 3 eV

We have adoptedU=3eVtodescribe and discuss in more detail the electronic structure, elastic constants, and mechanical properties of Co, CoO and Co₃O₄.

We have determined the interatomic distances for the three materials and found the Co-Co distance in metallic Co to equal 2.427 A, which is comparable to previous experimental findings (2.497 A).⁴⁷ In the CoO bulk, we have determined a Co-O distance of 2.142 A, which is in agreement with previous reports (2.13 Ã).⁵⁹ In Co₃O₄, the Co³+-O and Co²+-O distances are 1.920 and 1.937 A, respectively, which is comparable to a previous theoretical investigation⁶⁴ (Co³+-O = 1.926 A and Co²+-O = 1.929 A), whereas another theoretical study determined the followingdistances: Co³+-O = 1.93A and Co²+-O = 1.94A.⁸¹ Our calculated Co³⁺-O and Co²⁺-O distances are also in good agreement with the experimental result (Co³⁺-O = 1.923 A and Co²+-O = 1.928 A) reported by Liu et al.⁹⁰

In Fig. 3, we show the total and projected density of states (DOS) of Co, CoO and Co₃O₄ materials. The asymmetric up and down spin channels show the ferromagnetic characteristic of metallic cobalt, where the shift of the band centre in the minority spin towards higher energies has also been observed in previous theoretical studies.^47,91

The total magnetization of CoO is zero as the DOS of the up and down spin channels are symmetric (Fig. 3). Indeed, the three unpaired electrons of each cobalt atom in the four-atom unit cell present an antiferromagnetic ordering as shown in (Fig. 1b). We note that the valence band is composed by the Co 3d orbitals and O 2p orbitals, while the contribution of anion orbitals to the conduction band is negligible. Similar results were shown by Archer et al.⁹²and Wdowick et al.⁵²who used DFT+U methodology to show the hybridization of the Co 3d orbitals with the O 2p orbitals in the valence band, while the conduction band is composed only by Co 3d. More precisely, the valence band maximum is mainly composed by the O 2p orbitals and the Co t_2g orbitals, while the conduction band minimum is dominated by the Co 3d orbitals.

We have also computed the J₁ couplingbetween the nearest Co neighbours (Equation 1), where S = 3/2 and E_AFM and E_FM are the total energies of the antiferromagnetic and ferromagnetic structures, respectively. Our J value (15.69 meV) is double the one determined by Deng et al.⁹³(8.00 meV), who used U = 5.1 eV and J = 1.0 eV to describe the rocksalt CoO bulk.

In the case of Co₃O₄, we note from Fig. 3 that the DOS is mainly constituted of the Co³+ d orbitals, for the band energies between -1.5 and -0.5 eV Moreover, it is equally formed by the d-Co³+, d-Co²+ and 2p O orbitals between -0.5 eV and the Fermi energy. In the conduction band, the Co³⁺ d-orbitals are less dominant and the contribution of O p orbitals and Co²⁺ d-orbitals is non-negligible, in good agreement with previous experimental and theoretical investigations, which have also demonstrated that the Co³+ d-orbitals prevail in the valence band.^64,71,94 Additionally, from the projection of the Co³⁺ orbitals, we noted that the valence band is composed of t_2g orbitals and the conduction band is composed of e_g orbitals. The symmetrical plot of the Co³+ DOS confirms that all the t_2g orbitals are filled with six electrons, while the e_g oribitals are empty. Thus, our computational results validate the magnetic structure: S=0(t_2g⁶ e_g⁰), showing that the Co³+ atom in spinels has the same behaviour regardless whether it occupies the tetrahedral or octahedral position.⁹⁵

In Co²+, the down spin states of the t₂ orbitals are located in the valence band, while the spin-up states are located in the conduction band (Fig. 3). We observe that most of the e orbitals are located at a higher energy than the t₂ orbitals and both alpha and beta states are located in the valence band, but at different energies (non-symmetric plot). These show the magnetic configuration of Co²⁺ to be S = 3/2 (e_g⁴ t_2g³), which confirms that the magnetization in the Co₃O₄ bulk comes from the Co²⁺ atoms with their unpaired electrons, which is in good agreement with the study made by Chen et al.⁷¹It also suggests that the magnetic properties of this atom in a spinel do not depend on the cation filling the octahedral holes.⁹⁵

We have next computed the J₁ exchange coupling between the nearest Co²⁺ neighbours (Equation 2):

where S = 3/2 and E_AFM and E_FM are the total energies of the antiferromagnetic and ferromagnetic structures, respectively. In this work, we determined a value of J₁ = -4.28 meV, which is close to the value reported in a previous experimental investiga-tion.⁵⁶ Another theoretical investigation made by Chen et al.⁷¹ reported a value of-5.0 meV using hybrid functionals. However, the same authors determined a value of 0.1 meV using DFT+U as their U_eff parameter is larger than ours: they chose U_eff = 4.4 and 6.7 eV for Co²⁺ and Co³⁺, respectively.

In Table 4, we summarize the calculated independent elastic constants for the hcp crystal symmetry of Co (C₁₁,C₁₂,C₁₃,C₃₃, C₄₄, and C₆₆). We note that C₁₂ and C₁₃ are in good agreement with previous theoretical and experimental investigations,^96,97 but for the other elastic constants, we found a discrepancy of more than 25 %. This discrepancy may arise from the choice of the U parameter: here we consider U = 3.0 eV while Kuang et al.⁹⁶chose an on-site Coulomb interaction U = 2.8 eV and on-site exchange interaction J = 1.0 eV. Guo et al.⁹⁸have also used DFT (GGA) to evaluate the elastic constants and their results are in the same range as ours.

 

 

The elastic constants of CoO compare well with previous theo-retical⁵² and experimental investigations⁹⁹, showing a percentage error of less than 12 % compared with the experimental findings for the three independent elastic constants, i.e. C₁₁,C₁₂, and C₄₄^.

The calculated values of the independent elastic constants of Co₃O₄ (C₁₁ = 307.80, C₁₂ = 145.80, and C₄₄ = 104.43) are in the same range as the ones found for CoO. We compare our calculated elastic constants for Co₃O₄ with those simulated for the very-well characterized magnetite Fe₃O₄⁶³ as, to the best of our knowledge, there is no information on the experimental elastic constants for Co₃O₄ in the literature. The normal and shear strains, which are perpendicular and parallel distortions to the cell faces, lead to the elastic constants C₁₁ and C₄₄, respectively, which have higher values for Co₃O₄, suggesting that this spinel oxide is harder and more difficult to compress than its iron counterpart. However, the elastic constant C₁₂, which measures the distortion along two different axes is 14.1 GPa larger for magnetite, indicating that the cobalt spinel is slightly easier to deform in this direction compared to Fe₃O₄.

 

4. Conclusion

We have studied the mechanical and electronic properties of Co, CoO and Co₃O₄, considering U values ranging from 0 to 5 eV The calculated bulk properties, i.e. cell parameter, bulk modulus, magnetic moment, and band gap for all the materials, were in fair agreement with previous theoretical and experimental studies for U = 3.0 eV. We have therefore chosen this latter value to describe the electronic and magnetic structures, and the elastic constants of the three materials. We have shown, from the DOS plots that metallic cobalt is ferromagnetic, while both cobalt oxides, CoO and Co₃O₄, present an antiferromagnetic structure. In CoO, the metal atoms belonging to the same (111) plane have a ferromagnetic ordering, while the metal atoms on two adjacent (111) planes present an antiferromagnetic ordering. In Co₃O₄, the magnetization comes from the Co²⁺ atoms as they have unpaired electrons and the neighbouring Co²⁺ have opposite high-spin state (S = 3/2). U = 3.0 eV also describes correctly the band gaps of both CoO and Co₃O₄ materials. Finally, the calculated elastic constants are in fair agreement with previous theoretical and experimental studies, except for the C₃₃ and C₆₆ of metallic Co.

 

Acknowledgements

We acknowledge the Engineering & Physical Sciences Research Council (EPSRC grant no. EP/K016288/1) for funding and the Economic and Social Research Council for funding of a Newton UK-South Africa International PhD Partnering programme (grant no. ES/N013867/1). We acknowledge the use of the Centre for High Performance Computing (CHPC) facility of South Africa in the completion of this work. Via our membership of the UK's HEC Materials Chemistry Consortium, which is funded by EPSRC (EP/L000202/1 and EP/R029431/1), this work used ARCHER, the UK National Supercomputing Service (http://www.archer.ac.uk). This work was performed using the computational facilities of the Advanced Research Computing @ Cardiff (ARCCA) Division, Cardiff University. The authors also acknowledge the use of HPC Wales, and associated support services, in the completion of this work. All data created during this research are openly available from the Cardiff University's Research Portal at http://doi.org/10.17035M.2018.0061874165

 

ORCID iDs

A. Roldan: orcid.org/0000-0003-0353-9004

D. Santos-Carballal: orcid.org/0000-0002-3199-9588

N.H. de Leeuw: orcid.org/0000-0002-8271-0545

 

References

1 Schulz, H., Short history and present trends of Fischer-Tropsch synthesis, Appl. Catal. A Gen., 1999,186, 3-12.         [ Links ]

2 M.E. Dry, Fischer-Tropsch synthesis over iron catalysts, Catal. Letters, 1990, 7, 241-251.         [ Links ]

3 A . Tuxen, et al., Size-dependent dissociation of carbon monoxide on cobalt nanoparticles, J. Am. Chem. Soc., 2013,135, 2273-2278.         [ Links ]

4 G. Prieto, A. Martínez, P. Concepción and R. Moreno-Tost, Cobalt particle size effects in Fischer-Tropsch synthesis: structural andin situ spectroscopic characterisation on reverse micelle-synthesised Co/ITQ-2 model catalysts, J. Catal., 2009, 266, 129-144.         [ Links ]

5 G.L Bezemer, et al., Cobalt particle size effects in the Fischer-Tropsch reaction studied with carbon nanofiber supported catalysts, J. Am. Chem. Soc., 2006, 128, 3956-3964.         [ Links ]

6 A. Tavasoli, A. Nakhaeipour and K. Sadaghiani, Raising Co/Al₂O₃ catalyst lifetime in Fischer-Tropsch synthesis by using a novel dual-bed reactor, Fuel Process Technol., 2007, 88, 461-469.         [ Links ]

7 M. Claeys, et al., Impact of process conditions on the sintering behavior of an alumina-supported cobalt Fischer-Tropsch catalyst studied with an in situ magnetometer, ACS Catal., 2015, 5, 841-852.         [ Links ]

8 J. van de Loosdrecht, et al., Cobalt Fischer-Tropsch synthesis: deactivation by oxidation?, Catal. Today, 2007,123, 293-302.         [ Links ]

9 N. Fischer, B. Clapham, T. Feltes, E. van Steen and M. Claeys, Size-dependent phase transformation of catalytically active nanoparticles captured in situ, Angew Chem. Int. Edn., 2014, 53, 1342-1345.         [ Links ]

10 M. Wolf, H. Kotzé, N. Fischer and M. Claeys, Size dependent stability of cobalt nanoparticles on silica under high conversion Fischer-Tropsch environment, Faraday Discuss., 2017,197, 243-268.         [ Links ]

11 F. Jiao and H. Frei, Nanostructured cobalt oxide clusters in meso-porous silica as efficient oxygen-evolving catalysts, Angew Chem. Int. Edn., 48, 2009, 1841-1844.         [ Links ]

12 L. Hu, Q. Peng and Y. Li, Selective synthesis of Co₃O₄ nanocrystal with different shape and crystal plane effect on catalytic property for methane combustion, J. Am. Chem. Soc., 2008,130, 16136-16137.         [ Links ]

13 X. Xie, Y. Li, Z.-Q. Liu, M. Haruta and W. Shen, Low-temperature oxidation of CO catalysed by Co₃O₄ nanorods, Nature, 2009, 458, 746-749.         [ Links ]

14 Y. Liang, et al., Co₃O₄ Nanocrystals on graphene as a synergistic catalyst for oxygen reduction reaction, Nat. Mater., 2011,10, 780-786.         [ Links ]

15 J. Xu, P. Gao and T.S. Zhao, Non-precious Co₃O₄ nano-rod electro-catalyst for oxygenreduction reaction in anion-exchange membrane fuel cells, Energy Environ. Sci., 2012, 5, 5333-5339.         [ Links ]

16 A.J. Esswein, M.J. McMurdo, P.N. Ross, A.T. Bell and T.D. Tilley, Size-dependent activity of Co₃O₄ nanoparticle anodes for alkaline water electrolysis, J. Phys. Chem. C, 2009, 113, 15068-15072.         [ Links ]

17 D.H. Ha, L.M. Moreau, S. Honrao, R.G. Hennig and R.D. Robinson, The oxidation of cobalt nanoparticles into Kirkendall-Hollowed CoO and Co₃O₄: the diffusion mechanisms and atomic structural transformations, J. Phys. Chem C., 2013,117, 14303-14312.         [ Links ]

18 P. Khatri and M.N. Huda, Application of attractive potential by DFT+Utopredict the electronic properties of materials without highly localized bands, Comput. Mater. Sci., 2014, 81, 290-295.         [ Links ]

19 V.I. Anisimov, J. Zaanen and O.K. Andersen, Band theory and Mott insulators: Hubbard U instead of Stoner I, Phys. Rev B, 1991, 44, 943-954.         [ Links ]

20 A.I. Liechtenstein, V.I. Anisimov and J. Zaanen, Density-functional theory and strong interactions: orbital ordering in Mott-Hubbard insulators, Phys. Rev. B, 1995, 52, 5467-5471.         [ Links ]

21 V.I. Anisimov, I.V. Solovyev, M.A. Korotin, M.T. Czyyk and G.A. Sawatzky, Density-functional theory and NiO photoemission spectra, Phys. Rev. B, 1993, 48, 16929-16934.         [ Links ]

22 S.L. Dudarev, G.A. Botton, S.Y. Savrasov, C.J. Humphreys and A.P. Sutton, Electron-energy-loss spectra and the structural stability of nickel oxide: an LSDA+U study, Phys. Rev. B, 1998, 57, 1505-1509.         [ Links ]

23 A.J. Devey, R. Grau-Crespo and N.H. de Leeuw, Combined density functional theory and interatomic potential study of the bulk and surface structures and properties of the iron sulfide Mackinawite (FeS), J. Phys. Chem. C, 2008, 112, 10960-10967.         [ Links ]

24 A.J. Devey, R. Grau-Crespo and N.H. de Leeuw, Electronic and magnetic structure of Fe3S4: GGA+U investigation, Phys. Rev. B, 2009, 79, 195126.         [ Links ]

25 A. Devey and N.H. de Leeuw, Density functional theory study of the high- and low-temperature phases of cubic iron sulfide, Phys. Rev. B, 2010, 82, 235112.         [ Links ]

26 G. Kresse and J. Furthmüller, Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set, Phys. Rev. B, 1996, 54, 11169-11186.         [ Links ]

27 G. Kresse and J. Furthmüller, Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set, Comput. Mater. Sci., 1996, 6, 15-50.         [ Links ]

28 G. Kresse and J. Hafner, Ab initio molecular dynamics for open-shell transition metals, Phys. Rev. B, 1993, 48, 13115-13118.         [ Links ]

29 G. Kresse and J. Hafner, Norm-conserving and ultrasoft pseudo-potentials for first-row and transition elements, J. Phys. Condens. Matter, 1994, 6, 8245-8257.         [ Links ]

30 P. Hohenberg and W. Kohn, Inhomogeneous electron gas, Phys. Rev., 1964,136, B864-B871.         [ Links ]

31 J.P. Perdew, K. Burke and M. Ernzerhof, Generalized gradient approximation made simple, Phys. Rev. Lett., 1996, 77, 3865-3868.         [ Links ]

32 S. Grimme, J. Antony, S. Ehrlich and H. Krieg, A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu, J. Chem. Phys., 2010, 132, 154104.         [ Links ]

33 D. Santos-Carballal, A. Roldan, R. Grau-Crespo and N.H. de Leeuw, A DFT study of the structures, stabilities and redox behaviour of the major surfaces of magnetite Fe₃O₄, Phys. Chem. Chem. Phys., 2014,16, 21082-21097.         [ Links ]

34 A.E. Shields, D. Santos-Carballal and N.H. de Leeuw, A density functional theory study of uranium-doped thoria and uranium adatoms on the major surfaces of thorium dioxide, J. Nucl. Mater., 473, 2016, 99-111.         [ Links ]

35 C.E. Hernandez-Tamargo, A. Roldan, P.E. Ngoepe and N.H. de Leeuw, Periodic modeling ofzeolite Ti-LTA, J. Chem. Phys., 2017,147,074701.         [ Links ]

36 U. Terranova and N.H. de Leeuw, Aqueous Fe2S2 cluster: structure, magnetic coupling, and hydration behaviour from Hubbard U density functional theory, Phys. Chem. Chem. Phys., 2014, 16, 13426-13433.         [ Links ]

37 D. Santos-Carballal, A. Roldan and N.H. de Leeuw, Early oxidation processes on the Greigite Fe₃S₄(001) surface by water: a density functional theory study, J. Phys. Chem. C, 2016,120, 8616-8629.         [ Links ]

38 D. Santos-Carballal, A. Roldan, N.Y. Dzade and N.H. de Leeuw, Reactivity of CO₂ on the surfaces of magnetite (Fe₃O₄), greigite (Fe₃S₄) and mackinawite (FeS), Philos. Trans. R. Soc. A, Math. Phys. Eng. Sci., 2018, 376, 20170065.         [ Links ]

39 A. Cadi-Essadek, A. Roldan and N.H. de Leeuw, Ni Deposition on Yt-tria-stabilized ZrO₂(111) surfaces: a density functional theory study, J. Phys. Chem. C, 2015,119, 6581-6591.         [ Links ]

40 A. Cadi-Essadek, A. Roldan and N.H. de Leeuw, Density functional theory study of Ni clusters supported on the ZrO₂(111) Surface, Fuel Cells, 2017,17, 125-131.         [ Links ]

41 A. Cadi-Essadek, A. Roldan and N.H. de Leeuw, Density functional theory study of the interaction of H₂O, CO₂ and CO with the ZrO₂ (111), Ni/ZrO₂ (111), YSZ (111) and Ni/YSZ (111) surfaces, Surf. Sci., 2016, 653, 153-162.         [ Links ]

42 S.S. Tafreshi, A. Roldan and N.H. de Leeuw, Micro-kinetic simulations of the catalytic decomposition of hydrazine on the Cu(111) surface, Faraday Discuss., 2017,197, 41-57.         [ Links ]

43 A. Roldan and N.H. de Leeuw, Selective hydrogenation of CO on Fe₃S₄{111}: a computational study, Faraday Discuss., 2017,197,325-336.         [ Links ]

44 N.Y. Dzade and N.H. de Leeuw, Adsorption and desulfurization mechanism of thiophene on layered FeS (001), (011) and (111) surfaces: a DFT-D2 study, J. Phys. Chem. C, 2018, 122, 359-370.         [ Links ]

45 V.I. Anisimov, M.A. Korotin, J. Zaanen and O.K. Andersen, Spin bags, polarons, and impurity potentials in La₂-_xSr_xCuO₄ from first principles, Phys. Rev. Lett., 1992, 68, 345-348.         [ Links ]

46 P.E. Blöchl, Projector augmented-wave method, Phys. Rev. B, 1994,50, 17953-17979.         [ Links ]

47 V.A. de la Peña O'Shea, I.D.P.R. Moreira, A. Roldan and F. Illas, Electronic and magnetic structure of bulk cobalt: the a, ß, and e-phases from density functional theory calculations, J. Chem. Phys., 2010,133, 1-8.         [ Links ]

48 V.A. de la Peña O'Shea, P.R. De la Piscina, N. Homs, G. Aromí and J.L.G. Fierro, Development of hexagonal closed-packed cobalt nanoparticles stable at high temperature, Chem. Mater., 2009, 21, 5637-5643.         [ Links ]

49 H. Karaca, et al., Structure and catalytic performance of Pt-promoted alumina-supported cobalt catalysts under realistic conditions of Fischer-Tropsch synthesis, J. Catal., 2011, 277, 14-26.         [ Links ]

50 S. Lyu, et al., Role of active phase in Fischer-Tropsch synthesis: experimental evidence of CO activation over single-phase cobalt catalysts, ACS Catal., 2018, 8, 7787-7798.         [ Links ]

51 W.L. Roth, Magnetic structures of MnO, FeO, CoO, and NiO, Phys. Rev., 1958,110, 1333-1341.         [ Links ]

52 U.D. Wdowik and K. Parlinski, Lattice dynamics of CoO from first principles, Phys. Rev. B - Condens. Matter Mater. Phys., 2007, 75, 1-6.         [ Links ]

53 B.S. Youmbi and F. Calvayrac, Structure of CoO(001) surface from DFT + U calculations, Surf. Sci., 2014, 621, 1-6.         [ Links ]

54 M. Forti, P. Alonso, P. Gargano and G. Rubiolo, Transition metals monoxides. An LDA+U study, Procedia Mater. Sci., 2012,1, 230-234.         [ Links ]

55 W.L. Roth, The magnetic structure of Co₃O₄, J. Phys. Chem. Solids, 1964, 25, 1-10.         [ Links ]

56 S. Hautecler and D. Scheerlinck, Magnetic interactions in Co₃O₄, Phys. status. solidi. B, 1976, 73, 223-228.         [ Links ]

57 W. Kündig, M. Kobelt, H. Appel, G. Constabaris and R.H. Lindquist, Mössbauer studies of Co₃O₄ material and ultrafine particles, J. Phys. Chem. Solids, 1969, 30, 819-826.         [ Links ]

58 F. Ono and H. Maeta, Determination of lattice parameters in Hcp cobalt by using X-Ray bond's method, Le J. Phys. Colloq., 1988, 49, C8-63-C8-64.         [ Links ]

59 J. van Elp, et al., Electronic structure of CoO, Li-doped CoO, and LiCoO₂, Phys. Rev. B, 1991,44, 6090-6103.         [ Links ]

60 W. Jauch, M. Reehuis, H. Bleif and F. Kubanek, Crystallographic symmetry and magnetic structure of CoO, Phys. Rev. B, 2001, 64, 052102-1-3.         [ Links ]

61 M. Lenglet and B. Lefez, Infrared optical properties of cobalt (II) spinels, Solid State Commun., 1996, 98, 689-694.         [ Links ]

62 A. Schrön, C. Rödl and F. Bechstedt, Crystalline and magnetic aniso-tropy of the 3d-transition metal monoxides MnO, FeO, CoO, and NiO, Phys. Rev. B - Condens. Matter Mater. Phys., 2012, 86, 1-11.         [ Links ]

63 A. Roldan, D. Santos-Carballal and N.H. de Leeuw, A comparative DFT study of the mechanical and electronic properties of greigite Fe₃S₄ and magnetite Fe₃O₄, J. Chem. Phys., 2013, 138, 204712.         [ Links ]

64 S. Selcuk and A. Selloni, DFT+U study of the surface structure and stability of Co₃O₄(110): dependence on U, J. Phys. Chem. C, 2015,119, 9973-9979.         [ Links ]

65 C. Kittel and P. McEuen, Introduction to Solid State Physics, John Wiley & Sons, Hoboken, NJ, USA, 2019.         [ Links ]

66 H. Fujihisa and K. Takemura, Equation of state of cobalt up to 79 GPa, Phys. Rev. B, 1996, 54, 5-7.         [ Links ]

67 Y. Noguchi, T. Atou, T. Kondo, T. Yagi and Y. Syono, High-pressure phase transformation of cobalt monoxide due to electronic transition, Jpn. J. Appl. Phys., 1999, 38, L7-L9.         [ Links ]

68 S. Ohnishi and H. Mizutani, Crystal field effect on bulk moduli of transition metal oxides, J. Geophys. Res., 1978, 83, 1852-1856.         [ Links ]

69 L. Bai, et al., Charge transfer in spinel Co₃O₄ at high pressures, J. Phys. Condens. Matter, 2012, 24, 1-7.         [ Links ]

70 R. Gillen and J. Robertson, Accurate screened exchange band structures for the transition metal monoxides MnO, FeO, CoO and NiO, J. Phys. Condens. Matter, 2013, 25, 1-8.         [ Links ]

71 J. Chen, X. Wu and A. Selloni, Electronic structure and bonding properties of cobalt oxide in the spinel structure, Phys. Rev. B, 2011,83, 245204.         [ Links ]

72 D. Herrmann-Ronzaud, P. Burlet and J. Rossat-Mignod, Equivalent type-II magnetic structures: CoO, a collinear antiferromagnet, J. Phys. C: Solid State Phys., 1978,11, 2123-2137.         [ Links ]

73 E.Z. Kurmaev, et al., Oxygen x-ray emission and absorption spectra as a probe of the electronic structure of strongly correlated oxides, Phys. Rev. B - Condens. Matter Mater. Phys., 2008, 77, 1-5.         [ Links ]

74 V.R. Shinde, S.B. Mahadik, T.P. Gujar and C.D. Lokhande, Super-capacitive cobalt oxide (Co₃O₄) thin films by spray pyrolysis, Appl. Surf. Sci., 2006, 252, 7487-7492.         [ Links ]

75 V. Patil, Synthesis and characterization of Co₃O₄ thin film, Soft Nanosci. Lett., 2012, 2, 1-7.         [ Links ]

76 K.J. Kim and Y.R. Park, Optical investigation of charge-transfer transitions in spinel Co₃O₄, Solid State Commun., 2003,127, 25-28.         [ Links ]

77 C.-S. Cheng, M. Serizawa, H. Sakata and T. Hirayama, Electrical conductivity of Co₃O₄ films prepared by chemical vapour deposition, Mater. Chem. Phys., 1998, 53, 225-230.         [ Links ]

78 P. Wei and Z.Q. Qi, Insulating gap in the transition-metal oxides: a calculation using the local-spin-density approximation with the on-site Coulomb U correlation correction, Phys. Rev. B, 1994,49,864-868.         [ Links ]

79 X.B. Feng and N.M. Harrison, Electronic structure of MnO and CoO from the B3LYP hybrid density functional method, Phys. Rev. B-Condens. Matter Mater. Phys., 2004, 69, 1-7.         [ Links ]

80 V. Singh, M. Kosa, K. Majhi and D.T. Major, Putting DFT to the test: a first-principles study of electronic, magnetic, and optical properties of Co₃O₄, J. Chem. Theory Comput., 2015,11, 64-72.         [ Links ]

81 A. Walsh, et al., Structural, magnetic, and electronic properties of the Co-Fe-Al oxide spinel system: density-functional theory calculations, Phys. Rev. B, 2007, 76, 165119.         [ Links ]

82 L. Qiao, et al., Nature of the band gap and origin of the elec-tro-/photo-activity of Co₃O₄, J. Mater. Chem. C, 2013,1, 4628-4633.         [ Links ]

83 M.M. Waegele, H.Q. Doan and T. Cuk, Long-lived photoexcited carrier dynamics of d-d excitations in spinel ordered Co₃O₄, J. Phys. Chem. C, 2014,118, 3426-3432.         [ Links ]

84 A.F. Lima, Density functional theory study on the magnetic properties of Co₃O₄ with normal spinel structure, J. Phys. Chem. Solids, 2016, 91, 86-89.         [ Links ]

85 CRC Handbook of Chemistry and Physics, CRC, Boca Raton, FL, USA, and Taylor & Francis London [distributor], 2012.         [ Links ]

86 S. Chrétien and H. Metiu, Electronic structure of partially reduced rutile TiO2(110) surface: where are the unpaired electrons located? J. Phys. Chem. C, 2011,115, 4696-4705.         [ Links ]

87 Z.HuandH. Metiu, Choice of U for DFT+ U calculations for titanium oxides, J. Phys. Chem. C, 2011,115, 5841-5845.         [ Links ]

88 E. Finazzi, C. Di Valentin, G. Pacchioni and A. Selloni, Excess electron states in reduced bulk anatase TiO₂: comparison of standard GGA, GGA+U,andhybridDFTcalculations, J. Chem. Phys.,2008,129,1-9.         [ Links ]

89 J.J. Plata, A.M. Márquez and J.F. Sanz, Electron mobility via polaron hopping in bulk ceria: a first-principles study, J. Phys. Chem. C, 2013, 117, 14502-14509.         [ Links ]

90 X. Liu and C.T. Prewitt, High-temperature X-ray diffraction study of Co₃O₄: transition from mormal to disordered spinel, Phys. Chem. Miner., 1990,17, 168-172.         [ Links ]

91 S. Matar, A. Houari and A. Belkhir, Ab initio studies of magnetic properties of cobalt and tetracobalt nitride Co₄N, Phys. Rev. B, 2007,75,1-7.         [ Links ]

92 T. Archer, R. Hanafin and S. Sanvito, Magnetism of CoO polymorphs: density functional theory and Monte Carlo simulations, Phys. Rev. B-Condens. Matter Mater. Phys., 2008, 78, 1-5.         [ Links ]

93 H.X. Deng, et al., Origin of antiferromagnetism in CoO: a density functional theory study, Appl. Phys. Lett., 2010, 96, 162508-1-3.         [ Links ]

94 M.A. Langell, M.D. Anderson, G.A. Carson, L. Peng and S. Smith, Valence-band electronic structure of Co₃O₄ epitaxy on CoO(100), Phys. Rev. B, 1999, 59, 4791-4798.         [ Links ]

95 D. Santos-Carballal, A. Roldan, R. Grau-Crespo and N.H. de Leeuw, First-principles study of the inversion thermodynamics and electronic structure of FeM₂X₄ (thio)spinels (M = Cr, Mn, Co, Ni; X = O, S), Phys. Rev. B, 2015, 91, 195106.         [ Links ]

96 F.G. Kuang X.Y. Kuang S.Y. Kang and A.J. Mao, Magneto-elastic effects and thermodynamic properties of ferromagnetic hcp Co, Phys. B Condens. Matter, 2014, 441, 72-79.         [ Links ]

97 J.C. Crowhurst, et al., Determination of the high pressure elasticity of cobalt from measured interfacial acoustic wave velocities, Appl. Phys. Lett., 2006, 89, 1-3.         [ Links ]

98 G.Y. Guo and H.H. Wang, Gradient-corrected density functional calculation of elastic constants of Fe, Co and Ni in bcc, fcc and hcp structures, J. Magn. Magn. Mater., 2000, 38, 949-961.         [ Links ]

99 J. Sakurai, W.J.L. Buyers, R.A. Cowley and G. Dolling, Crystal dynamics and magnetic excitations in cobaltous oxide, Phys. Rev., 1968,167, 510-518.         [ Links ]

100 D. Antonangeli, et al., Elasticity of cobalt at high pressure studied by inelastic X-ray scattering, Phys. Rev. Lett., 2004, 93, 19-22.         [ Links ]

 

 

Received 22 January 2020
Revised 1 June 2020
Accepted 24 June 2020

 

 

* To whom correspondence should be addressed. E-mail: deleeuwn@cardlff.ac.uk
≠ Present address: School of Chemistry, University of Leeds, Leeds LS2 9JT, United Kingdom.