Services on Demand
Journal
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
SAIEE Africa Research Journal
On-line version ISSN 1991-1696Print version ISSN 0038-2221
SAIEE ARJ vol.109 n.3 Observatory, Johannesburg Sep. 2018
ARTICLE
Analysis of bounded distance decoding for Reed Solomon codes
O.P. Babalola; D.J.J. Versfeld
School of Electrical and Information Engineering,University of the Witwatersrand, Private Bag 3, Wits 2050, Johannesburg, South Africa. E-mail: 731200@students.wits.ac.za, and jaco.versfeld@wits.ac.za
ABSTRACT
Bounded distance decoding of Reed-Solomon codes involves finding a unique codeword if there is at least one codeword within the given distance. A corrupted message having errors that is less than or equal to half the minimum distance corresponds to a unique codeword and therefore, the probability of decoding error is one for a minimum distance decoder. However, increasing the decoding radius to be slightly higher than half of the minimum distance may result in multiple codewords within the Hamming sphere. In this study, we computed the probability of having unique codewords for (7, k) RS codes when the decoding radius is increased from the error correcting capability t to t +1. Simulation results show a significant effect of the code rates on the probability of having unique codewords. It also shows that the probability of having unique codeword for low rate codes is close to one.
Key words: Reed Solomon codes, Minimum distance decoder, Bounded distance decoding, Unique codeword, Hamming sphere.
1. INTRODUCTION
Reed-Solomon (RS) codes is a type of forward error correction (FEC) codes with several applications in storage systems, communications, spacecraft etc. In all practical error correction applications of RS codes, q is fixed to have a characteristics of 2, and the code symbols are over the Galois field GF(2m), where m is any positive integer. Bounded distance decoding (BDD) is based on sphere construction around each codeword [1]. The Hamming (decoding) sphere of a given radius t constructed about a codeword c has all vectors r at a Hamming distance less than or equal to the radius t from the codeword. If the Hamming spheres about each codeword have the same radius, the distance between two nearest codewords (dmin) in the code determines the largest radius creating nonoverlapping spheres. Figure 1 illustrates decoding spheres of radius t = [(dmin - 1)/2]. Whenever a vector r lies within a sphere around a codeword, the decoder assumes r is closer to the codeword in that particular sphere than to those in other spheres. The decoder therefore decodes r to the codeword inside the same sphere. Cheng and Wan [2] described the bounded distance decoding problem as finding a unique codeword if there is at least one codeword within a given distance, or produce an empty set if there is none. The best known bounded distance algorithm is the one proposed by Schmidt, Sidorenko, and Bossert (SSB) [3]. They considered a syndrome based approach in the frequency domain, which is used to decode RS codes beyond halfthe minimum distance. The maximum decoding radius is:


where l also dictates the rate restriction for increasing the decoding radius. SSB observed that for low rate codewords specified by (1), the probability of the bounded distance decoder's output containing only one codeword is very high, and therefore the BDD outputs the correctly decoded codeword. The decoder is allowed to fail with a small probability rather than having a list of solutions, while the technique was demonstrated to practically give the same decoding performance as the Sudan algorithm [4].
Based on the results in [3], we investigate the subset of BDD, where we decode up to t + 1 errors. A major contribution of this work is the computational analysis done to find the probability 'ρ' of obtaining a unique codeword when correcting up to t + 1 errors for short codes of length 7, which can be extended to longer length RS codes. This analysis significantly illustrates the underline issues with BDD whereby the algorithm fails to return a unique codeword for high rate codes. The rest of the paper is organized as follows. A basic description of the method used to analyze bounded distance decoding of RS codes is given in Section 2. Numerical analysis is done to examine (7, k) RS codes of different rates in Section 3. A performance comparison of the minimum distance decoding, and the bounded distance decoding is done in Section 4. Finally, Section 5. is a conclusion of the work done in this paper.
2. PROBABILITY OF OBTAINING UNIQUE CODEWORDS
The method of finding the probability of having unique codewords in the decoding radius of a (7, k) RS decoder includes; computing lookup tables, examining all (7,k) RS codes using the lookup table, and calculating probabilities of every k for w ≤ t and w ≤ t + 1 errors, where w is the actual number of errors added by the channel. To create a lookup table, all possible error vector combinations are generated with each row mapped to a syndrome vector. Also, to examine all (7, k) RS codes, the frequency of syndrome occurrences is checked to find the number of unique occurrences of each syndrome vector in the table. Thereafter, the probability of having unique codewords in the decoding radius of RS(7, k) codes is calculated as a ratio of the number of unique syndrome occurrences and syndrome possibilities. Each step is described as follows:
1. Column of possible error vectors: the number of possible error vectors from a field of q elements of length n and weight w,(w can be any field element apart from zero) is derived using the following combinatorial equation [5]:

where (q - 1)w is the number of error vectors, and
is the number of unordered selections of w error positions from a set of n positions. The total number of possible error vectors of weight from one to t is obtained as follows:

2. Column of possible syndrome vectors: The column contains corresponding possible syndrome vectors of length n - k. These vectors are obtained from the possible error vectors by evaluating value of each possible error vector at consecutive roots (α, α2,..., an-k) of the generator polynomial g( x) that generates the (7, k) RS code.
3. Column ofunique syndrome occurrence: In order to decode correctly, all possible syndromes must be disjoint [5]. Since the syndromes are obtained from corresponding combination of error vectors, there may be one or more syndromes that are repeated, and must therefore be examined for uniqueness. Unique Syndromes are obtained by searching through the column of possible syndrome vector and the number of time each syndrome occurs is observed. Syndromes with minimum occurrence of one are said to be unique, and placed in the column of unique syndrome occurrence in the lookup table.
4. Probability 'ρ': The probability of having unique codewords in decoding radius [t, t + 1] is obtained from the frequency of occurrence and possible syndrome vectors as given by the following equation:

Both cases of the minimum and bounded distance decoders of radius t and t + 1 respectively are examined. The results in both scenarios shows probabilities of having unique codewords for (7, k) RS codes.
3. NUMERICAL ANALYSIS FOR RS CODES OF DIFFERENT RATES
We now examine (7, k) RS codes of different code rates (k/n), where n = 7 and k = 2,3,4, and 5. We create the lookup tables, analyze the codes and calculate the probabilities of obtaining unique codewords of [t, t + 1] radius in both minimum and bounded distance decoders.
3.1 Minimum Distance Decoding for w ≤ t
Consider a t-error-correcting (7, k) RS code with symbols from GF'(23) generated by consecutive roots of a generator polynomial with degree (n - k). Assume the channel introduced w ≤ t errors to the transmitted message. Table 1 shows the analysis results for k = 4 and 5. There are 49 possible error vectors obtained using equation (2), and each error vector corresponds to a syndrome vector of length 3 and 2 respectively. Also, the frequency of syndrome occurrences from the column of possible syndromes (51) indicates all 49 syndromes in (51) occurred once.

The probability 'ρ' is given as

Table 2 is a result of analysis for k = 2 and 3. Here, the maximum error correcting capability t = 2, and all possible combination of error vectors with their corresponding possible syndrome vectors 51 are computed for w ≤ t errors. For w = 1, there are 49 possible syndrome vectors in 51 as shown in Table 1. For w = 2, the number of possible syndrome vectors becomes 1029, which implies 51 now contain a total of 1078 possible syndromes in the lookup table as shown in Table 2. The frequency of syndrome occurrences is checked in 51, where all 1078 syndromes occurred once; that is, the syndromes are all unique as shown in Table 2. The result of analysis is used to derive the probability of obtaining unique codeword in the given radius t as follows:

Figure 2 shows a relationship between the probabilities and message length k. The probabilities constantly gives one, which implies the minimum distance decoder always have unique codewords in the decoder's sphere. Hence, all error patterns w ≤ t are decoded correctly. The performance of minimum distance decoding for (7, k) RS codes with different rates is simulated and shown in Figure 3.


3.2 Bounded Distance Decoding for w ≤ t + 1
We assume the bounded distance decoder can correct more errors within the decoding radius t + 1. Therefore, analysis is performed to determine probabilities of having unique codewords within the BDD radius for (7,k) RS codes. First, we analyze both (7,5) and (7,4) RS codes. For a (7,5) RS code, suppose the channel introduces w = 1 error pattern, the lookup table contains 49 rows of possible error combinations with each row mapped to exactly 49 possible syndrome vector of length 2, in the column of possible syndrome vectors  . The frequency of syndrome occurrence is checked to determine the number of syndrome occurrences in
. The frequency of syndrome occurrence is checked to determine the number of syndrome occurrences in  , which yields all 49 syndromes in
, which yields all 49 syndromes in  occurring once, and are therefore unique syndromes. Furthermore, if the channel adds w = 2 error pattern, 1029 possible error combinations is obtained by (2). The column of possible syndrome vectors
occurring once, and are therefore unique syndromes. Furthermore, if the channel adds w = 2 error pattern, 1029 possible error combinations is obtained by (2). The column of possible syndrome vectors  containing 1029 syndromes is also obtained from corresponding error vectors. In this case, the lookup table now contains 1078 possible syndromes. This implies, some or all the 49 syndromes in
containing 1029 syndromes is also obtained from corresponding error vectors. In this case, the lookup table now contains 1078 possible syndromes. This implies, some or all the 49 syndromes in  may be repeated in
may be repeated in  and one or more syndromes in
and one or more syndromes in  may also occur more than once. Therefore, all the syndromes in
may also occur more than once. Therefore, all the syndromes in  must be checked for uniqueness. Table shows the frequency of syndrome occurrences and the number of unique syndromes in the lookup table. The probability of having unique codewords in the BDD of radius t + 1 is as follows:
must be checked for uniqueness. Table shows the frequency of syndrome occurrences and the number of unique syndromes in the lookup table. The probability of having unique codewords in the BDD of radius t + 1 is as follows:

The result of analysis for a (7,4) RS code is summarized in Table 4, which contains a total of 1078 possible syndrome vectors whereby 49 syndromes are unique in the lookup table. The probability of having unique codewords is also obtained as follows:

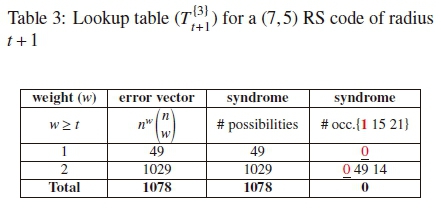

Comparing the frequency of syndrome occurrences in Tables and 4, it can be inferred that the BDD has more probability of decoding failure for a (7,5) RS code than a (7,4) RS code. This is because a (7,5) code has a minimum of 15 and maximum of 21 number of syndrome occurrences in contrast to a (7, 4) code that contains a minimum of 2 and maximum of 3 number of syndrome occurrences.
Next, we consider the low rate (7,3) and (7,2) RS codes. A similar lookup table is computed and used to obtain the probability of having unique codewords within the decoder's radius t + 1. For a (7,3) RS code, where the channel introduces error pattern of w ≤ t + 1. Assume w = 1, the lookup table  contains 49 rows of possible error combinations and corresponding rows of possible syndrome vector
contains 49 rows of possible error combinations and corresponding rows of possible syndrome vector  of length 4. The number of syndrome occurrence is examined, which yields all 49 syndromes occurring once. If w = 2, then the number of possible error vectors and corresponding syndrome vectors in
of length 4. The number of syndrome occurrence is examined, which yields all 49 syndromes occurring once. If w = 2, then the number of possible error vectors and corresponding syndrome vectors in  increases. From (2), there are 1029 possible combinations of error vectors mapped to corresponding syndrome vector rows,
increases. From (2), there are 1029 possible combinations of error vectors mapped to corresponding syndrome vector rows,  and when added to syndromes in
and when added to syndromes in  the number of syndrome rows to be examined for uniqueness in
the number of syndrome rows to be examined for uniqueness in  increases to 1078. The frequency of syndrome occurrence shows all 1029 syndromes from
increases to 1078. The frequency of syndrome occurrence shows all 1029 syndromes from  occurring without repetition, and are also independent of syndromes from
occurring without repetition, and are also independent of syndromes from  in this lookup table. Thus, all 1078 syndromes in
in this lookup table. Thus, all 1078 syndromes in  are unique. Suppose the channel introduces w = 3 errors, (2) gives 12005 possible error combinations, which has a one-to-one mapping with 12005 syndrome vector rows
are unique. Suppose the channel introduces w = 3 errors, (2) gives 12005 possible error combinations, which has a one-to-one mapping with 12005 syndrome vector rows  .
.  further increases to contain 13083 possible syndromes that must be checked for uniqueness. It is possible that some or all of the syndrome rows in
further increases to contain 13083 possible syndromes that must be checked for uniqueness. It is possible that some or all of the syndrome rows in  and
and  are contained in
are contained in  , while rows of
, while rows of  may also be repeated.
may also be repeated.
Table 5 shows the result of finding the frequency of syndrome occurrences in  which are disjoint of each other. The result indicates there are 49 unique syndromes in the lookup table, and the probability of having unique codewords is calculated as follows:
which are disjoint of each other. The result indicates there are 49 unique syndromes in the lookup table, and the probability of having unique codewords is calculated as follows:


From Table 6, it can be seen that for a (7,2) RS code, there are 49, 1029 and 11025 syndromes from disjoint vectors  which are unique in the lookup table
which are unique in the lookup table  .
.

The probability of having unique codewords in decoding radius t + 1 is obtained as

The frequency of syndrome occurrences in Tables 5 and 6 show a minimum of one and maximum of two number of syndrome occurrences for a (7, 2) codes as compared to a minimum of one and maximum of seven occurrences for a (7,3) code. There are also more unique syndromes for a (7,2) than a (7,3) RS code. Therefore, the BDD will perform better for a (7, 2) RS code.
4. PERFORMANCE COMPARISON OF THE MDD AND BDD FOR LOW RATE CODES
To verify how the bounded distance decoder performs for low rate codes (R < 1/3), a (7,2) RS code is simulated using both the minimum distance decoder that corrects t errors and the bounded distance decoder that corrects t + 1 errors. Figure 4 shows a relationship between the probability of obtaining unique codewords in radius t + 1 of a bounded distance decoder and dimension k of RS(7, k) codes, while Table 7 shows the maximum error correcting capability and the probability of having unique codewords for the MDD and BDD.


The simulation result in Figure 5, indicates that the bounded distance decoder performs better than the minimum distance decoder.

5. CONCLUSION
In this paper, we analyzed the case of (7, k) RS codes with decoding radius t, where the error value (w) is less than or equal to t. All the syndromes occurred uniquely in the lookup table, and the probabilities obtained for all code rates equals one. This is the case of minimum distance decoding where Peterson-Gorenstein-Zieler [6], Berlekamp-Massey [7], or the Extended Euclidean Algorithm [8] successfully decode all error patterns up to the designed radius t.
We have also been able to analyze the case where the error value (w) is less than or equal to t + 1; that is, a BDD of radius t + 1, which is the aim of this research. The probability obtained for a (7, 5) RS code indicates BDD of increased radius will always fail because it does not have any unique codewords. Similarly, a (7,4) RS code has a very low chance of correctly decoding error patterns containing values greater than t, due to the low probability of having unique codewords in the radius t + 1. For a (7,3) RS code, the probability of obtaining unique codewords tends to zero, therefore the BDD fails, while the probability obtained for a (7,2) RS code closely approach one, which implies the decoder will correct error patterns of error values greater than t, with very low probability of decoding failure. From the analysis in this work and simulation results, it can be concluded that the bounded distance decoder for low rate RS codes is capable of correcting error values greater than t, and specifically t + 1. Also, since Figure 4 indicates both (7, 4) and (7, 2) RS codes have a chance of performing better than (7, 5), and (7, 3) RS codes respectively, a further work can be done on RS code construction for bounded distance decoding of radius t + 1. Apart from construction, the BER performance of RS codes can be improved by combining the list of all possible codewords generated using the method in this study with soft-decision information.
ACKNOWLEDGEMENT
The financial support of the Centre for Telecommunication Access and Services (CeTAS), the University of the Witwatersrand, Johannesburg, South Africa is appreciated.
REFERENCES
[1] K. Moon Todd, Error Correction Coding - Mathematical Methods and Algorithms. New York Todd: John Wiley & Sons, 2005. [ Links ]
[2] Q. Cheng and D. Wan, "On the list and bounded distance decodability of Reed Solomon codes," Society for Industrial and Applied Mathematics, vol. 37, no. 1, pp. 195-209, 2007. [ Links ]
[3] G. Schmidt, V. R. Sidorenko, and M. Bossert, "Syndrome decoding of Reed-Solomon codes beyond half the minimum distance based on shift-register synthesis," in IEEE Transaction on Information Theory, vol. 56, no. 10, 2010, pp. 5245-5252. [ Links ]
[4] M. Sudan, "Decoding of Reed Solomon codes beyond the error-correction bound," in Journal of Complexity, vol. 13, no. 1, 1997, pp. 180-193. [ Links ]
[5] F. MacWilliams and N. Sloane, The Theory of Error-Correcting Codes, 3rd ed. North-Holland Publishing Company Amsterdam. New York. Oxford, 1981, vol. 16.
[6] W. W. Peterson., "Encoding and error-correction procedures for the Bose-Chaudhuri codes," IRE Transactions on Information Theory, vol. 6, no. 4, pp. 459-70, September 1960. [ Links ]
[7] E. R. Berlekamp, Algebraic Coding Theory: Revised Edition. Aegean Park Press,, 1984.
[8] S. Lin and D. J. Costello, Error Control Coding: Fundamentals and Applications. Saddle River, NJ 07458: Pearson Education Inc., Pearson Prentice Hall, 2004.













