Estimation of the additive and dominance variances in South African Landrace pigs

 

 

D. Norris^I, ; L. Varona^II; D.P. Visser^III; H.E. Theron^III; S.F. Voordewind^III; E.A. Nesamvuni^IV

^ISchool of Agricultural and Environmental Sciences, University of Limpopo, Private Bag X1106, Sovenga 0727, South Africa
^IICentre UDL-IRTA, Lleida 25198, Spain
^IIIARC-Animal Improvement Institute, Private Bag X2, Irene 0062, South Africa
^IVDepartment of Agriculture, Private Bag X9487, Polokwane 0700, South Africa

 

 

---

ABSTRACT

The objective of this study was to estimate dominance variance for number born alive (NBA), 21- day litter weight (LWT21) and interval between parities (FI) in South African Landrace pigs. A total of 26223 NBA, 21335 LWT21 and 16370 FI records were analysed. Bayesian analysis via Gibbs sampling was used to estimate variance components and genetic parameters were calculated from posterior distributions. Estimates of additive genetic variance were 0.669, 43.46 d² and 9.02 kg² for NBA, FI and LWT21, respectively. Corresponding estimates of dominance variance were 0.439, 123.68 d² and 2.52 kg², respectively. Dominance effects were important for NBA and FI. Permanent environmental effects were significant for FI and LWT21. It may be beneficial to evaluate non-additive genetic merit of individuals and families in addition to their transmitting abilities. A breeding program that capitalizes on non-additive genetic merit may be desirable.

Keywords: Non-additive genetic effects, Bayesian analysis, genetic parameters

---

 

 

Introduction

Quantitative genetic studies have shown that many traits under polygenic control harbour large amounts of additive genetic variation. It has also been observed in a number of studies that dominance genetic effects make significant contributions to phenotypic variation especially fitness and reproductive traits. Culbertson et al. (1998) showed estimates of dominance to be 25% and 78% of additive genetic variance for number born alive and 21 day litter weight respectively in Yorkshire pigs. Fuerst (1996) simulated a genetic model with different levels of additive, dominance and additive by additive genetic effects to assess the impact of dominance and epitasis on the genetic makeup of populations. The results showed that in the short term, rapid selection response could be achieved under the additive model while in the long term, more genetic gain could be achieved with the inclusion of non-additive genetic effects.

The key to detection of non-additive genetic effects lies in the familial structure of the data (Rye & Mao, 1996; Van Vleck & Gregory, 1996; Misztal, 1997). Populations that contain a large number of dominance relationships that are independent of additive genetic relationships, such as those arising from clones, full-sibs or three-quarter sibs, allow prediction of these effects. Pig populations which are litter-bearing species usually have a large number of non-additive relationships and therefore it may be important to determine the importance and magnitude of dominance genetic variance in pig populations. The objective of this study was therefore to estimate the dominance variance for reproductive and growth traits in the South African Landrace pigs.

 

Materials and Methods

The data was obtained from the South Africa National Pig Performance Testing Scheme of the Agricultural Research Council (ARC) - Animal Improvement Institute. A total of 26223 number born alive (NBA), 21335 litter weight at 21 days (LWT21) and 16370 farrowing interval (FI) records were analysed. The data sets were edited for connectedness and numerical outliers. Contemporary groups were determined by the National Pig Performance Testing Scheme of the ARC and were defined as a group of pigs farrowed, weaned and tested together under common management and environmental conditions. Contemporary groups were further edited to contain at least 10 sows from at least three different sires. There were 5625 sows and 1201 sires. The average full-sib family contained approximately three full-sibs. Phenotypic means and standard deviations are presented in Table 1.

 

 

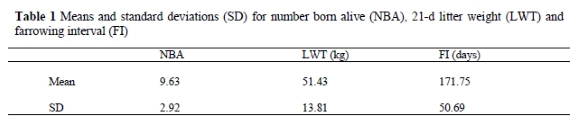
The three traits were analysed using the following repeatability model:

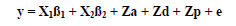
where y is the vector of records, ß₁ is the vector of contemporary group effects, ß₂ is the vector of parity effects, a is the vector of additive effects due to sows, d is the vector of dominance effects due to sows, p is the vector of animal permanent environmental effects and e is the vector of residuals. X and Z are matrices that relate records to their respective effects. Maternal effects were assumed non-existent. Inbreeding was found not significant in preliminary analyses and also not considered further.

It is assumed that vectors containing records on all traits are conditionally normally distributed as:

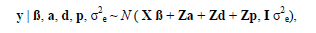
It is also assumed that additive, dominance and permanent effects are normally distributed.

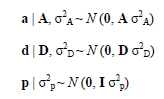
A has as elements, additive genetic relationships and D has dominance genetic relationships.

Estimates of variance components were obtained by Bayesian analysis procedures as described by Gelman et al. (1995), employing a Gibbs sampling algorithm as implemented by Jensen et al. (1994). The analysis was carried out considering one long chain with 225 000 samples assuming flat priors. Estimates were obtained as posterior means, disregarding the first 25 000 samples as burn-in. Thinning interval was 1 because maximum information was available with all samples, although the samples were correlated and not independent. The convergence was ensured using the algorithm of Raftery & Lewis (1992).

 

Results and Discussion

The means of the posterior distributions of estimates of variances for NBA, LWT21 and FI and their standard errors are presented in Table 2.

 

 

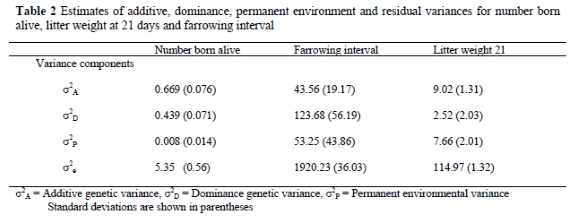
The additive genetic variances were larger than dominance and permanent environmental variances for NBA and LWT21. However, dominance effects seem to be significant for NBA. Dominance variance accounted for 66% of the additive genetic variance. For litter weight at 21 days, the dominance variance was 28% of the additive genetic variance. These findings are different from a study by Culbertson et al. (1998). In the Culbertson study, dominance in Yorkshire pigs was shown to be 25% and 78% of additive genetic variance for NBA and LWT21, respectively. Permanent environmental effects were not important for NBA but were 84% of the additive genetic variance for LWT21. Dominance genetic effects were large for FI. The dominance variance for this trait was three times larger than the additive variance. The permanent environmental variance was also larger than the additive genetic variance.

The results indicate that NBA and FI traits that can be considered as reproductive traits, were strongly affected by dominance effects. This is in agreement with several authors (Beckett et al., 1979; Philipsson, 1981; Hoeschele, 1991; Fuerst & Solkner, 1994) who indicated that non-additive genetic variance could be relatively important in fertility traits since these traits show low additive genetic variance.

Proportions of additive, dominance and permanent environment effects are shown in Table 3.

 

 

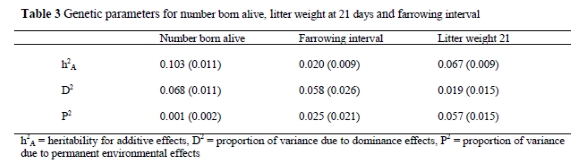
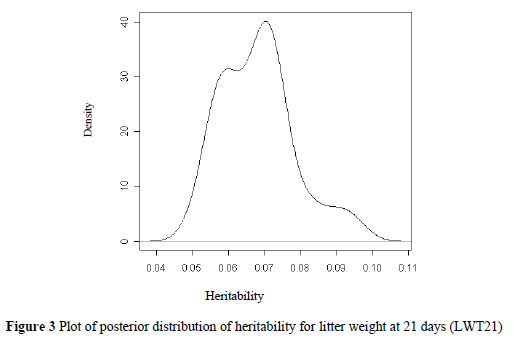
Plots of the posterior distributions of heritability for NBA, FI and LWT21 are shown in Figures 1, 2 and 3.

 

 

 

 

 

 

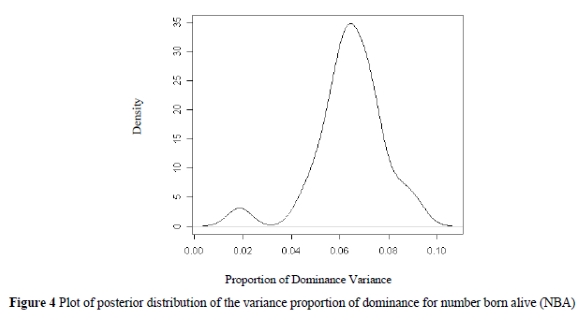
Plots of the posterior distributions of variance proportions of dominance for NBA, FI and LWT21 are shown in Figures 4, 5 and 6.

 

 

 

 

 

 

Heritability of additive effects for NBA is consistent with studies by Ferraz & Johnson (1993) and Skorupski et al. (1996), but slightly higher than values observed in other studies (Quijandria et al., 1983; Kaplon et al., 1991). It should be noted that the proportion of phenotypic variance accounted for by dominance effects for NBA was about two-thirds of the magnitude as heritability of additive effects for the same trait, indicating the importance of dominance effects in this trait. The heritability estimate of additive effects for LWT21 was lower than estimates observed in some studies (Quijandria et al., 1983; Ferraz & Johnson, 1993). However, a similar estimate was observed by Kaplon et al. (1991). It is interesting to note that this estimate (h²_A - LWT21) was lower than the estimate for NBA since it is generally accepted that heritability is higher for growth traits than fertility traits. The low estimate of heritability of additive effects for LWT21 seems to be due to the importance of permanent environmental effects on this trait. The permanent environmental effects were almost of equal magnitude to the additive effects for LWT21.

The proportion of phenotypic variance accounted for by dominance effects for farrowing interval was three times as large as the heritability of additive effects for this trait, indicating as already mentioned above the importance of dominance effects on this trait. The permanent environment effects were also important for this trait.

The standard errors were large for the observed estimates especially the dominance and permanent environment estimates. This could be due to the small data size. According to Chalh & Gazzah (2004), posterior means may not estimate variances efficiently with small data samples. According to Chang (1988), estimation of non-additive dominance effects requires large data sets. Misztal et al. (1998) suggested that accurate estimates of dominance variance require data sets with at least 30 000 to 100 000 animals for a population with many full-sibs. However, a simulation study by Norris et al. (2002) revealed that even when the data set is small, as long as the magnitude of the dominance genetic variance is large, dominance genetic variances can be estimated with relatively good accuracies.

Accuracy of genetic evaluations could be increased when dominance genetic effects are considered in the model of evaluation (Henderson, 1989; De Boer & Van Arendonk, 1992; Van Raden et al., 1992; Johansson et al., 1993; Misztal, 1997). Varona et al. (1998) found changes in breeding values when dominance effects were included in the evaluation model. Large breeding value differences were observed for dams with full-sib progeny. Accurate prediction of non-additive effects may be important in selection of mates based on their specific combining abilities (Jansen & Wilton, 1985; Destefano & Hoeschele, 1992). The present study did not look at what happens to the breeding values when the model of evaluation considers dominance effects and when the model does not. Future work will look into this.

 

Conclusion

The results suggest that dominance genetic effects affect expression of the traits studied. It may therefore be ideal to consider dominance effects for these traits in the genetic evaluation of pigs. These non-additive genetic effects may be exploited directly through specific mate allocation. Future work should determine whether the level of improvement in progeny merit is significantly higher when selecting for both additive and non-additive effects than in the current evaluation system which considers only the additive effects.

 

Acknowledgements

Financial assistance of National Research Foundation is gratefully acknowledged.

 

References

Beckett, R.C., Ludwick, E.R., Rader, E.R., Hines, H.C. & Pearson, R., 1979. Specific and general combining abilities for production and reproduction among lines of Holstein cattle. J. Dairy Sci. 62, 613-621.         [ Links ]

Chalh, A. & El Gazzah, M., 2004. Bayesian estimation of dominance merits in noninbred populations by using Gibbs sampling with two reduced sets of mixed model equations. J. Appl. Genet. 45, 331-339.         [ Links ]

Chang, H.A., 1988. Studies on estimation of genetic variances under nonadditive gene action. PhD thesis, University of Illinois, Urbana, USA.         [ Links ]

Culbertson, M.S., Mabry, J.W., Misztal, I., Gengler, N., Bertrand, J.K. & Varona, L., 1998. Estimation of dominance variance in purebred yorkshire swine. J. Anim. Sci. 76, 448-451.         [ Links ]

De Boer, I.J.M. & Van Arendonk, J.A.M., 1992. Prediction of additive and dominance effects in selected and unselected populations with inbreeding. Theor. Appl. Genet. 84, 451-459.         [ Links ]

Destefano, A.L. & Hoeschele, I., 1992. Utilization of dominance variance through mate allocation strategies. J. Dairy Sci. 75, 1680-1690.         [ Links ]

Ferraz, J.B.S. & Johnson, R.K., 1993. Animal model estimation of genetic parameters and response to selection for litter size and weight, growth and backfat in closed seed stock populations of Large White and Landrace swine. J. Anim. Sci. 71, 850-858.         [ Links ]

Fuerst, C., 1996. Impact of dominance and epistasis on the genetic makeup of simulated populations. J. Dairy Sci. 79 (Suppl. 1).         [ Links ]

Fuerst, C. & Sölkner, J., 1994. Additive and nonadditive genetic variances for milk yield, fertility and lifetime performance traits of dairy cattle. J. Dairy Sci. 77, 1114-1125.         [ Links ]

Gelman, A., Carlin, J. & Rubin, D., 1995. Bayesian Data Analysis. Chapman & Hall. London.         [ Links ]

Henderson, C.R., 1989. Prediction of merits of potential matings from sire-maternal grandsire models with nonadditive genetic effects. J. Dairy Sci. 72, 2592-2598.         [ Links ]

Hoeschele, I., 1991. Additive and nonadditive genetic variance in female fertility of Holsteins. J. Dairy Sci. 74, 1743-1752.         [ Links ]

Jansen, G.B. & Wilton, J.W., 1985. Selecting mating pairs with linear programming techniques. J. Dairy Sci. 68, 1302-1305.         [ Links ]

Jensen, J., Wang, C.S., Sorenson, D.A. & Gianola, D., 1994. Bayesian inference on variance and covariance components for traits influenced by maternal and direct genetic effects, using Gibbs Sampler. Acta Agric. Scand., Sect. A. Anim. Sci. 44, 193-201.         [ Links ]

Johansson, K., Kennedy, B.W. & Quinton, M., 1993. Prediction of breeding values and dominance effects from mixed models with approximations of the dominance relationship matrix. Livest. Prod. Sci. 34, 213-223.         [ Links ]

Kaplon, M.J., Rothschild, M.F., Berger, P.J. & Healey, M., 1991. Population parameter estimates for performance and reproductive traits in Polish Large White nucleus herds. J. Anim. Sci. 69, 91-98.         [ Links ]

Misztal, I., 1997. Estimation of variance components with large-scale dominance models. J. Dairy Sci. 80, 965-974.         [ Links ]

Misztal, I., Varona, L., Culbertson, M., Gengler, N., Bertrand, J.K., Mabry, J., Lawlor, T.J. & Van Tassell, C.P., 1998. Studies on the value of incorporating effect of dominance in genetic evaluations of dairy cattle, beef cattle and swine. Proc: 6^th World Con gress on Genetics Applied to Livestock. Australia, 1998.         [ Links ]

Norris, D., Mao, I.L. & Coetzee, R.J., 2002. Effect of population structure and underlying magnitude of dominance genetic effects on the estimation of additive and dominance genetic variances. S. Afr. J. Anim. Sci. 32, 353-357.         [ Links ]

Philipsson, J., 1981. Genetic aspects of female fertility in dairy cattle. Livest. Prod. Sci. 8, 307-319.         [ Links ]

Quijandria, B., Chauca de Zaldivar, L. & Robison, O.W., 1983. Selection in guinea pigs: I. Estimation of phenotypic and genetic parameters for litter size and body weight. J. Anim. Sci. 56, 814-819.         [ Links ]

Raftery, A.E. & Lewis, S.M., 1992. Bayesian Statistics. Oxford University Press, Oxford, U.K.         [ Links ]

Rye, M. & Mao, I.L., 1998. Nonadditive genetic effects and inbreeding depression for body weight in Atlantic salmon (Salmo salar L.). Livest. Prod. Sci. 57, 15-22.         [ Links ]

Skorupski, M.T., Garrick, D.J. & Blair, H.T., 1996. Estimates of genetic parameters for production and reproduction traits in three breeds of pigs. New Zealand J. Agric. Res. 39, 387-395.         [ Links ]

Van Raden, P.M., Lawlor, T.J., Short, T.H. & Hoeschele, I., 1992. Use of reproductive technology to estimate variances and predict effects of gene interactions. J. Dairy Sci. 75, 2892-2901.         [ Links ]

Van Vleck, L.D. & Gregory, K.E., 1996. Variances of additive and dominance genetic effects for ovulation and twinning rates in a population selected for twinning. J. Anim. Sci. 74, 1234-1239.         [ Links ]

Varona, L., Misztal, I., Bertrand, J.K. & Lawlor, T.J., 1998. Effect of full-sibs on additive breeding values under the dominance model for stature in United States Holstein. J. Dairy Sci. 81, 1126-1135.         [ Links ]

 

 

# Corresponding author. E-mail: norrisd@ul.ac.za