CONFERENCE PAPERS

 

Selective sublimation/desublimation separation of ZrF₄ and HfF₄

 

 

C.J. Postma^I; S.J. Lubbe^II; P.L. Crouse^II

^IThe South African Nuclear Energy Corporation SOC Ltd. (Necsa), Pretoria, South Africa
^IIDepartment of Chemical Engineering, University of Pretoria, South Africa

 

 

---

SYNOPSIS

The separation of zirconium and hafnium, which is essential in the nuclear industry, is difficult due to the great similarities in their chemical and physical properties. In contrast to the traditional aqueous chloride separation systems, the current process focuses on dry fluoride-based technologies, which produce much lower volumes of chemical waste. In the present work, separation is achieved in both a sublimation and a desublimation step, where the Zr/Hf mole ratio varies between 160 and 245 across the length of desublimer and 86 to 40 within the sublimer. Model predictions for the sublimation/desublimation rates fit the experimental results well, with deviations becoming more apparent as sublimation proceeds. This may be attributed to crust formation preventing the system from reaching thermodynamic equilibrium. The model adequately predicts time- and temperature-dependent mole ratios of both the sublimer residue and of the desublimed mass.

Keywords: zirconium, hafnium, fluoride, sublimation, desublimation.

---

 

 

Introduction

Zr ores typically contain between 1 and 3 wt.% Hf (Xu et al, 2012). Zr metal for use in the nuclear industry is required to have a Hf content <100 ppm, owing to its high neutron cross-section (Brown and Healy, 1978). Therefore, the separation step is crucial in the preparation of nuclear-grade Zr metal, but this is considered to be very difficult due to the close similarities in the chemical properties of Zr and Hf (Smolik, Jakóbik-Kolon and Poranski, 2009).

Generally, the preparation of Hf-free Zr relies on the traditional wet routes, for example solvent extraction systems (Banda, Lee and Lee., 2012; Brown and Healy, 1978; Deorkar and Khopkar, 1991; Taghizadeh, Ghanadi and Zolfonoun, 2011, 2008; Xu et al., 2012; Yang, Fane and Pin, 2002). In contrast to the traditional aqueous chloride systems, the dry processes have the advantage of producing much less hazardous chemical waste.

The New Metals Development Network (NMDN) under the Advanced Metals Initiative (AMI) was created by the Department of Science and Technology (DST) of South Africa in 2006, with the mandate to develop new processes for beneficiation relating to the elements Zr, Hf, Ta and Nb. The current work demonstrates an attempt to develop a process involving the beneficiation of the mineral zircon (ZrSiO₄) to produce nuclear-grade Zr metal. The zircon contains Hf as an impurity. To indicate this, the formula Zr(Hf)SiO₄ is used throughout this text. In the zircon crystal structure, Zr and Hf occur in identical crystallographic positions.

The proposed Zr metal recovery process involves plasma dissociation of the Zr(Hf)SiO4, which results in a much higher chemical reactivity. Here the zircon particles condense upon cooling as microcrystals of Zr(Hf)O2 embedded in an amorphous silica matrix, which is referred to as plasma-dissociated zircon (PDZ, i.e. Zr(Hf)O₂ SiO₂). The PDZ is then desilicated (DPDZ or Zr(Hf)O2) and fluorinated with ammonium bifluoride (ABF) to produce Zr(Hf)F₄. Separation of Hf from the Zr can be achieved using either the tetrafluoride or tetrachloride form, the latter of which will require an additional chlorination step. The next step is the plasma reduction of the tetrahalide to the metal and finally, purification of the metal powder by means of a high-temperature vacuum furnace (Nel et al., 2013; Retief et al., 2011). The nomenclature Zr(Hf)F₄ defines a ZrF4 crystal structure in which 1 to 3% of the Hf is substituted for Zr. ZrF4 and HfF4 behave differently in the vapour phase due to the differences in vapour pressure. This implies that HfF4 is thermodynamically more stable than ZrF4 at a specific temperature. It is therefore assumed that the ZrF4 will sublime separately from the HfF4 due to the differences in thermodynamic stability of the two compounds.

In this process, separation of ZrF₄ and HfF4 is achieved using sublimation followed by desublimation. The separation involves the sublimation of the tetrafluorides in an inert atmosphere under controlled conditions. The sublimed mass (at approx. 800°C) diffuses into nitrogen, which is then passed across a water-cooled desublimer (annulus) with the aim of desubliming the one metal fluoride in preference to the other. This implies that separation is achieved in both the sublimer and desublimer, due to differences in both the sublimation and desublimation rates. These rates depend on the vapour pressures at the respective temperatures as well as the concentration and/or partial pressure differences. The aim is for the sublimer residue to be Hf-rich and the desublimer content Zr-rich. Zr/Hf content is determined by means of ICP- OES analysis.

The aim is to establish experimental conditions, i.e. sublimation time, temperature and position on the desublimer that provide optimal separation conditions. These conditions must, however, be compatible with economic considerations, as higher temperatures and longer sublimation runs will entail higher operating costs. This work is a continuation of previous work (Postma, Niemand and Crouse, 2015) with the same sublimation model but based on a different sublimation and desublimation (water-cooled) system. A desublimation model as well as experimental work is also included and compared to modelling results.

 

Literature review

Sublimation is a general method used for the purification of ZrF₄ by removing most trace elements, e.g. Fe, Co, Ni and Cu (Abate and Wilhelm, 1951; Dai et al., 1992; Kotsar' et al., 2001; MacFarlane, Newman and Voelkel, 2002; Pastor and Robinson, 1986; Solov'ev and Malyutina, 2002a; Yeatts and Rainey, 1965). Sublimation methods for the separation of Zr and Hf have been reported in the literature, but these methods are all carried out under vacuum conditions (Monnahela et al., 2013; Solov'ev and Malyutina, 2002b).

In the work done by MacFarlane, Newman and Voelkel (2002) the area-dependant rate of sublimation of ZrF4 was calculated and a value of approximately 1.87 g.m-2.s-1 was obtained at 850 to 875°C. Ti, Esyutin and Scherbinin (1990a, 1990b) found that pure ZrF4 has a higher sublimation rate than industrial-grade ZrF4, which contains a degree of impurities. They concluded that this phenomenon might be due to the accumulation of low-volatile components in the near-surface layer of the sample, making diffusion and evaporation increasingly difficult, resulting in decreased sublimation flux. This led to the assumption that there might be a possibility of 'crust-formation' which could limit the sublimation rate to a certain extent.

In a study on the influence of layer height on the vacuum sublimation rate of ZrF4, it was concluded that the sublimation rate does not necessarily depend on the height of the sample in the sublimator (Ti, Esyutin and Scherbinin, 1990c). This led to the assumption that the sublimation rates are area-dependent only and sublimation does not take place from the bulk of the material. Figure 1 gives a range of vapour pressures obtained from the literature for both ZrF4 and HfF₄ at temperatures above 600°C (Benedict Pigford and Levi, 1981; Cantor et al., 1958; Koreneo et al., 1972; Sense et al., 1953, 1954).

 

 

Process description

The block flow diagram of the process is shown in Figure 2. The sublimation rates of ZrF4 and HfF4 are strongly dependent on the vapour pressures and the mole fraction of the respective components in the bulk mixture and therefore the sublimation rate of the ZrF4 is much higher than that of the HfF4. The aim is to exploit the difference in vapour pressure between the two compounds for separation and to sublime a mass of Zr(Hf)F₄ at a predetermined temperature for a predetermined time and to stop sublimation after the time has elapsed. The sublimed mass enters a desublimation zone in which the ZrF₄ and HfF₄ desublime at different rates. Separation is thus achieved in both the sublimer and the desublimer.

The sublimer residue as well as the desublimed mass was collected, weighed and analysed for Zr and Hf content to thereby establish the amount of sublimation/desublimation steps required to achieve nuclear grade purity.

Figure 3 gives a schematic of the sublimer and desublimer inside the tube furnace. The section above the sublimation pan facilitates the flow of nitrogen gas, which reduces the partial pressure of the ZrF₄ and HfF₄ and carries the tetrafluorides to the desublimer space.

The sublimer is a reactor boat (Figure 4) which is 100 mm long and 20 mm deep and can take a maximum of 80 g Zr(Hf)F₄. The Zr(Hf)F₄ to be sublimed is placed in the boat, which is positioned in the centre of the heating zone within the tube furnace.

 

 

The desublimer is a long cylindrical pipe (cooled to approx. 30°C) inside another insulated pipe which facilitates the carrying of the gas mixture. A simple geometry is selected for the desublimer to facilitate easy removal of the components at the end of the experiment. The desublimer temperature is much lower than that of the outer pipe walls, in order to prevent desublimation on the outer pipe wall. The spacing between the two pipes is minimal to reduce the diffusion path of the condensing particles.

 

Experimental procedure

The Zr(Hf)F₄ used in the experments was prepared by reacting Zr(Hf)O₂ (originating from zircon) with ABF. The tube oven was heated to the set temperature (between 700 and 850°C) before sample loading. Nitrogen was used as the carrier gas throughout all experiments at a mass flow rate of 0.3 kg/h. Two types of experiment were undertaken. The first set of experiments was performed in order to determine the rate of sublimation, including the extent of separation of the Zr and Hf in the sublimer residue. To this end, several sublimers, each containing 15 g sample mass, were loaded into the tube furnace for a pre-determined time, each sublimer being individually loaded one after the other at different residence times.The weight losses (mass sublimed) as well as the Zr/Hf mole ratios were determined from the sublimer residue. No desublimer was used in these experiments for the determination of the rate of sublimation.

In the second set of experiments, three sublimers each containing 15 g Zr(Hf)F₄ were loaded in the tube furnace for 30 minutes. The aim was to desublime as much as possible on the length of the desublimer to determine the Zr/Hf mole ratio as a function of the desublimer length. It is assumed that the sublimation conditions are the same for the respective sublimer samples.

The Zr/Hf mole ratios were determined by dissolving the Zr(Hf)F4 mixture in HF and determining the Zr and Hf contents by means of ICP-OES analysis.

 

Modelling

Mass Diffusion Coefficients

The diffusion coefficient can be estimated using the Lennard-Jones potential to evaluate the influence of the molecular forces between the molecules. This correlation (Equation [1]), also known as the Chapman-Enskog equation, holds for binary gas mixtures of nonpolar, nonreacting species (Perry and Green, 1997; Welty, 2001), which is the case for ZrF₄ and HfF4 in nitrogen.

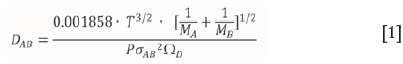
where σ_ABis the collision diameter, a Lennard-Jones parameter in Á, where A refers to nitrogen and B to either ZrF₄ or HfF₄. Since o is denoted as the Lennard-Jones diameter of the respective spherical molecule (Welty, 2001), an estimation was made for the diameter of a ZrF4 and HfF4 molecule assuming sphericity. The sizes of the respective molecules were calculated at room temperature with the use of Spartan^TMsoftware ('14 V1.1.4). The equilibrium geometry was calculated using the Hartree-Fock method with the 6-31* basis set. Estimated values for the collision diameters of ZrF4 and HfF4 with N2 were calculated as 4.205 and 4.185 Å, respectively.

The collision integral (Ώ_d) is a dimensionless parameter and a function of the Boltzmann constant (k), the temperature and the energy of molecular interaction ε_AB, where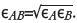 The boiling points (T_b for ZrF₄ (912°C) and HfF₄ (970°C) (Lide, 2007) were used to calculate the values for ε_B(molecular interaction of ZrF₄ or HfF₄) with the use of an empirical correlation, given by Equation [2]:

Estimated values for the energy of molecular interaction for ZrF₄ and HfF₄ in N₂ were calculated as 4.305 x 10^-14 and 4.409 x 10^-14 erg respectively.

Thermal Diffusion Coefficient

Kim (2013) demonstrated that the theoretical foundation of thermal diffusion relates to Einstein's random walk theory and added the spatial heterogeneity of the 'random walk' to reflect the temperature gradient of thermal diffusion. The thermal diffusivity was then determined theoretically. The walk speed S_wcorresponds to the speed of the Brownian particles, which is a function of temperature.

The molecular description of the thermal diffusion coefficient is given by:

which through integration yields (Nakashima and Takeyama, 1989; Kim, 2013):

Sublimation

The continuity equation in differential form is given by:

where p is the moles per unit volume (or area), j=(pū) is the flux, where u is the flow velocity vector field. S is the 'source' or 'sink' term, which is the generation per unit volume (or area) per unit time. In this case the source term is the sublimation rate (r_i).

The system is operated in such a way that no accumulation of mass occurs within the control volume 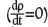, which implies that the net rate of mass efflux from the control volume equals the rate of sublimation. The continuity equation reduces to:

where i denotes either of the two species ZrF₄and HfF₄and r₁is the sublimation rate of ZrF₄ (or HfF₄) in moles per unit sublimation area per unit time. The rate model for the sublimation of ZrF4 and HfF4 is based on the work of Smith (2001), who predicted evaporation rates for liquid spills of chemical mixtures by employing vapour-liquid equilibrium. The sublimation rate is given by:

where ki is the mass transfer coefficient in m.s-1 at time t, P* is the vapour pressure in kPa, pi is the partial pressure in the bulk gas, xi is the mole fraction of ZrF₄ (or HfF₄) in the unsublimed bulk mass, R is the ideal gas constant (8.314 kPa.m3.kmol-1.K-1) and T is the temperature in K. Assuming that the flowing gas above the bed is homogenously mixed within each control volume, the net rate of mass efflux from the control volume can be written as follows:

The net rate of mass efflux from the control volume therefore reduces to:

In order to calculate the change in total flux along the length of the sublimation pan, the pan is divided into segments of length Δz and the flux in each successive segment is calculated by adding the flux in the previous segment to the sublimed masses of ZrF4 and HfF4 in segment j of length Az. The continuity equation therefore becomes:

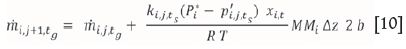
where mi,j+t_s is the total mass flow at time t of species i in the gas phase at the j^th position.

Desublimation

There are three 'mechanical driving forces' that tend to produce movement of a species with respect to the mean fluid motion. These are concentration gradient, pressure gradient and the external forces acting on the species. For purposes of this study, the assumption will be made that the effects of pressure gradient and external forces are negligible (Bird, Stewart and Lightfoot, 1960: 564-565). Therefore the diffusion currents consists of both density (Fick's Law) and temperature gradients (Ludwig-Soret effect). This macroscopic description of thermodiffusion dates back to the 19^th century and was developed in the context of standard kinetic theory and therefore applies to dilute gas mixtures only (Debbasch and Rivet, 2011). The mass flux can therefore be defined by two terms: (a) that of the concentration gradient, i.e. the concentration contribution to mass flux:

and (b) the temperature gradient, i.e. the thermal diffusion contribution to mass flux:

Di,N2 (previously defined as Dab) is the mass diffusion constant (m².s-i) of the diffusing species i in nitrogen, p is the density of the bulk gas (kg.m-³), mi is the mass fraction of the diffusion species, Di^Tis the thermal diffusion coefficient (a measure of the mass diffusion process due to temperature) and T the temperature (Bird et al., 1960: 502; Dominguez et al., 2011; Kim, 2013).

The thermal diffusion term (Ji^T) describes the tendency for species to diffuse under the influence of a temperature gradient. The species move toward colder regions and a concentration gradient is formed. The effect is small, but separations of mixtures can be effected with steep temperature gradients (Bird, Stewart and Lightfoot, 1960: 567; Kim, 2013).

The total mass flux equation can now be written as:

It is assumed that and that and therefore:

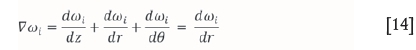
The same applies for the temperature change, where it is assumed that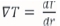

The total mass flux equation now reduces to:

The concentration contribution to mass flux (Ja⁽ⁱ⁾) can therefore be written as:

where ki^wis the mass transfer coefficient in the desublimer which is a function of the mass diffusivity and the film thickness, p´j,b is the partial pressure of species A in the bulk gas, p*i, w is the vapour pressure at the wall temperature and Tf is the film temperature, which is the average of the bulk and wall temperature. The temperature contribution to mass flux can therefore also be written as a function of the mass transfer coefficient:

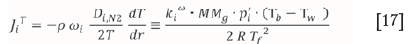
In order to calculate the change in total flux along the length of the desublimer (annulus), the length is divided into segments of length Az and the flux in each following segment is calculated by subtracting the desublimed masses of ZrF4 and HfF4 in the segment from the flux in the previous segment. The incremental mass balance in the desublimer along the length of the annulus can therefore be expressed by the following equation:

 

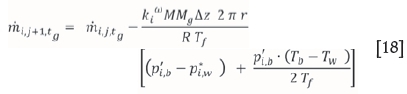
Results and discussion

Rate of Sublimation

The weight fraction sublimed at different temperatures are reported in Figure 5. These rates are calculated based on the sublimer residue, with zircon content subtracted.

 

 

One explanation for the sublimation rate forming a plateau before complete sublimation has been achieved (Figure 5) can be the formation of a crust-like surface or sintered cake (Figure 6) preventing further sublimation from occurring. This may be due to the presence of impurities originating from the zircon. The sublimation temperature stays the same, but sintering of the cake negatively influences the sublimation kinetics.

 

 

The modelled rates are shown in Figure 7 and compared to the linear sections of the sublimation rates obtained experimentally (Figure 5). The model accurately predicts the rates of sublimation at the lower temperatures, but seems to over-predict at the higher temperature of 790°C by a factor of 1.4.

 

 

This over-prediction of the sublimation rate at 790°C may be even greater at higher temperatures. For instance, the model predicts an average total flux of 7.34 g.m^-2.s^-1 for ZrF4 and HfF4 subliming at 850°C. This predicted value is 3.9 times higher than the 1.87 g.m^-2.s^-1 value estimated from results by MacFarlane, Newman and Voelkel (2002). One reason for the area-dependent rates differing might be the presence of impurities in the sample, since this can have a direct influence on the rate of sublimation (Ti, Esyutin and Scherbinin, 1990b). With the model, the effect of impurities on the rate is not taken into account, which will result in a higher sublimation rate.

Separation within the sublimer

Zr/Hf mole ratios for the sublimer residue ranged between 86:1 (starting material) and 30:1, depending on the sublimation temperature and duration. From Figure 8 it is evident that the sublimer residue becomes Hf-rich with time because HfF4 sublimes at a lower rate than ZrF4, which is mainly due to the lower sublimation temperature of the HfF4.

 

 

Comparison of the linear section of the experimental Zr/Hf mole ratio data with that obtained from the model indicates that the model predicts too high a sublimation rate for HfF4, resulting in lower Zr/Hf mole ratios in the sublimer residue. One explanation may be that the vapour pressure data for HfF₄ (only one source found in literature) is possibly wrong, which is likely due to the strong dependency of the vapour pressure on temperature, especially at high temperatures. The vapour pressure data for ZrF4 was taken from four sources with a standard error of 48.2 and 0.055 for the constants A and B in the vapour pressure correlation.

Desublimer

It is assumed that the sublimed ZrF₄ and HfF₄ desublimes into a crystal structure in which the Zr and Hf occur in identical crystallographic positions, as with the starting material. The mass desublimed on the desublimer is sampled at several intervals to determine whether the Zr/Hf ratio changes along the length of the desublimer. Figure 9 gives an illustration of the desublimer with desublimed Zr(Hf)F₄ and the respective sampling points.

 

 

Here X₀ is the tip of the desublimer closest to the heating zone and along the length of the desublimer are X₁ through to X5 which are 100 mm apart, with X1 being the first 10 mm on the desublimer. The sublimation temperatures investigated included 700, 740 and 790°C. Figure 10a gives an indication of separations achieved along the length of the desublimer. Figure 10b gives the Zr/Hf mole ratio of the collective mass obtained on the desublimer throughout.

It is clear that the sublimation temperature does have an effect on the separation achieved in the desublimer. Model predictions are not shown here, but indicate better separation with mole ratios typically higher by a factor of 1.5 at 700 and 740°C and 1.2 at 790°C. There is currently no explanation for this. A lower sublimation temperature will result in better separation. Separation is further achieved along the length of the desublimer, which may be helpful in the design of a large-scale desublimer with different product collection points along the length. At 700 and 740°C approximately 50% of the sublimed mass desublimed and 70% of the sublimed mass desublimed at 790°C. The reason for this is still unknown. One explanation might be the concentration in the bulk gas stream, which is higher at the higher temperature.

Number of Sublimation Steps Determined by the Model

Work reported in this paper is based on only a first sublimation step. This implies that the mass collected from the desublimer was not sublimed to account for a second or third step. The masses collected are simply too small to enable us to do second, third and so forth sublimation steps. The results collected from this first sublimation step were compared to the model and the comparisons used to estimate the extent of separation for second, third etc. sublimation steps. This is therefore a theoretical study to determine the number of sublimation steps required to achieve < 100 ppm Hf in the product. The model was run at a sublimation temperature of 790°C for several repetitions, each time entering a new value for the Hf concentration (i.e. HfF₄) in the bulk material with the assumption of removing the sublimer after 30 minutes. The Hf content calculated after each step was multiplied by 1.2 to account for inaccuracies in the model at this temperature. The assumption of 1.2 was incorporated since the model predictions deviated by a factor of 1.2 from the desublimation experimental results (i.e. Zr/Hf mole ratios).

The results obtained (Figure 11) indicated that eight steps are required to reduce the Hf concentration to less than 100 ppm. With the assumption of a 70% collection efficiency as found in the desublimation experimental results at 790°C, it is calculated that 15.5 kg would be required to produce 1 kg of nuclear-grade ZrF4.

 

 

There are many other factors that might influence the results, for example the particle surface area before and after sublimation and the amount of oxyfluorides present after collection from the desublimer. Also note that lower sublimation temperatures give better separation, but require longer sublimation times to achieve the same amount of sublimed material.

 

Conclusions

The sublimation and desublimation model sufficiently predicts the sublimation rates as well as the separation of the ZrF4 and HfF4 in both the sublimer and the desublimer. Optimal temperature selection for sublimation is imperative, since lower temperatures result in a lower sublimation rate but give better separation, whereas higher temperatures require shorter residence times but give slightly less separation of the two respective components. Based on several assumptions, the model was used with a sublimation temperature of 790°C and a residence time of 30 minutes. The model results indicated that eight steps are required to reduce the Hf concentration to less than 100 ppm.

 

Acknowledgements

The authors acknowledge the AMI of the DST and Necsa for providing the necessary funding and support to complete this study.

 

References

Abate, L.J. and Wilhelm, H.A. 1951. Sublimation of zirconium tetrafluoride. No. ISC-151. US Atomic Energy Commission, Ames Laboratory.         [ Links ]

Banda, R., Lee, H.Y. and Lee, M.S. 2012. Separation of Zr from Hf in hydrochloric acid solution using amine-based extractants. Industrial and Engineering Chemistry Research, vol. 51, no. 28. pp. 9652-9660.         [ Links ]

Benedict, M., Pigford, T.H. and Levi, H.W. 1981. Nuclear Chemical Engineering. McGraw-Hill.         [ Links ]

Bird, R.B., Stewart, W.E. and Lightfoot, E.N. 1960. Transport Phenomena. Wiley.         [ Links ]

Brown, A.E.P. and Healy, T.V. 1978. Separation of zirconium from hafnium in nitric acid solutions by solvent extraction using dibutyl butylphosphonate: Part 1. Chemistry of the separation. Hydrometallurgy, vol. 3, no. 3. pp. 265-274.         [ Links ]

Cantor, S., Newton, R., Grimes, W. and Blankenship, F. 1958. Vapor pressures and derived thermodynamic information for the system Rbf-ZrF₄. Journal of Physical Chemistry, vol. 62, no. 1. pp. 96-99.         [ Links ]

Dai, G., Huang, J., Cheng, J., Zhang, C., Dong, G. and Wang, K. 1992. A new preparation route for high-purity ZrF₄. Journal of Non-Crystalline Solids, vol. 140, nos. 1-3. pp. 229-232.         [ Links ]

Debbasch, F. and Rivet, J.P. 2011 .The Ludwig-Soret effect and stochastic processes. Journal of Chemical Thermodynamics, vol. 43, no. 3. pp. 300-306.         [ Links ]

Deorkar, N.V. and Khopkar, S.M. 1991. Liquid-liquid extraction of zirconium from hafnium and other elements with dicyclohexyl-18-crown-6. Analytica Chimica Acta, vol. 245. pp. 27-33.         [ Links ]

Dominguez, G., Wilkins, G. and Thiemens, M.H. 2011. The Soret effect and isotopic fractionation in high-temperature silicate melts. Nature, vol. 473 (7345). pp. 70-73.         [ Links ]

Kim, Y.J. 2013. Einstein's random walk and thermal diffusion. https://arxiv.org/abs/1307.4460 [accessed 12 May 2016].         [ Links ]

Koreneo, Y., Sorokin, I., Chirina, N. and Novoselo, A.V. 1972. Vapor-pressure of hafnium tetrafluoride. Zhurnal Neorganicheskoj Khimii, vol. 17, no. 5. p. 1195.         [ Links ]

Kotsar', M.L., Bateev, V.B., Baskov, P.B., Sakharov, V.V., Fedorov, V.D. and Shatalov, V.V. 2001. Preparation of high-purity ZrF₄ and HfF₄ for optical fibers and radiation-resistant glasses. Inorganic Materials, vol. 37, no. 10). pp. 1085-1091.         [ Links ]

Lide, D.R. 2007. CRC Handbook of Chemistry and Physics, 88th edn. CRC Press, London.         [ Links ]

MacFarlane, D.R., Newman, P.J. and Voelkel, A. 2002 Methods of purification of zirconium tetrafluoride for fluorozirconate glass. Journal of the American Ceramic Society, vol. 85, no. 6. pp. 1610-1612.         [ Links ]

Monnahela, O.S., Augustyn, W.G., Nel, J.T., Pretorius, C.J. and Wagener, J.B. 2013. The vacuum sublimation separation of zirconium and hafnium tetrafluoride. Proceedings of the AMI Precious Metals 2013 Conference, Protea Hotel, Cape Town, 14-16 October 2013. Southern African Institute of Mining and Metallurgy, Johannesburg.         [ Links ]

Nakashima, K. and Takeyama, N. 1989. Thermal diffusion in a Lorentz gas. Journal of the Physical Society of Japan, vol. 58, no. 12. pp. 4352-4357.         [ Links ]

Nel, J.T., Havenga, J.L., du Plessis, W. and Le Roux, J.P. 2013. Treatment of chemical feedstocks. uS patent 9468975 B2.         [ Links ]

Pastor, R.C. and Robinson, M. 1986. Method for preparing ultra-pure zirconium and hafnium tetrafluorides. uS patent 4578252 A.         [ Links ]

Perry, R.H. and Green, D.W. 1997. Perry's Chemical Engineers' Handbook. 7th Edition, McGraw-Hill, New York.         [ Links ]

Postma, J.J., Niemand, H.F. and Crouse P.L. 2015. A theoretical approach to the sublimation separation of zirconium and hafnium in the tetrafluoride form. Journal of the Southern African Institute of Mining and Metallurgy, vol. 115, no. 10. pp. 961-965.         [ Links ]

Retef, W.L., Nel, J.T., du Plessis, W. and Crouse, P.L. 2011. Treatment of zirconia-based material with ammonium bi-fluoride. US patent 8778291 B2.         [ Links ]

Sense, K.A., Snyder, M.J. and Clegg, J.W. 1953. Vapor pressures of beryllium fluoride and zirconium fluoride. US Atomic Energy Commission Technical Information Services, Oak Ridge, Tennessee.         [ Links ]

Sense, K.A., Snyder, M.J. and Filbert, R.B.J. 1954. The vapor pressure of zirconium fluoride. Journal of Physical Chemistry, vol. 58, no. 11. pp. 995-996.         [ Links ]

Smith, R.L. 2001. Predicting evaporation rates and times for spills of chemical mixtures. Annals of Occupational Hygiene, vol. 45. pp. 437-445.         [ Links ]

Smolik, M., Jakóbik-Kolon, A. and Poraski, M. 2009. Separation of zirconium and hafnium using Diphonix® chelating ion-exchange resin. Hydrometallurgy, vol. 95, nos. 3-4. pp. 350-353.         [ Links ]

Solov'ev, A.I. and Malyutina, V.M. 2002a. Metallurgy of less-common and precious metals. Production of metallurgical semiproduct from zircon concentrate for use in production of plastic metallic zirconium. Russian Journal of Non-Ferrous Metals, vol. 43, no. 9. pp. 9-13.         [ Links ]

Solov'ev, A.I. and Malyutina, V.M. 2002b. Production of metallic zirconium tetrafluoride purified from hafnium to reactor purity. Russian Journal of Non-Ferrous Metals, 43 (9). pp. 14-18.         [ Links ]

Taghizadeh, M., Ghanadi, M. and Zolfonoun, E. 2011. Separation of zirconium and hafnium by solvent extraction using mixture of TBP and Cyanex 923. Journal of Nuclear Materials, vol. 412, no. 3. pp. 334-337.         [ Links ]

Taghizadeh, M., Ghasemzadeh, R., Ashrafizadeh, S.N., Saberyan, K. and Maragheh, M.G. 2008. Determination of optimum process conditions for the extraction and separation of zirconium and hafnium by solvent extraction. Hydrometallurgy, vol. 90, nos. 2-4. pp. 115-120.         [ Links ]

Ti, V.A., Esyutin, V.S. and Scherbinin, V.P. 1990a. The dependence of the zirconium tetrafluoride sublimation rate upon the process pressure. Kompleksnoe Ispol'zovanie Mineral'nogo Syr'ya, vol. 10. pp. 61-63.         [ Links ]

Ti, V.A., Esyutin, V.S. and Scherbinin, V.P. 1990b. The dependence of the zirconium tetrafluoride sublimation rate in vacuum upon the process temperature and product composition. Kompleksnoe Ispol'zovanie Mineral'nogo Syr'ya, vol. 9. pp. 63-64.         [ Links ]

Ti, V.A., Esyutin, V.S. and Scherbinin, V.P. 1990c. The influence of the sample height on the zirconium tetrafluoride sublimation process. Kompleksnoe Ispol'zovanie Mineral'nogo Syr'ya, vol. 8. pp. 60-61.         [ Links ]

Welty, J.R., Wicks, C.E., Wilson, R.E. and Rorrer, G. 2001. Fundamentals of Momentum, Heat and Mass Transfer. Wiley, New York.         [ Links ]

Xu, Z., Wang, L., Wu, Y., Chi, R., Zhang, L. and Wu, M. 2012. Solvent extraction of hafnium from thiocyanic acid medium in DIBK-TBP mixed system. Transactions of Nonferrous Metals Society of China, vol. 22, no. 7. pp. 1760-1765.         [ Links ]

Yeatts, L.B. and Rainey, W.T. 1965. Purification of zirconium tetrafluoride. Technical report ORNL-TM-1292, US Atomic Energy Commission.         [ Links ]

Yang, X.J., Fane, A.G. and Pin, C. 2002. Separation of zirconium and hafnium using hollow fibers: Part i. Supported liquid membranes. Chemical Engineering Journal, vol. 8, nos. 1-3. pp. 37-44.         [ Links ] ♦

 

 

This paper was first presented at the AMI Precious Metals 2017 Conference 'The Precious Metals Development Network' 17-20 October 2017, Protea Hotel Ranch Resort, Polokwane, South Africa.