Services on Demand
Journal
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
Journal of the Southern African Institute of Mining and Metallurgy
On-line version ISSN 2411-9717Print version ISSN 2225-6253
J. S. Afr. Inst. Min. Metall. vol.121 n.9 Johannesburg Sep. 2021
https://doi.org/10.17159/2411-9717/522/2021
PAPERS OF GENERAL INTEREST
Truck dispatching in surface mines -Application of fuzzy linear programming
A. Moradi-AfrapoliI; S. UpadhyayII; H. Askari-NasabI
IMining Optimization Laboratory (MOL), School of Mining Engineering, Department of Civil and Environmental Engineering, University of Alberta, Canada. A. Afrapoli: https://orcid.org/0000-0002-2659-0112
IICanadian Natural Resources Limited (CNRL), Calgary, Canada
SYNOPSIS
Material handling in surface mines accounts for around 50% of the operational cost. Optimum truck dispatching plays a critical role in the reduction of this operational cost in truck and shovel surface mines. Researchers in this field have presented several mathematical models to solve the truck dispatching problem optimally. However, a critical survey of the literature has shown that three significant drawbacks exist in the available truck dispatching models. The published models underestimate the importance of the interaction between truck fleet, shovel fleet, and the processing plants. They also disregard goals set by strategic-level plans. Moreover, none of the available models account for the uncertainty associated with the input parameters. In this paper we present a new truck dispatching model that covers all of these drawbacks, using a fuzzy linear programming method. The performance of the developed model was evaluated through implementatin in an active surface mining operation. The results show a significant improvement in production and fleet utilization.
Keywords: Truck dispatching problem, fuzzy linear programming, surface mining, simulation, truck and shovel, material handling.
Introduction
As mining operations involve expenditures of millions or billions of dollars, cutting their costs by even two or three per cent will result in considerable savings for the stakeholders. In truck and shovel surface mining operations, material handling accounts for 50 to 60% of the total operating costs (Alarie and Gamache, 2002; Oraee and Goodarzi, 2007; Akbari, Osanloo and Shirazi, 2009; Upadhyay and Askari-Nasab, 2016; Moradi Afrapoli and Askari-Nasab, 2019). Thus, improving the performance of the material handling system and subsequently reducing its operating costs would result in significant savings. One of the several existing ways to improve the performance of material handling systems in truck and shovel surface mining operations is to make optimal decisions for truck allocation and dispatching. In this paper, we present a decision-making model that makes optimal decisions for truck dispatching in truck and shovel surface mines.
In the truck dispatching problem, decision-making models dispatch the 'best' trucks to the 'neediest' shovels. Definition of the best trucks and the neediest shovels can be found in Olson, Vohnout, and White (1993) and Temeng, Otuonye, and Frendewey (1998). Several models to solve the truck dispatching problem have been developed since the 1970s. However, the models published thus far have three limitations, which lead to non-optimal dispatching of trucks. The existing truck dispatching models usually omit the truck fleet, shovel fleet, or the processing plant from their calculations. Furthermore, the available models either ignore the production target that is set by the strategic plans or incorporate it as a soft constraint. The published models also disregard the stochastic behaviour of the input parameters.
This paper aims to introduce a new mathematical model to solve the truck dispatching problem in surface mines. Our model assigns equal weights to the impact of the truck fleet, shovel fleet, and processing plant in the truck dispatching process. Our developed model also applies fuzzy linear programming (FLP) to incorporate the imprecision of the input parameters in the solution procedure. We implemented our model in a real case study, using the study's site's in-place fleet management system, which is the backbone algorithm of Modular Mining DISPATCH® (Modular Mining Systems Inc., 2020), as the benchmark to evaluate the model performance.
Literature
Mining researchers have developed several decision-making tools for optimizing truck dispatching decisions in the last 50 years. The models thus far developed are categorized into two main classes - the single-stage and the multi-stage truck dispatching models (Alarie and Gamache; 2002; Moradi Afrapoli and Askari-Nasab, 2019).
The single-stage models make two simultaneous decisions. They simultaneously decide on the required flow rate along paths between shovels and dumps and dispatching of the trucks to shovels. The truck dispatching model developed by Hauck (1973) is categorized in the single-stage class.
The multi-stage models divide the truck dispatching problem into two sub-problems. In the first sub-problem, a mathematical model determines the rate of production for each path between shovels and dumps (truck allocation). This step is called the upper stage (Alarie and Gamache, 2002). Most of the literature related to truck allocation and dispatching problems deals with developing a decision-making model to solve the upper stage sub-problem. A detailed review of the latest published models to address the upper stage problem can be found in Moradi Afrapoli and Askari-Nasab (2019).
In the second sub-problem, a mathematical model makes decisions on the next destination of the trucks (truck dispatching). This step is called the lower stage (Alarie and Gamache, 2002). There are only a few published models in the literature that make the lower stage decisions. White and Olson (1986) and Olson, Vohnout, and White (1993) presented a truck dispatching model based on dynamic programming. Their model creates a list of available trucks and a list of active shovels. Then, based on a 1-truck-m-shovel approach (Alarie and Gamache, 2002) it dispatches the best truck to the right shovel.
Soumis, Ethier, and Elbrond (1989) developed a truck dispatching model that solves the lower stage sub-problem using a model based on the classical assignment problem approach. The model considers the next 10 to 15 trucks that need a new assignment.
Li (1990) presented a truck dispatching model that dispatches trucks based on a maximum inter-truck-time dispatching rule. An empty truck is sent to the shovel at which the difference between actual inter-truck time and the optimal inter-truck time is the greatest.
Temeng, Otuonye, and Frendewey (1997) presented a truck dispatching model based on the analogy of the transportation problem approach. Their proposed model can be implemented in a mine where a heterogeneous truck fleet is used for material transportation. Their model also considers the situation in which a shovel is far behind its target production and needs to be assigned more than one truck. In such a case, the model efficiently assigns more than a single truck to those shovels that are further behind their schedule.
Recently, Moradi-Afrapoli, Tabesh, and Askari-Nasab (2018, 2019) developed multiple objective truck dispatching models that can be implemented in mines where a heterogeneous truck fleet is used. Despite other available models, their developed models do not place limitations on the number of trucks to be assigned each time the decision-making model solves the problem. However, their developed models do not incorporate uncertainty.
All the dispatching models published to date are deterministic. These models do not account for the imprecision of the input parameters. However, almost all of the input parameters of a truck dispatching model are estimated values of future actions. For example, the travel of a truck from its current location to a shovel is a process that will happen after solving the dispatching problem for that particular truck. Thus, at the time of solving the problem, the models use either the expected or estimated value for the truck's travel time. This assumption pushes truck dispatching models to make decisions that are far from reality.
One way of dealing with the problems where some of the input parameters are from future events is to use the concept of fuzzy set theory. The fuzzy set theory was first applied in the field of mining engineering in the late 1980s by Nguyen (1985), Bandopadhyay and Chattopadhyay (1986), and Bandopadhyay (1987). Since then, it has been extensively applied in decisionmaking models for mine planning (Rahmanpour and Osanloo, 2017), equipment selection and sizing (Bascetin, Oztas, and Kanli, 2007; Aghajani Bazzazi, Osanloo, and Soltanmohammadi, 2008), plant location selection (Yavuz, 2008), and post-mining land use and reclamation (Bangian et al., 2012). The application of fuzzy set theory in conventional linear programming resulted in the generation of fuzzy linear programming (FLP). The first implementations of FLP are credited to Zimmermann (1976, 1978) and Madadi and Wong (2014), and the latest application in the mining context can be found in Rahmanpour and Osanloo (2017). In this paper, we apply the concept of fuzzy set theory, using FLP, to solve our developed model for the truck dispatching problem in surface mines.
Model formulation
We first developed a deterministic mixed integer linear programming (MILP) model to solve the truck dispatching problem. The developed deterministic MILP model deals with the first limitation mentioned in the introduction by including the goals of the truck fleet, the shovel fleet, and the processing plants in the objective function. The model also removes the second limitation of the available truck dispatching models by adding an objective to meet the production target for each path. We explicitly introduce the deterministic model in this section.
The following parameters and variables were used in the development of the deterministic MILP model.
ltttdLoaded travel time from current truck t position to dump d, which is calculated as ldtd/lvtwhere, ldtdis the distance from current truck t position to dump d, and lvtis the loaded velocity of truck
qttdThe time truck t must spend in the queue at dump d waiting for permission to dump its material
dttdThe time truck t spends at dump d to back up and dump its load into the dumping area
etttsTime it takes truck t to travel empty from where its empty travel starts to shovel s, which is calculated as edts/evt where edtsis the distance from current truck t position to shovel s, and evtis the empty velocity of truck t.
tinqttsTime a truck of type tt that is already in the queue must spend in shovel s queue
tenrttsTime a truck of type tt must travel from its current position to reach shovel s before truck t
stttsSpot time for a truck of type tt at shovel s
ltttsLoading time for a truck of type tt at shovel s
tctCapacity of truck t (tons)
TCtNominal truck capacity for truck t (tons)
scsCapacity of shovel s
pcdCapacity of dump d (tons per hour)
mfThe factor that shows what portion of the current
demands can be met with the available trucks pfsdOptimal flow rate for the path from shovel s to dump d
based on upper stage decisions pmsfsdPortion of the required path flow rate for the current
period that has been met so far
Variables:
xtdsBinary integer variable to assign truck t to the path connecting shovel s to dump d AF Variable factor that adjusts trucks available to be assigned with the demands of dumping locations.
The deterministic MILP model is presented in Equations [1] to [8]. The objective function of the model consists of two parts. The objective coefficient of the first part is calculated using Equation. [1]:
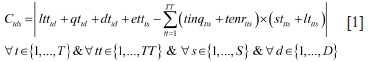
where Ctdsis the time difference between the time truck t will reach to shovel s after dumping its load at dump d and the next time shovel s will be available.
In the first part of the objective function, the MILP model minimizes the summation of Ctds(Equation [1]) over all the possible truck dispatching decisions.
In the second part of the objective function, our developed MILP model optimizes the production target of the available paths. The MILP model minimizes the deviation from the production target of the paths by maximizing the adjustment factor (AF). To eliminate the effect of the second part of the objective function on the decisions of the first part, we multiply it with a very big number (VBN). The AF appears two more times in the model. The first time it is presented is in Equation [5], where it adjusts the inequality constraint for delivering enough material to the processing plants. The second appearance of the AF in the model is in Equation [6]. In Equation [6], AF is limited to values less than or equal to unity or the match factor (mf). The definition of mf is essential for the model. As presented in Equation. [8], mf is defined as the cumulative capacity of the trucks requesting the next destination, at the time of running the mathematical model, divided by the cumulative production target of the active paths.
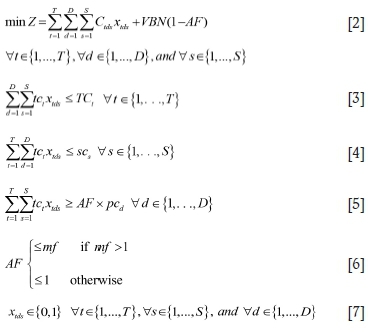

The decisions are made by optimizing the objective function under the operational constraints [3] to [8]. Constraint [3] makes sure that the truck t cannot accept loads greater than its nominal capacity. Constraint [4] ensures that the summation of truck capacities assigned to a shovel does not exceed the nominal digging rate of that particular shovel. Constraint [5] limits the model to sending at least AF times the plant capacity to each plant. Constraint [6] puts an upper limit cap on AF. Finally, Equation [7] guarantees that the decision variables can take only binary integer values.
After developing the deterministic model, we identified the fuzzy parameters involved in the proposed model. Then, based on the identified fuzzy parameters, we translated the deterministic MILP model to an FLP model. The fuzzy version of our deterministic MILP model can be presented as follows.

It is worth noting that X represents the fuzzy version of parameter x in the deterministic MILP model.
Defuzzification of the model
The uncertainties in the input parameters of the FLP model cause two significant problems: the problem of extracting optimum objective function value-containing fuzzy parameters, and the problem of the relationship between fuzzy sides of the constraints. Solving these two problems is tied to the process of ranking fuzzy numbers (Madadi and Wong, 2014). Several approaches have been introduced in the literature for the application of fuzzy set theory to rank fuzzy numbers. A detailed explanation of these approaches can be found in Lai and Hwang (1992) and van Leekwijck and Kerre (1999).
In this research, we implement the method developed by Jiménez et al. (2007) to rank the fuzzy constraints and fuzzy objective functions. The technique uses the concept of optimality to deal with the fuzzy objective functions and the idea of feasibility to deal with the fuzzy constraints. One essential advantage of ranking fuzzy numbers by implementing this method is that it preserves the linearity of the LP model, which helps to present a computationally efficient model to solve. The technique developed by Jiménez et al. (2007) is also capable of preventing the number of constraints or objective functions from increasing (Ghasemy Yaghin, Torabi, and Fatemi Ghomi, 2012). Thus, it can be implemented for solving large-scale FLP models (Madadi and Wong, 2014).
The method developed by Jiménez et al. (2007) is based on two mathematically strong concepts of expected value and expected interval of fuzzy numbers (Pishvaee and Torabi, 2010) that were initially presented by Yager (1981) and Dubois and Prade (1987) and was developed later by Heilpern (1992) and Jiménez et al. (2007).
To start with the denazification process, we first define some essential terms. A fuzzy number is defined as a fuzzy set on the real line R that has a membership function presented in Equation [14].

A cut through the fuzzy number produces a non-fuzzy set and is defined as given in Equation [15].

The membership function for cases where faand gaare linear functions is trapezoidal, and in cases where a2 = a3 and the fa and gaare linear functions, triangular. In this paper, all the parameters are assumed to follow the triangular membership function. The expected interval and the expected value of a triangular fuzzy number, which were first introduced by Heilpern (1992), can be calculated using Equation [16] and Equation [17], respectively.
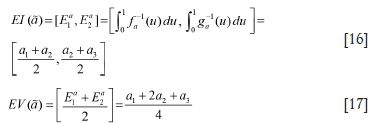
According to the ranking method developed by Jiménez et al. (2007), a is greater than or equal to b in the degree defined by Equation [18] (Pishvaee and Torabi, 2010).

If μm (ã,b) > a then it is said that at least in the degree of a, ã is greater than or equal to b. Based on Arenas Parra et al. (2005), ã and b are equal in degree of a if:

The FLP models with trapezoidal or triangular fuzzy parameters (Equation [20]) can be converted to their equivalent crisp models (Equation [21]) by implementing the definitions explained above and the Jiménez et al. (2007) method for treating fuzzy objective function and the Arenas Parra et al. (2005) method for treating fuzzy constraints.

min EVy(Z) = EVy (a) x

With y degree of optimism, the objective function (EVy(Z) = EVy (a) x) where Z = Z1, Z2, Z3, Z4), can be defined as:
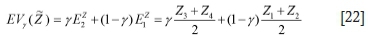
Using the defuzzification method explained in Equations [14] to [22], the equivalent crisp model for the fuzzy truck dispatching model presented in this paper can be formulated as follows:

Subject to
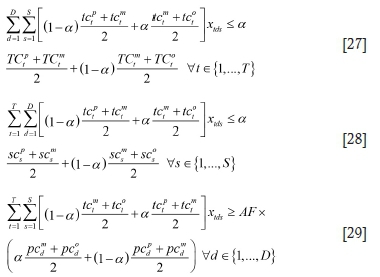

where y is the degree of optimism of the decision-maker and a is the degree of the minimum acceptable feasibility of the decision vector (Madadi and Wong, 2014).
Application in a case study
We applied the FLP model in a mining case study to evaluate its performance. The case study is an opencast iron ore mine located in central Iran. The mine has two processing plants fed by a truck and shovel material handling system. Based on the short-term production schedule of the mine, the production fleet must be capable of meeting an hourly feed rate of 2300 t for each of the active processing plants with a stripping ratio of 1.3.
The material handling fleet consists of two types of shovels (Hitachi Hit 2500 and Hit 5500), and one type of truck (Cat 785C). The mine has five active faces. Two small shovels (Hit 2500) work on the ore mining faces and serve the processing plants. Two large shovels (Hit 5500) and one small shovel work on the waste mining faces. The mined material is transported to the destination areas (plants or waste dumps) using 28 trucks. The operation uses an optimization model developed by White and Olson ( 1986) and Olson, Vohnout, and White (1993) to solve its truck dispatching problem. We used that model as the benchmark in this study.
Input from historical data
We incorporated uncertainties associated with all the parameters in the simulation model of the case study and the truck dispatching model. To do so, we first retrieved one year of operational data from the fleet database. Then, after preprocessing and cleaning bad data, we fitted several distributions to the data. We then selected the best-fitted distribution on each parameter using the results of the chi-square test and Kolmogorov-Smirnov test (Rossetti, 2015). The parameters and the best distributions fitted on them are presented in Table I.
In Table I, bcsis shovel s bucket capacity, and lctsis the loading cycle time for shovel . The distributions provided in Table I are used in the simulation model of the case study. Whenever a value for a parameter is required, the random sampler of the simulation software, Rockwell Arena (Rockwell Automation Technologies Inc., 2020) in our case, randomly samples from the parameter's associated distribution to incorporate uncertainty into the simulation modelling. Any time a signal is received by the truck dispatching model, a triangular function with a minimum of the first quantile, mean of the second quantile, and maximum of the third quantile is exported from the parameters presented in Table I to be used in the FLP model. For the parameters such as the nominal capacity of trucks, hourly capacity of shovels, and hourly capacity of plants, a ±10% value from the manufacturer's catalogues was selected to be used as the minimum and maximum values in the triangular fuzzy function of the parameters. For instance, for the Cat 785C, with a nominal capacity of 140 t, the triangular function has a minimum of 126 t and a maximum of 154 t. The ±10% of nominal capacity is sourced from the manufacturer's catalogues as the capacity to be used for the best practice and the lowest operational and maintenance costs. Each time the FLP model is called for making a decision, it uses y (the degree of optimism of the decisionmaker) and a (the degree of the minimum acceptable feasibility of the decision vector) to sample from the triangular distributions of the fuzzy parameters and apply those parameters in its calculations.
The model set-up and evaluation
Material handling in surface mines is an expensive operation. Because of that, testing of developed technologies in a real mining operation is not economically viable. Therefore, researchers test new technologies on the simulated version of a mining operation before implementing them in the actual operations. We followed the same route in this paper. We used the simulation model of the case study developed by Moradi Afrapoli et al. (2018) to evaluate the performance of the FLP truck dispatching model. The simulation of the case study was run for ten days of operation, each day consisting of one 12-hour shift. We used the first shift of the simulated operation to warm up the simulation model and to reach steady-state operation. Then, we evaluated the performance of our developed model by comparing the results of its application in the next nine shifts with the results from the mine's in-place truck dispatching model.
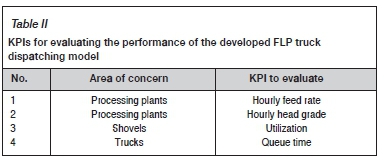
Based on the short-term schedule, in 120 hours of operation, 1.2696 Mt of ore plus waste should be removed from the pit. The simulation of the operation meets the criteria with its in-place truck dispatching model and our FLP truck dispatching model. Apart from the total material removed, other key performance indicators (KPIs) were measured in the case study. Table II lists the measured KPIs.
As the processing plant is one of the most expensive parts of a mining operation, keeping its performance at the highest level is essential. One responsibility of the material handling system is to feed the processing plant to its full capacity. The case study involves two processing plants. The truck and shovel fleet of the operation works towards delivering 27.60 kt of ore to each plant per shift to meet the full capacity requirement. In other words, the material handling system delivers 2300 t of ore to each processing plant in each hour of the operation. Figure 1 shows how each processing plant was fed during the simulation.
Implementation of our developed model instead of the inplace model improved the hourly ore delivery to plant 1 (Figure 1a and plant 2 (Figure 1b) by 21% and 15%, respectively. The leading cause of this improvement is the incorporation of AF as the second component of our objective function (Equation [2]). This component of the objective function minimizes the deviation from the plant capacity. In addition to the tonnage of material delivered to the processing plants, another essential factor to be met is the quality (grade) of the material. The processing plants accept ore with magnetic weight recovery (MWT) grade of between 60% and 80%. Preference for plant 1 is an average MWT grade of 65%, and for plant 2 an average of 75%. Figure 2 represents the distribution of MWT grade in material delivered to each plant on a shift-by-shift basis.
As depicted by Figure 2, both of the truck dispatching models delivered material to the plants within the acceptable MWT grade range. However, by replacing the in-place truck dispatching model with the FLP model, the tendency of the MWT grade towards the desired average MWT grade (65% for plant 1 and 75% for plant 2) increased.
In the case study, five shovels are working in the fleet to fulfill the short-term production schedule requirement. Shovel 1 and shovel 2 are at the ore mining faces, and the remainder of the shovels at the waste mining faces. Table III represents utilization for each active shovel and the entire shovel fleet in the simulation study of the mine.
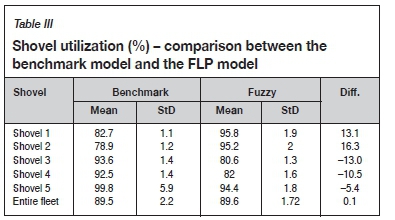
Table III shows that although both truck dispatching models utilized the shovel fleet almost the same, the benchmark model used the waste shovels more than the ore shovels. The benchmark truck dispatching model sends trucks to the closest shovels without prioritizing any particular shovel. In the case study, waste shovels are mining overburden and sitting closer to dumping location than the ore shovels. Thus waste shovels are utilized more than ore shovels. However, according to the same table, the FLP truck dispatching model employed the ore shovels more than the waste shovels. Instead of the unnecessary waste movement required by the production schedule, the FLP model prioritized the ore shovels to meet the requirement of the processing plants.
A fleet of 28 Cat 785C trucks transports material from the mining faces to the destinations (either crushers or waste disposal area). The cumulative time that each truck spent in the queue is presented in Figure 3. The fleet in the benchmark truck dispatching model wasted an average of 1486±71 minutes per truck in the queue during the simulation. Replacing the benchmark dispatching model with the FLP truck dispatching model improved truck fleet efficiency. The FLP model utilized the truck fleet such that each truck spent a cumulative average of 1253±50 minutes in different queues (a 15% improvement) during the simulation.
This time saving is due to the incorporation of the length of the queue in the decision-making procedure. The in-place truck dispatching model (and most of the published truck dispatching models) ignores the expected queue time for the trucks. However, our developed model incorporates the expected queue time, which helps in making more precise decisions with less wait time in queues for trucks.
Conclusions
This paper introduced a new mixed-integer linear programming model to solve the truck dispatching problem in surface mines. The proposed model makes dispatching decisions by simultaneously minimizing deviation from the production target set by the strategic plan, cumulative idle time of the shovel fleet, and cumulative wait time of the truck fleet. The model applies a fuzzy linear programming approach to incorporate the associated uncertainties in the decision-making procedure. We used the developed truck dispatching model in a real mining case study with a benchmark from the backbone algorithm of Modular Mining DISPATCH® (Modular Mining Systems Inc., 2020). The results showed that our FLP model improved the ore production and truck wait time in the queues by more than 15%. The model also prioritized ore shovels over waste shovels in order to feed the plants to their maximum capacity. This improvement in production and equipment efficiency will result in lower costs and higher profits for the operation. The authors anticipate that implementing the developed FLP model in a case with a fleet of mixed truck types will result in more realistic truck dispatching decisions.
References
Aghajani Bazzazi, A., Osanloo, M., and Soltanmohammadi, H. 2008. Loading-haulage equipment selection in open pit mines based on ftizzy-TOPSIS method. Gospodarka Surowcami Mineralnymi Mineral Resources Management. Journal of the Polish Academy of Sciences, vol. 24, no. 4, part 3. pp. 87-102. [ Links ]
Akbari, A.D., Osanloo, M., and Shirazi, M.A. 2009. Minable reserve estimation while determining ultimate pit limits (UPL) under price uncertainty by real option approach (ROA). Archives of Mining Sciences, vol. 54, no. 2. pp. 321-339. [ Links ]
Alarie, S. and Gamache, M. 2002. Overview of solution strategies used in truck dispatching systems for open pit mines. International Journal of Surface Mining, Reclamation and Environment, vol. 16, no. 1. pp. 59-76. doi: 10.1076/ijsm.16.1.59.3408 [ Links ]
Arenas Parra, M., Bilbao Terol, A., Pérez Gladish, B., and Rodriguez Uria, M.V. 2005. Solving a multiobjective possibilistic problem through compromise programming. European Journal of Operational Research, vol. 164, no. 3 (Special Issue), pp. 748-759. doi: 10.1016/j.ejor.2003.11.028 [ Links ]
Bandopadhyay, S. 1987. Partial ranking of primary stripping equipment in surface mine planning. International Journal of Surface Mining, Reclamation and Environment, vol. 1, no. 1. pp. 55-59. doi: 10.1080/09208118708944102 [ Links ]
Bandopadhyay, S. and Chattopadhyay, A. 1986 Selection of post-mining uses of land via fuzzy algorithm. Proceedings of the 19th International Symposium on the Application of Computers in Mine Planning. Ramani, R.V (ed.). Society of Mining Engineers of AIME. pp. 321-332. [ Links ]
Bangian, A. H., Ataei, M., Sayadi, A., and Gholinejad, A. 2012. Optimizing post-mining land use for pit area in open-pit mining using fuzzy decision making method. International Journal of Environmental Science and Technology, vol. 9, no. 4. pp. 613-628. doi: 10.1007/s13762-012-0047-5 [ Links ]
Bascetin, a., Oztas, o., and Kanli, A. 2007. A computer software using fuzzy logic for equipment selection in mining engineering. Journal of the Southern African Institute of Mining and Metallurgy, vol. 106, no. 1. pp. 63-70. https://journals.co.za/content/saimm/107/2/AJA0038223X_3299 [accessed: 1 March 2018]. [ Links ]
Dubois, D. and Prade, H. 1987. The mean value of a fuzzy number. Fuzzy Sets and Systems, vol. 24, no. 3. pp. 279-300. doi: 10.1016/0165-0114(87)90028-5 [ Links ]
Ghasemy Yaghin, R., Torabi, S.A.A., and Fatemi Ghomi, S.M.T.M.T. 2012. Integrated markdown pricing and aggregate production planning in a two echelon supply chain: A hybrid fuzzy multiple objective approach. Applied Mathematical Modelling, vol. 36, no. 12. pp. 6011-6030. doi: 10.1016/j.apm.2012.01.029 [ Links ]
Hauck, R.F. 1973. A real-time dispatching algorithm for maximizing open-pit mine production under processing and blending requirements. Proceedings of the Seminar on Scheduling in Mining, Smelting and Metallurgy: Canadian Institute of Mining, Metallurgy and Petroleum, Montreal. pp. 1-10. [ Links ]
Heilpern, S. 1992. The expected value of a fuzzy number. Fuzzy Sets and Systems vol. 47, no. 1. pp. 81-86. doi: 10.1016/0165-0114(92)90062-9 [ Links ]
Jiménez, M., Parra, M.A., Bilbao-Terol, A., and Rodríguez, M.v. 2007. Linear programming with fuzzy parameters: An interactive method resolution. European Journal of Operational Research, vol. 177, no. 3. pp. 1599-1609. doi: 10.1016/j.ejor.2005.10.002 [ Links ]
Lai, Y.-J and Hwang, C-L. 1992. A new approach to some possibilistic linear programming problems. Fuzzy Sets and Systems, vol. 49, no. 2. pp. 121-33. doi: 10.1016/0165-0114(92)90318-X [ Links ]
Li, Z. 1990. A methodology for the optimum control of shovel and truck operations in open-pit mining. Mining Science and Technology, vol. 10, no. 3. pp. 337-340. doi: 10.1016/0167-9031(90)90543-2 [ Links ]
Madadi, N. and Wong, K.Y. 2014 A multiobjective fuzzy aggregate production planning model considering real capacity and quality of products. Mathematical Problems in Engineering, 2014. doi: 10.1155/2014/313829 [ Links ]
Modular Mining Systems Inc. 2020. Dispatch. http://wwww.modularmining.com/product/dispatch/ [ Links ]
Moradi Afrapoli, A. and Askari-Nasab, H. 2019. Mining fleet management systems: a review of models and algorithms. International Journal of Mining, Reclamation and Environment, vol. 33, no. 1. pp. 42-60. doi: 10.1080/17480930.2017.1336607 [ Links ]
Moradi Afrapoli, A., Tabesh, M., and Askari-Nasab, H. 2018. A stochastic hybrid simulation-optimization approach towards haul fleet sizing in surface mines. Mining Technology: Transactions of the Institute of Mining and Metallurgy. doi: 10.1080/25726668.2018.1473314 [ Links ]
Moradi Afrapoli, A., Tabesh, M., and Askari-Nasab, H. 2019. A multiple objective transportation problem approach to dynamic truck dispatching in surface mines. European Journal of Operational Research, vol. 276, no. 1. pp. 331-342. doi: 10.1016/j.ejor.2019.01.008 [ Links ]
Nguyen, V.U. 1985. Some fuzzy set applications in mining geomechanics. International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts, vol. 22, no. 6. pp. 369-379. doi: 10.1016/0148-9062(85)90002-6 [ Links ]
Olson, J.P., Vohnout, S.I., and White, J. 1993. On improving truck/shovel productivity in open pit mines. CIM Bulletin, vol. 86, no. 973. pp. 43-49. [ Links ]
Oraee, K. and Goodarzi, A. 2007. General approach to distribute waste rocks between dump sides in open cast mines. Proceedings of the Sixteenth International Symposium on Mine Planning and Equipment Selection. Bangkok, Thailand. Reading Matrix Inc., Irvine, CA. pp. 701-712. [ Links ]
Pishvaee, M.S. and Torabi, S.a. 2010. A possibilistic programming approach for closed-loop supply chain network design under uncertainty. Fuzzy Sets and Systems, vol. 161, no. 20. pp. 2668-2683. doi: 10.1016/j.fss.2010.04.010 [ Links ]
Rahmanpour, M. and Osanloo, M. 2017. Application of fuzzy linear programming for short-term planning and quality control in mine complexes. Journal of the Southern African Institute of Mining and Metallurgy, vol. 117, no. 7. pp. 685-694. [ Links ]
Rockwell Automation Technologies Inc. 2020. Arena Simulation Software. Austin, TX. https://www.arenasimulation.com [ Links ]
Rossetti, M.D. 2015. Simulation Modeling and Arena. 2nd edn. Wiley, Hoboken, NJ. https://books.google.com.tr/books?id=j2xuCAAAQBAJ [ Links ]
Soumis, F., Ethier, J., and Elbrond, J. 1989. Truck dispatching in an open pit mine. International Journal of Surface Mining, Reclamation and Environment, vol. 3, no. 2. pp. 115-119. doi: 10.1080/09208118908944263 [ Links ]
Temeng, V. a., Otuonye, F.O., and Frendewey, J.O. 1997. Real-time truck dispatching using a transportation algorithm. International Journal of Surface Mining, Reclamation and Environment, vol. 11, no. 4. pp. 203-207. doi: 10.1080/09208119708944093 [ Links ]
Temeng, V.A., Otuonye, F.O., and Frendewey, J.O. 1998. A non preemptive goal programming approach to truck dispatching in open pit mines. Mineral Resources Engineering, vol. 7, no. 2. pp. 59-67. doi: doi:10.1142/S0950609898000092 [ Links ]
Upadhyay, S.P.P. and Askari-Nasab, H. 2016. Truck-shovel allocation optimisation: A goal programming approach. Mining Technology, vol. 125, no. 2. pp. 1-11. doi: http://doi.org/10.1179/1743286315Y.0000000024 [ Links ]
White, J.W. and Olson, J.P. 1986. Computer-based dispatching in mines with concurrent operating objectives. Mining Engineering, vol. 38, no. 11. pp. 1045-1054. [ Links ]
Van Leekwijck, W. and Kerre, E.E. 1999. Denazification: criteria and classification. Fuzzy Sets and Systems, vol. 108, no. 2. pp. 159-178. doi: 10.1016/S0165-0114(97)00337-0 [ Links ]
Yager, R.R. 1981. A procedure for ordering fuzzy subsets of the unit interval, Information Sciences, vol. 24, no. 2. pp. 143-161. doi: 10.1016/0020-0255(81)90017-7 [ Links ]
Yavuz, M. 2008. Selection of plant location in the natural stone industry using the fuzzy multiple attribute decision making method. Journal of the Southern African Institute of Mining and Metallurgy, vol. 108, no. 10. pp. 641-649. http://www.scielo.org.za/scielo.php?script=sci_arttext&pid=S2225-62532008000900008 [accessed: 1 March 2018]. [ Links ]
Zimmermann, H.-J. 1978. Fuzzy programming and linear programming with several objective functions, Fuzzy Sets and Systems, vol. 1, no. 1. pp. 45-55. doi: 10.1016/0165-0114(78)90031-3 [ Links ]
Zimmermann, H. 1976. Description and optimization of fuzzy systems. International Journal of General Systems, vol. 2, no. 4. pp. 209-215. doi: 10.1080/03081077608547470 [ Links ]
 Correspondence:
Correspondence:
A. Moradi-Afrapoli
Email: moradiaf@ualberta.ca
Received: 6 Dec2018
Revised: 29 May 2020
Accepted:28 Jul. 2021
Published: September 2021













