RESEARCH ARTICLE

 

Bridging gaps: Enhancing holistic support in mathematics during the transition from secondary school to university

 

Ukunqotshwa kwezinkinga: Ukuqinisa ukusekelwa okuphelele ngokufundiswa ngesifundo sezibalo kusukela emazingeni aphansi kuya emazingeni emfundo ephakeme inyuvesi

 

 

Alfred Mvunyelwa Msomi^I; Ekaterina Rzyankina^II

^IHead of Department: Mathematical Sciences (substantive); Acting Dean: Department of Mathematical Sciences, Faculty of Applied and Health Sciences, Mangosuthu University of Technology, Umlazi, South Africa. Email: alfred@mut.ac.za. ORCID: 0000-0002-2852-431
^IILecturer; Research Associate: Department of Maritime Studies, Faculty of Engineering and the Built Environment, Granger Bay Campus, Cape Peninsula University of Technology, Cape Town, South Africa. Email: rzyankinae@cput.ac.za. ORCID: 0000-0003-1532-6559

 

 

---

ABSTRACT

The provision of multidimensional holistic support in mathematics for students transitioning from secondary school to university is identified as a challenge facing global education systems, including in South Africa. Ongoing attempts to select effective mathematics learning support reflect the enduring nature of a problem caused by a range of factors. Despite a wealth of literature on the topic there has been little effort to consolidate the diverse knowledge on this issue into a comprehensive, useful understanding. This study aims to close this gap by synthesising and integrating the disparate elements with the aim of producing a unified framework to address the problem. The research employs a comprehensive rapid literature review following PRISMA (preferred reporting items for systematic reviews and meta-analyses) guidelines. The review concentrates on papers that investigate the impact of specific types of mathematical support; on those conducting analyses of the efficacy of distinct mathematical support approaches; and on those proposing solutions towards improving first-year South African university students' mathematical performance. To mitigate bias, the Rayyan Al-assisted literature review platform is utilised with the aim of promoting a rigorous, unbiased selection process. This rapid literature review reveals the absence of a unified framework for providing holistic mathematics learning support, which is a major obstacle to the provision of such support. The authors note that this deficiency can detrimentally impact students, underscoring the need for a comprehensive approach. The findings suggest that mathematics support can be enhanced by integrating the core elements of a holistic approach and acknowledging the interconnectedness and mutual influence of the various elements.

Keywords: Holistic approach, mathematics support, first-year engineering students, transition from secondary school to university, engineering education

---

ISIFINYEZO

Ukuhlinzekwa ngosizo olunobubanzi obuhlangene noluhlanganisa zonke izinsiza kufunda ekufundeni isifundo sezibalo kubafundi abaphumelele umatikuletsheni kuya ezingeni laseyunivesithi kuwumqansa ohlangabezwa izinhlelo zemfundo emhlabeni jikelele, kuhlanganisa naseNingizimu Afrika. Imizamo eqhubekayo yokukhetha izindlela eziphumelelayo zokwesekwa ekufundeni izibalo ibonisa isimo esinzima esibangelwa izinkinga eziningi ezihlangene. Naphezu kobuningi bemibhalo yesayensi, kuye kwaba nomzamo omncane wokuhlanganisa le mithombo ehlukene ukuze kutholakale ukuqonda okuhle nokuwusizo. Lolu cwaningo luqonde ukuvala leli gebe ngokuhlanganisa amasu ahlukene abe uhlaka oluhlangene. Ucwaningo lusebenzisa ukubuyekezwa kwemibhalo okujulile futhi okusheshayo, kuhanjiswa ngokuqapha iznkombandlela ze-PRISMA. Lolu cwaningo lugxile emaphepheni ahlola umthelela wezinhlobo ezithile ezilandelwayo ekufindeni izibalo, kulabo abenza izibuyekezo zokusebenza kahle kwezindlela ezihlukile zosizo lwezibalo, kanye namaphepha aphakamisa izixazululo zokuthuthukisa ukusebenza kwabafundi baseNingizimu Afrika abenza unyaka wokuqala ezifundweni zezibalo. Ukuze kugwenywe ukuchema, kusetshenziswe ipulatifomu ye-Rayyan esekelwa yi-AI yokubuyekezwa kwemibhalo, ukuqinisekisa inqubo eqinile nengachemile yokukhetha. Lolu cwaningo lwembula isithiyo esijwayelekile sokwesekwa ekufundeni izibalo ngokubanzi, ngendlela yokungabi khona kohlaka oluhlangene. Sibonisa ukuthi lokhu kushoda kungaba nomthelela ongemuhle kubafundi, kuphinde kugcizelele isidingo sokusebenzisa indlela ebanzi. Imiphumela iphakamisa ukuthi ukwesekwa kwezibalo kungathuthukiswa ngokuhlanganisa izici eziyinhloko zendlela ehlangene, kanye nokwamukela ukuxhumana kanye nomthelela omkhulu wezinto ezahlukene ezihlangene.

Amagama Angukhiye: Indlela ehlangene, ukwesekwa kwezibalo, abafundi be-injiniyeringi bonyaka wokuqala, ukudlulela eyunivesithi usuka emfundweni yesiseko

---

 

 

Introduction

Transitioning from high school to university presents significant challenges for South African students, especially around mathematics (Selesho, 2012; Kizito et al., 2016) and particularly for those students from previously 'disadvantaged', under-resourced schools. The shift, particularly in subjects like calculus, represents a critical hurdle for many students and can affect their retention in technical programmes (Yoon et al., 2018). Early strong mathematics performance is crucial for academic success in STEM subjects (Sithole et al., 2017). Despite efforts to remedy the situation, student performance in mathematics has remained relatively unchanged over time, highlighting persistent challenges (Faulkner et al., 2010; Kizito et al., 2016). The problem of performance stems from such factors as students' negative attitudes towards mathematics; their levels of competence; and the socio-economic context (Rach & Heinze, 2017). Addressing these challenges requires a holistic approach, one that includes academic, psychosocial and foundational dimensions (Ward et al., 2014).

A holistic approach in this context refers to a comprehensive perspective on student mathematical development, one that recognises the interrelated elements of curriculum design; instructional practices; assessment strategies; and socio-emotional factors. Such an approach would integrate these components to create a cohesive system that promotes understanding and success among students.

Disconnected and fragmentary programmes have not been found to improve retention, success or graduation rates in mathematics (Palmer, 2016; Tierney & Sablan, 2014), indicating the importance of designing more integrated support initiatives to obviate the confusion arising from uncoordinated interventions (Palmer, 2016). A significant research gap exists in exploring holistic perspectives to enhance first-year mathematics students' understanding and motivation (Venezia & Jaeger, 2013). Accordingly, the authors of this article argue for addressing this gap by establishing a unified framework to improve conceptual understanding and graduation rates.

This review seeks to provide insights into the current landscape of mathematical support for first-year university students in South Africa (SA) and proposes specific strategies to enhance their learning experiences. It explores the development of a framework to improve fragmented support and argues for the potential benefits of a holistic perspective in enhancing mathematical proficiency. It further references the importance of developing mathematical skills for the success of students in STEM degree programmes (Deeken et al., 2020).

The review poses three research questions:

1. What are the prevalent challenges and gaps in mathematics support encountered by students transitioning from secondary schools to universities?

2. What existing strategies, interventions and programmes have been proposed or implemented to address fragmented mathematics support during the transition period, and what evidence exists regarding their effectiveness?

3. How can a comprehensive synthesis of literature on mathematics support assist in developing a unified framework that effectively addresses the diverse needs and education backgrounds of students engaging in mathematics as they transition from secondary school to university?

The study is organized as follows: first, it examines the current body of knowledge on mathematics support programmes for first-year university students; then it discusses the research methodology used in the review. The findings section introduces a holistic approach to mathematics support and presents a visual framework for students to help them develop and apply certain concepts/connections and enhance their understanding. The article concludes with a discussion of the possibilities for new research in this area.

 

Literature review

This literature review seeks to explore critical aspects surrounding mathematical support for first-year university students, examining key issues, prevalent challenges and emerging initiatives. It addresses the issue of first-year university students' failure rates in mathematics. It explores the factors contributing to this, and the implications for educational practice. It examines evidence of the fragmentary nature of the mathematical support on offer to first-year students, identifying gaps and inefficiencies. It also considers the various integrated and holistic mathematics support initiatives on offer, synthesising research perspectives to understand and assess the potential benefits and challenges of adopting a holistic approach.

 

First-year university students' failure rates in mathematics

Adamuti-Trache et al. (2013) explored factors influencing successful transitions from high school to university in mathematics at the University of British Columbia. They examined performance gaps and school effectiveness, emphasising the crucial role of high-school programmes in shaping student preparedness. They concluded that a student's first-year university mathematics performance is closely tied to the high school they attended.

Another study investigated prerequisites for individual mathematical learning among 182 first-term university students majoring in mathematics (Rach & Heinze, 2017). The authors found that, while school-related mathematical resources had a minor impact, students' prior knowledge and the effectiveness of their learning strategies during the transition had a relatively great influence on their prospects of success.

Park et al. (2018) analysed the impact of optional developmental education on underprepared first-time university students in Florida in the United States (US). Their study revealed that many students chose not to enrol for optional courses, leading to lower success rates in mathematics at the post-secondary level. However, they found that underprepared students performed better in modified developmental courses compared with courses with developmental support.

Berry et al. (2015) conducted a study at Maynooth University in Ireland on student engagement with a mathematics support-centre website. They identified a lack of institutional information and training in relation to using technology, as well as a lack of suitable online resources to support student performance. Their recommendations included the establishment of a modern website design, and comprehensive training and support for students and lecturers. Kizito et al. (2016) also emphasise the importance of integrating technology into mathematics education to bridge resource gaps. Their study on mobile learning interventions in Uganda showed that tutorials and assessments significantly improved student engagement and performance in mathematics, offering a scalable solution to inadequate preparation among high-school graduates.

 

Holistic mathematics support in the African context

The educational landscape in Africa presents unique challenges and opportunities for holistic mathematics support. Selesho (2012) notes that the transition from high school to university in SA tends to be characterised by significant disparities in mathematical preparedness due to socio-economic factors and the varying quality of secondary education across the country. In this context, a holistic approach that addresses academic needs and considers the socio-emotional and foundational aspects of student development is required.

Mutodi and Ngirande (2014) explored the role of psychosocial support in enhancing mathematics performance among university students in SA. They found that students who received regular counselling and mentorship demonstrated marked improvements in mathematical understanding and overall academic performance. Highlighting the need for a support system that includes not only academic tutoring, but also psychological support and mentorship.

In a similar vein, Mayet (2021) examined the effectiveness of foundation programmes offered by South African universities to underprepared students transitioning to higher education. These programmes can include intensive mathematics courses; study skills workshops; and personal development sessions. The study concluded that such comprehensive support structures are crucial for improving retention and success rates in STEM disciplines.

 

Evidence of fragmented mathematical support

Koskinen and Pitkaniemi (2022) conducted a systematic study to address fragmentation in research on teaching and learning mathematics. Their goal was to create a comprehensive synthesis of the literature from diverse sources focusing on meaningful learning, or the lack thereof, in the education provided at schools. They examined correlations between various teaching approaches; interactions during the teaching-learning process; and learning outcomes. The study found that achieving high-quality learning outcomes in mathematics requires active guidance and immediate feedback during student activities. Additionally, an emotionally supportive classroom environment and the presence of teachers who consider students' unique needs and learning styles are required for a meaningful learning experience.

Research undertaken on technology-assisted mathematical support shows the potential of digital tools to enhance education. Bray and Tangney (2017) examined 139 recent studies on technological interventions in mathematics and developed a classification system to categorise digital tools; activity goals; pedagogical foundations; and levels of technological integration. Their analysis revealed a discrepancy between the focus of published research and the approaches to using technology that were most effective in enhancing mathematics teaching and learning.

 

Effectiveness of holistic framework components

Research has shown the effectiveness of including several components within a holistic mathematics support framework. De Jesus (2012) highlighted the importance of such tailored instructional practices as differentiated instruction and personalised learning plans. Those students who received customised learning experiences demonstrated significant improvements in their mathematical skills and overall academic performance.

Psychosocial support is another crucial component of a holistic framework. Arif and Mirza (2017) found that students who participated in programmes which included counselling, mentorship, and stress management workshops exhibited higher levels of academic resilience and motivation than those who did not. From such studies one can conclude that a supportive learning environment may be fostered by addressing students' emotional and psychological needs.

Studies conducted by Kizito et al. (2016) and Bray and Tagney (2017) show the importance of the role of technology in providing effective mathematics support. Shi et al. (2020) conducted a meta-analysis of online learning studies, concluding that students in technology-enhanced learning environments performed better than those in traditional settings. Such studies show the value of incorporating adequate digital tools and resources into mathematics support programmes to enhance learning outcomes.

Several studies have found collaborative learning to be effective within a holistic framework. Almajed et al. (2016) found that collaborative learning strategies, such as group problem-solving and peer tutoring, improved students' mathematical understanding and promoted positive interdependence and accountability among peers. Thus, effective social interactions can be seen as crucial for developing critical thinking and problem-solving skills.

In addition, assessment and feedback have been found to be vital in the learning and transitional process. Irons and Elkington (2021) emphasise the importance of formative assessment in providing ongoing developmental feedback, and in helping students identify strengths and areas for improvement. Their research showed that formative assessments, when integrated into the learning process, significantly enhance student achievement and motivation.

 

Theoretical framework

The holistic approach informing this study is underpinned by Bronfenbrenner's (1977) ecological systems theory, which emphasises the complex interplay between individuals and their environmental contexts. The theory provides a comprehensive framework for understanding how different layers of the educational environment, from immediate settings (such as classrooms) to broader influences (such as educational policies), affect student learning and development. The study advocates for a shift towards holistic educational practices that prioritise both academic achievement and overall well-being, preparing students for the complex global challenges ahead.

 

Methods

To investigate the ongoing poor performance of first-year university mathematics students transitioning from secondary school, with an emphasis on the South African experience, a rapid literature review was undertaken. This approach allowed for a focused examination of recent empirical studies (2010-2022) on the topic. It entailed five steps: (1) identifying review questions; (2) identifying relevant studies; (3) selecting studies from the many potentially relevant studies; (4) charting data; and (5) summarising results (Arksey & O'Malley, 2005). Guided by the PRISMA framework (Moher et al., 2009) to enhance transparency and replicability, the methodology sought to adopt a rigorous and structured approach, contributing to the credibility and reliability of the findings.

The application of the PRISMA methodology promoted the establishment of a transparent and replicable research process. This methodology provided a clear framework for each phase of the review, from the initial identification of studies to the final synthesis of findings. The use of PRISMA also supported the review's aim to be comprehensive, capturing a wide range of relevant studies and minimising the risk of bias (Moher et al., 2009).

The PRISMA-guided review has highlighted the interconnectedness of various elements within a holistic approach to mathematics learning support. By systematically identifying and synthesising relevant studies, the review has provided robust evidence to support the implementation of holistic educational practices. The findings have emphasised the need for a comprehensive approach that addresses the cognitive, emotional, and social dimensions of learning so that student outcomes may be improved.

 

Identification phase

The initial phase of the PRISMA process - identification - involved a comprehensive search to capture a broad range of relevant literature, the aim being to avoid selection bias (Moher et al., 2016). Researchers have noted that an effective search approach should balance specificity and sensitivity, thus ensuring the inclusion of relevant studies while minimising the inclusion of unrelated research (Brunton et al., 2017). Relevance is seen as crucial for validity, safeguarding against selection and publication bias (Booth et al., 2016).

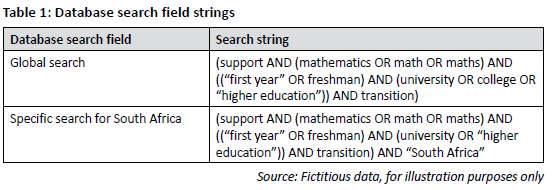
The search for this review spanned databases including Engineering Village, ERIC via EBSCOhost, and Scopus. The Rayyan Al-assisted platform was deployed to further fortify validity and avoid publication bias (Bartos et al., 2023). Search strings were developed with a university librarian, using Boolean operators 'OR' and 'AND', and proximity and truncation operators to balance sensitivity and specificity (see Table 1). The search strategy varied based on each database's characteristics.

 

 

The study selection process complied with the four PRISMA steps recommended by Moher et al. (2009), encompassing identification; screening; eligibility; and inclusion. Screening involved the independent assessment of abstracts and titles (n = 162), and articles in full text (n = 162). Ultimately, 30 studies met the inclusion criteria, as illustrated in Figure 1.

 

 

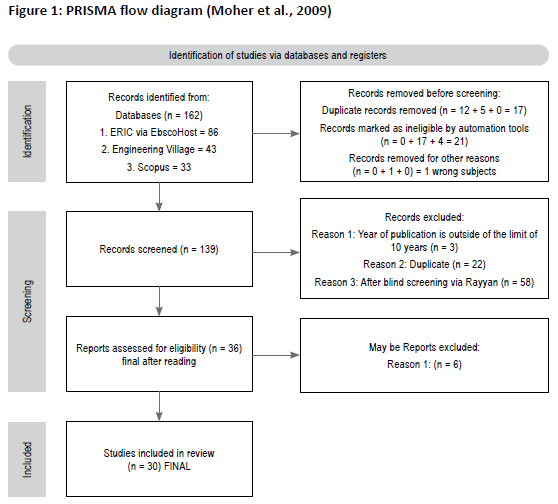
Screening phase

During the screening phase, the identified records were selected according to predefined inclusion and exclusion criteria. The inclusion criteria were established to ensure that the studies selected were relevant to the research questions, specifically focusing on holistic support in mathematics for first-year university students in SA. Exclusion criteria helped to eliminate studies that did not meet the relevance, quality or focus required for this review. This phase involved removing duplicates; reviewing titles and abstracts; and conducting a preliminary assessment of the full texts (Page et al., 2021).

 

Eligibility and inclusion phases

The eligibility phase involved a detailed examination of the full-text articles to confirm their suitability for inclusion in the review. Studies were assessed for their methodological quality; relevance to the research questions; and adherence to the defined inclusion criteria. This rigorous assessment ensured that only high-quality studies with significant contributions to the topic were included in the final review. To ensure the inclusion of recent research, only texts produced from 2010 to 2020 were considered, with language restrictions based on the reviewers' proficiency in English.

 

Data extraction and synthesis

The final set of included studies underwent a comprehensive data-extraction process. Key information, such as study objectives, methods, sample characteristics, findings, and implications, were systematically extracted and tabulated. The PRISMA framework facilitated the synthesis of these data, allowing for the identification of common themes, patterns, and gaps in the existing literature. This structured approach supported the production of a comprehensive, coherent synthesis and the provision of a clear understanding of the current state of research on holistic support in mathematics education (Page et al., 2021).

 

Ethical considerations

All extracted articles and resources were treated with respect for intellectual property rights. Citations were carefully recorded, and original authors were credited for their contributions.

 

Results

Research question 1

Examining the literature, several themes and findings were identified in response to the first research question posed by this study: What are the prevalent challenges and gaps in mathematics support encountered by students transitioning from secondary schools to universities?

Change in learning environment

There is a significant difference between the structured, teacher-led environment of secondary school to the more self-directed and independent learning style adopted at university; and this shift can have a significant impact on first-year students' understanding of mathematics at the university level. In the absence of the structure and guidance of a teacher-led environment, students can struggle to manage their time effectively; set meaningful study goals; engage deeply with the material; seek help when needed; receive feedback on their progress; and, ultimately, develop a comprehensive understanding of the subject. Smith and Thomas (2020) note that students face considerable difficulty in adjusting to the less structured, more autonomous nature of university learning environments.

Lack of prerequisite knowledge

A growing body of literature has investigated the lack of prerequisite knowledge on the part of first-year students as they transition from school-level to university-level mathematics (Hochmuth et al., 2021). Research has indicated that some first-year university students commence their academic journeys without a comprehensive grasp of essential mathematical concepts that should have been taught in secondary school, thus creating gaps in their understanding. This limitation impacts their comprehension of advanced mathematical topics and impedes their ability to follow lectures, execute assignments, and achieve satisfactory outcomes in examinations. Additionally, the absence of a robust foundation in mathematical fundamentals exacerbates their struggles to navigate the university mathematics curriculum. Consequently, students might find themselves requiring remedial courses or additional support to bridge such knowledge gaps and synchronise with their peers. Jones et al. (2021) attest to the fact that many first-year students lack a strong foundation in essential mathematical concepts, hindering their prospects of success at university level.

Technology and software

Studies underscore how a lack of technological skills can impact first-year university students' understanding of mathematics (Er, 2018). University-level mathematics often necessitates the use of specialised software and technology which may be unfamiliar to students accustomed to traditional learning methods devoid of technological integration. Students who have previously been educated in this way may be less engaged and motivated at university, struggling to maintain enthusiasm for their learning in the absence of interactive and visual learning tools. Additionally, those who were not previously exposed to the new information technologies in their education may be unfamiliar with communications tools and digital collaboration which are crucial for success in academic and professional environments. Brown and Wilson (2019) found that the integration of the new technologies into mathematics education underpins student engagement and comprehension.

Cultural and institutional differences

First-year mathematics students encounter myriad challenges associated with cultural and institutional differences in transitioning to university (Sanagavarapu & Abraham, 2021). Varying approaches to teaching mathematics across different countries and educational systems contribute to a considerable discrepancy in learning methods. For instance, some educational systems may prioritise rote memorisation and examination-based assessments, whereas others emphasise problem-solving and critical thinking skills (Sanagavarapu & Abraham, 2021). This diversity of teaching styles can result in students from different backgrounds facing difficulties in adapting to a new educational environment, which can affect their academic performance. Additionally, cultural differences in learning styles and attitudes towards education can create misunderstandings and conflicts when undertaking group work and/or collaborative learning. Accordingly, it is important to acknowledge and address such disparities to promote equitable academic success.

Research question 2

Examining the literature, several themes and findings were identified in response to the second research question posed by this study: What existing strategies, interventions and programmes have been proposed or implemented to address fragmented mathematics support during the transition period, and what evidence exists regarding their effectiveness?

Addressing challenges with a holistic approach

The present literature review identified several core elements underpinning a holistic approach to mathematics learning, including conceptual understanding; problem-solving skills; active learning; contextualised learning; assessment for learning; cultivating mathematics mindsets; and professional learning communities. Under a holistic approach, it is acknowledged that the entirety of these components surpasses the sum of the individual parts given their intricate interconnectedness and how they affect each other in a systemic way (Toh et al., 2019).

Conceptual understanding

A cornerstone for enhancing mathematical proficiency is conceptual understanding. In order to promote this, students are encouraged to delve into the depths of mathematical concepts (rather than learning through memorisation), a process which fosters in them a robust comprehension that transcends procedural knowledge (Tutak et al., 2011). Students are then able to grasp the fundamental principles and connections inherent in mathematics, thereby facilitating problem-solving and active learning. By employing concrete examples, visual representations, and real-world applications lecturers can illuminate abstract concepts, making them more accessible and tangible. Through this approach, students not only gain a deeper understanding but also develop the ability to transfer their knowledge in diverse contexts.

Problem-solving skills

Mathematics education at the first-year university level may be improved through a process of enhancing students' problem-solving skills (Csapó & Molnár, 2017). By immersing students in a diverse array of challenging and engaging problems, lecturers can cultivate in their students a mindset geared towards critical thinking and analytical competency (Abrami et al., 2015). Encouraging students to explore problems from multiple angles and to develop diverse strategies for creating solutions improves their mathematical skills and fosters their resilience in the face of complex challenges. Teaching explicit problem-solving techniques and fostering reflection on problem-solving processes enables students to navigate the mathematical terrain with confidence and originality. The acquisition of such skills also empowers students to apply mathematical concepts in real-world contexts and to tackle novel problems effectively and creatively.

Active learning

The deployment of active-learning techniques can improve pedagogy and foster students' understanding by fostering their engagement in, and ownership of, the learning process (Ahn & Choi, 2015). By integrating hands-on activities; group discussions; and interactive exercises, educators create dynamic learning environments that encourage students to participate and explore mathematical concepts, rather than simply memorising them. Through active learning, students engage with and apply their knowledge (instead of passively receiving information), leading to deeper conceptual understanding and increased knowledge retention. Active learning also cultivates a positive mathematical mindset by making the subject relevant and approachable.

Contextualised learning

Contextualised learning plays an essential role in strengthening the teaching and learning of mathematics at first-year university level by bridging the gap between abstract mathematical concepts and real-world applications (Madrazo & Dio, 2020). This has been found to foster a deeper understanding of, and appreciation for, the subject.

Assessment for learning

Assessment for learning improves university mathematics education by facilitating continuous monitoring of student progress and understanding (Doño & Mangila, 2021). Undertaking formative assessments, lecturers can dynamically, and in constructive and developmental ways, gauge student comprehension and skills development throughout the learning process. Timely and developmental feedback, which highlights both strengths and areas for improvement, empowers students to reflect on their own learning and make necessary adjustments to enhance their understanding. By engaging in self-reflection and receiving constructive feedback from both peers and lecturers, students develop a better awareness of their strengths and weaknesses, fostering a sense of agency and ownership of their learning.

Cultivating mathematical mindsets

Lecturers' cultivation of positive mathematical mindsets in their students fosters confidence, resilience, and a growth-oriented attitude towards mathematics at the first-year university level (Chisaka, 2019). Promoting a culture of collaboration reinforces positive mathematics mindsets, providing students with opportunities to share ideas, ask questions, and learn from one another.

Professional learning communities

Professional learning communities (PLCs) can play a pivotal role in improving both the teaching and learning of mathematics at first-year university level and comprise a crucial aspect of a holistic approach (Olsson, 2019). By bringing together lecturers, administrators, and stakeholders with a shared commitment to enhancing student outcomes in mathematics education, PLCs create a collaborative environment for the professional growth and development of all participants Through collaborative dialogue and a focus on continuous improvement, PLCs provide educators with opportunities to share best practices, exchange ideas, and engage in reflective discussions about instructional strategies. By leveraging the collective expertise of the community, lecturers can identify and address individual and collective challenges, tailoring teaching methods to meet diverse learning needs.

Research question 3

Examining the literature, several themes and findings were identified in response to the third research question posed by this study: How can a comprehensive synthesis of literature on mathematics support assist in developing a unified framework that effectively addresses the diverse needs and education backgrounds of students engaging in mathematics as they transition from secondary school to university?

This research question was designed with the aim of exploring the possibility of creating a unified holistic approach framework that may enhance first-year university students' performance in mathematics. In this regard, the authors argue that embracing a blend of the core elements of a holistic approach in teaching and learning lays the foundation for a transformative learning experience for students in their first year of mathematics education.

Creating a framework for a unified holistic approach

Figure 2 visually presents the intricate interconnections among the various elements of the proposed holistic approach. Central to this approach is the emphasis on recognising that these elements do not exist in isolation but rather are intricately linked, each influencing and reinforcing the other.

 

 

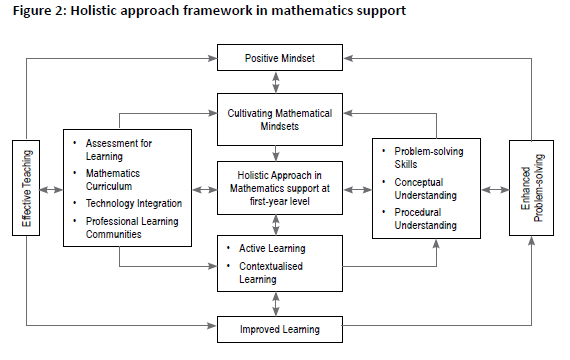
Detailed descriptions and discussions of the components of this holistic approach and their interconnectedness are provided below.

Improved learning

Improved learning outcomes stem from the synergy between active and contextualised learning, which are two interrelated elements of holistic mathematics support for first-year university students. Active learning methods, which have several advantages (Freeman et al., 2014), encourage students to explore mathematical concepts and apply them in various contexts, enhancing understanding and retention (Alkilany, 2017). Meanwhile, contextualised learning embeds mathematical concepts within relevant and meaningful real-world scenarios (Simms, 2016). Combining active and contextualised learning creates a dynamic learning environment which fosters deeper understanding, critical thinking and problem-solving skills among students.

Enhanced problem-solving

Enhanced problem-solving skills result from the interplay between enhanced problem-solving abilities, conceptual understanding, and procedural knowledge as aspects of holistic first-year university mathematics support. Problem-solving skills enable students to tackle complex mathematical challenges using various strategies (Bradshaw & Hazell, 2017). Through practice and exposure to diverse problems, students develop resilience, creativity and critical thinking (Hanfy et al., 2022). Conceptual and procedural understanding enable students to grasp underlying principles and connections between and among mathematical ideas (Juandi & Tamur, 2021), fostering students' confidence in their problem-solving abilities (Al-Mutawah et al., 2019).

Positive mindset

The acquisition of a positive mathematical mindset represents an important goal in the provision of holistic mathematics support at the first-year university level (Simms, 2016). The reciprocal relationship between a mathematical mindset and a positive attitude can underpin student success. As students gain confidence and adopt a growth-oriented attitude, they become more resilient to challenges and setbacks (Hanfy et al., 2022). This positive mindset empowers them to take charge of their education and persevere (Simms, 2016). The interplay between a can-do outlook and belief in one's mathematical ability is reinforced through positive experiences and successes, and supports the establishment of a thriving, inclusive learning environment.

Effective teaching

Effective first-year mathematics support results from the interplay between assessment for learning, the mathematics curriculum, the appropriate integration of technology, and PLCs. Assessment for learning guides educators in tailoring their teaching to student needs by providing timely feedback and highlighting areas for improvement. This feedback informs the development and adaptation of the curriculum so that instructional materials are aligned with learning goals and standards (Al-Mutawah et al., 2019). Meanwhile, PLCs provide support for effective teaching by fostering teamwork and providing a space in which best practices are shared, and ongoing professional development is encouraged (Olsen et al., 2020). This interconnected approach creates a dynamic environment in which educators can deliver high-quality, responsive instruction, and measurably promote student success in mathematics.

 

Discussion

The findings from this survey of the literature highlight the need for a holistic approach in educational institutions to ensure students are prepared for personal fulfilment and professional success, which aligns with the twin goals of promoting student well-being and academic achievement. The review indicates that the challenge of comprehensive mathematics support can only be effectively addressed through recognition of the multifaceted nature of student learning; and that, accordingly, institutions should adopt a holistic approach to support their students' cognitive, emotional, and social development; and, in the process, create a solid foundation for student success.

Against this background, it may be argued that collaborative inquiry initiatives that bridge secondary schools and universities and interrogate the interconnectedness of the factors influencing mathematical proficiency and well-being can play a key role in fostering growth within mathematics education (Jackson & Burch, 2019). By engaging in a process of learning with pupils/students - for example, through a series of reflective dialogues - researchers. academics and university administrators can produce an exchange of ideas; an understanding of best practices; and an evidentiary basis for decision-making and the allocation of resources, so that the mathematics education on offer and the prospects of professional growth among the students are improved.

 

Conclusion

This study highlights the critical need for the adoption by tertiary institutions of a holistic approach to address the multifaceted challenges faced by first-year university mathematics students. The findings indicate that integrating conceptual understanding, problem-solving skills, active learning, contextualised learning, formative assessment of learning, positive mathematical mindsets, and PLCs can lead to the creation of a solid supportive educational environment. Understanding and leveraging the interconnectedness of these elements has been found to significantly enhance students' cognitive, emotional and social development, offering a richer learning experience than that offered by traditional teaching methods.

The study advocates for a shift towards holistic educational practices that prioritise both academic achievement and overall student well-being and prepare students for the complex global challenges that they may face. In addition, collaborative inquiry initiatives that connect secondary schools with universities can play an important role in promoting continuous improvement and innovation in mathematics education. Such initiatives can facilitate the sharing of best practices, resources, and strategies that can help pupils/students in their transition to higher education.

A holistic approach has been found to build students' confidence, creativity and resilience, which are among the characteristics required for academic and personal success - particularly in South Africa, where stark educational and socio-economic disparities persist. By fostering environments that value holistic well-being and academic success, South African universities can better support students in overcoming obstacles and achieving success in mathematics, ultimately empowering students and contributing to their broader success.

 

Acknowledgements

This study was undertaken for Universities South Africa (USAf), an umbrella organization for the 26 public universities in the country, as part of a project entitled Communities of Practice in the Teaching and Learning of Mathematics (CoP TLM). The authors acknowledge the funding contribution received from USAf and the Global Institute for Teacher Education and Society (GITES) for this work.

 

Ethics statement

Strict ethical guidelines were followed in this investigation to guarantee both the study's integrity and the rights of its participants. The study did not directly include actual participants; instead, it analysed the body of current literature. Nonetheless, the following moral guidelines were followed: observance of intellectual property; neutrality and objectivity; openness and replicability; dedication to beneficence and avoidance of harm.

 

Potential conflict of interest

Potential conflicts of interest in the context of this study were unlikely, as the research primarily involved a review of existing literature rather than direct interaction with stakeholders or financial dependencies.

 

Funding acknowledgement

This study was undertaken for Universities South Africa (USAf), which is an umbrella organization for the 26 public universities in the country, as part of a project entitled Communities of Practice in the Teaching and Learning of Mathematics (CoP TLM). The authors acknowledge the funding contribution received from USAf and the Global Institute for Teacher Education and Society (GITES) for this work.

 

References

Abrami, P. C., Bernard, R. M., Borokhovski, E., Waddington, D. I., Wade, C. A., & Persson, T. (2015). Strategies for teaching students to think critically: A meta-analysis. Review of Educational Research, 85(2). https://doi.org/10.3102/0034654314551063        [ Links ]

Adamuti-Trache, M., Bluman, G., & Tiedje, T. (2013). Student success in first-year university physics and mathematics courses: Does the high-school attended make a difference? International Journal of Science Education, 35(17). https://doi.org/10.1080/09500693.2012.667168        [ Links ]

Ahn, H. S., & Choi, Y. M. (2015). The development and application of the augmented reality-based steam education program: Based on the inquiry learning model. International Journal of Applied Engineering Research, 10(10), 27243-27354. https://pure.ewha.ac.kr/en/publications/the-development-and-application-of-the-augmented-reality-based-st-2        [ Links ]

Alkilany, A. (2017). The impact of the use of active learning strategies in the development of mathematical thinking among students and the trend towards mathematics. Journal of Education and Practice, 8(36), 12-18. https://core.ac.uk/download/pdf/234641293.pdf        [ Links ]

Almajed, A., Skinner, V., Peterson, R., & Winning, T. (2016). Collaborative learning: Students' perspectives on how learning happens. Interdisciplinary Journal of Problem-Based Learning, 10(2). https://doi.org/10.7771/1541-5015.1601        [ Links ]

Al-Mutawah, M. A., Thomas, R., Eid, A., Mahmoud, E. Y., & Fateel, M. J. (2019). Conceptual understanding, procedural knowledge and problem-solving skills in mathematics: High school graduates work analysis and standpoints. International Journal of Education and Practice, 7(3). https://doi.org/10.18488/journal.61.2019.73.258.273        [ Links ]

Arif, M. I., & Mirza, M. (2017). Effectiveness of an intervention program in fostering academic resilience of students at risk of failure at secondary school level. Bulletin of Education Research, 39(1), 251-264.         [ Links ]

Arksey, H., & O'Malley, L. (2005). Scoping studies: Towards a methodological framework. International Journal of Social Research Methodology: Theory and Practice, 8(1), 19-32. https://doi.org/10.1080/1364557032000119616        [ Links ]

Bartos, F., Maier, M., Shanks, D. R., Stanley, T. D., Sladekova, M., & Wagenmakers, E.-J. (2023). Meta-analyses in psychology often overestimate evidence for and size of effects. Royal Society Open Science, 10(7). https://www.researchgate.net/publication/372132642_Meta-analyses_in_psychology_often_overestimate_evidence_for_and_size_of_effects        [ Links ]

Berry, E., Mac An Bhaird, C., & Oshea, A. (2015). Investigating relationships between the usage of mathematics learning support and performance of at-risk students. Teaching Mathematics and Its Applications, 34(4), 194-204. https://doi.org/10.1093/teamat/hrv005        [ Links ]

Booth, A., Sutton, A., & Papaioannou, D. (2016). Taking a systematic approach to your literature review. In Systematic approaches to a successful literature review (2nd ed., pp. 9-35). SAGE.

Bradshaw, Z., & Hazell, A. (2017). Developing problem-solving skills in mathematics: A lesson study. International Journal for Lesson and Learning Studies, 6(1), 32-44.         [ Links ]

Bray, A., & Tangney, B. (2017). Technology usage in mathematics education research: A systematic review of recent trends. Computers and Education, 114(C), 255-273. https://doi.org/10.1016/j.compedu.2017.07.004        [ Links ]

Bronfenbrenner, U. (1977). Toward an experimental ecology of human development. American Psychologist, 32(7), 513-531. https://psycnet.apa.org/doi/10.1037/0003-066X.32.7.513        [ Links ]

Brown, J., & Wilson, R. (2019). The role of technology in first-year university mathematics education. Journal of Mathematics Education, 12(3), 245-261.         [ Links ]

Brunton, G., Stansfield, C., Caird, J., & Thomas, J. (2017). Finding relevant studies. In D. Gough, S. Oliver, & J. Thomas (Eds.), An introduction to systematic reviews (2nd ed., pp. 93-122). SAGE.

Chisaka, J. (2019). The use of traditional herbal medicines among palliative care patients at Mulanje Mission Hospital, Malawi [Unpublished master's thesis]. University of Cape Town. https://open.uct.ac.za/items/27556b18-ba2b-4d3c-8891-6224c441bf2c

Csapó, B., & Molnár, G. (2017). Potential for assessing dynamic problem-solving at the beginning of higher education studies. Frontiers in Psychology, 8. https://doi.org/10.3389/fpsyg.2017.02022        [ Links ]

De Jesus, O. N. (2012). Differentiated instruction: Can differentiated instruction provide success for all learners? National Teacher Education Journal, 5(3), 5-11.         [ Links ]

Deeken, C., Neumann, I., & Heinze, A. (2020). Mathematical prerequisites for STEM programs: What do university instructors expect from new STEM undergraduates? International Journal of Research in Undergraduate Mathematics Education, 6(1), 23-41. https://doi.org/10.1007/s40753-019-00098-1        [ Links ]

Doño, M. J. A., & Mangila, B. B. (2021). Mathematics teachers' engagement and students' motivation to learn mathematics. Infinity Journal, 10(2), 285-300. https://www.neliti.com/publications/415080/mathematics-teachers-engagement-and-students-motivation-to-learn-mathematics        [ Links ]

Er, S. N. (2018). Mathematics readiness of first-year college students and missing necessary skills: Perspectives of mathematics faculty. Journal of Further and Higher Education, 42(7), 937-952. https://doi.org/10.1080/0309877X.2017.1332354        [ Links ]

Faulkner, F., Hannigan, A., & Gill, O. (2010). Trends in the mathematical competency of university entrants in Ireland by leaving certificate mathematics grade. Teaching Mathematics and Its Applications, 29(2), 76-93. https://doi.org/10.1093/teamat/hrq002        [ Links ]

Freeman, S., Eddy, S. L., McDonough, M., Smith, M. K., Okoroafor, N., Jordt, H., & Wenderoth, M. P. (2014). Active learning increases student performance in science, engineering, and mathematics. Proceedings of the National Academy of Sciences of the United States of America, 111(23). https://doi.org/10.1073/pnas.1319030111        [ Links ]

Hanfy, H., Daleure, G., Abuquad, K., & Al Hosani, S. (2022). Enhancing critical and creative thinking skills in math at post-secondary level: Examining STEM versus STeM for efficiency and effectiveness. In C. Coombe, L. Hiasat, & G. Daleure (Eds.), English language and general studies in the United Arab Emirates. English language teaching: Theory, research and pedagogy (pp. 129-144). Springer, Singapore. https://doi.org/10.1007/978-981-16-8888-1_9

Hochmuth, R., Broley, L., & Nardi, E. (2021). Transitions to, across and beyond university. In V. Durand-Guerrier, R. Hochmuth, E. Nardi, & C. Winsl0w (Eds.), Research and development in university mathematics education: Overview produced by the International Network for Didactic Research in University Mathematics. Routledge. https://doi.org/10.4324/9780429346859-14

Irons, A., & Elkington, S. (2021). Enhancing learning through formative assessment and feedback (2nd ed.). Routledge.

Jackson, A., & Burch, J. (2019). New directions for teacher education: Investigating school/university partnership in an increasingly school-based context. Professional Development in Education, 45(1), 138-150. https://doi.org/10.1080/19415257.2018.1449002        [ Links ]

Jones, A., Smith, B., & Wilson, C. (2021). Gaps in prerequisite knowledge and their impact on first-year university mathematics students. International Journal of Mathematics Education, 15(2), 102-118.         [ Links ]

Juandi, D., & Tamur, M. (2021). The impact of problem-based learning toward enhancing mathematical thinking: A meta-analysis study. Journal of Engineering Science and Technology, 16(4), 3548-3561.         [ Links ]

Kizito, R., Munyakazi, J., & Basuayi, C. (2016). Factors affecting student success in a first-year mathematics course: A South African experience. International Journal of Mathematical Education in Science and Technology, 47(1), 100-119. https://doi.org/10.1080/0020739X.2015.1057247        [ Links ]

Koskinen, R., & Pitkaniemi, H. (2022). Meaningful learning in mathematics: A research synthesis of teaching approaches. International Electronic Journal of Mathematics Education, 17(2), em0679. https://doi.org/10.29333/iejme/11715        [ Links ]

Madrazo, A. L., & Dio, R. V. (2020). Contextualized learning modules in bridging students' learning gaps in calculus with analytic geometry through independent learning. Journal on Mathematics Education, 11(3). https://doi.org/10.22342/jme.11.3.12456.457-476        [ Links ]

Mayet, R. (2021). Supporting at-risk learners at a comprehensive university in South Africa. Journal of Student Affairs in Africa, 4(2). https://doi.org/10.18820/jsaa.v4i2.2        [ Links ]

Moher, D., Liberati, A., Tetzlaff, J., Altman D. G., & The PRISMA Group (2009). Preferred reporting items for systematic reviews and meta-analyses: The PRISMA Statement. PLoS Med 6(6): e1000097. DOI: 10.1371/journal. pmed1000097        [ Links ]

Mutodi, P., & Ngirande, H. (2014). Exploring mathematics anxiety: Mathematics students' experiences. Mediterranean Journal of Social Sciences, 5(1), 283-294.         [ Links ]

Olsen, J., Lew, K., & Weber, K. (2020). Metaphors for learning and doing mathematics in advanced mathematics lectures. Educational Studies in Mathematics, 105(1), 1-17. https://doi.org/10.1007/s10649-020-09968-x        [ Links ]

Olsson, D. (2019). Improving teaching and learning together: A literature review of professional learning communities. Karlstad University. https://www.diva-portal.org/smash/record.jsf?pid=diva2%3A1341682&dswid=-4881

Page, M. J., McKenzie, J. E., Bossuyt, P. M., Boutron, I., Hoffmann, T. C., Mulrow, C. D., Shamseer, L., Tetzlaff, J. M., Akl, E. A., Brennan, S. E., Chou, R., Glanville, J., Grimshaw, J. M., Hróbjartsson, A., Lalu, M. M., Li, T., Loder, E. W., Mayo-Wilson, E., McDonald, S., & Moher, D. (2021). The PRISMA 2020 statement: An updated guideline for reporting systematic reviews. BMJ 372(71). https://www.bmj.com/content/372/bmj.n71        [ Links ]

Palmer, J. (2016). [Review of the book Redesigning America's community colleges: A clearer path to student success, by Bailey, T. R., Jaggars, S. S., & Jenkins, D.]. Community College Review, 44(1). https://doi.org/10.1177/0091552115606519        [ Links ]

Rach, S., & Heinze, A. (2017). The transition from school to university in mathematics: Which influence do school-related variables have? International Journal of Science and Mathematics Education, 15(7), 1343-1363. https://doi.org/10.1007/s10763-016-9744-8        [ Links ]

Sanagavarapu, P., & Abraham, J. (2021). Validating the relationship between beginning students' transitional challenges, well-being, help-seeking, and their adjustments in an Australian university. Journal of Further and Higher Education, 45(5), 616-628. https://doi.org/10.1080/0309877X.2020.1804537        [ Links ]

Selesho, J. M. (2012). Inclusion of high school learners in the mainstream: Ecological niche. Anthropologist: International Journal of Contemporary and Applied Studies of Man, 14(6), 539-543. http://krepublishers.com/02-Journals/T-Anth/Anth-14-0-000-12-Web/Anth-14-6-000-2012-Abst-PDF/Anth-14-6-539-12-809-Selesho-J-M/Anth-14-6-539-12-809-Selesho-J-M-Tx[6].pmd.pdf        [ Links ]

Shi, Y., Yang, H., MacLeod, J., Zhang, J., & Yang, H. H. (2020). College students' cognitive learning outcomes in technology-enabled active learning environments: A meta-analysis of the empirical literature. Journal of Educational Computing Research, 58(4). https://doi.org/10.1177/0735633119881477        [ Links ]

Simms, V. (2016). Mathematical mindsets: Unleashing students' potential through creative math, inspiring messages and innovative teaching. Research in Mathematics Education, 18(3). https://doi.org/10.1080/14794802.2016.1237374        [ Links ]

Sithole, A., Chiyaka, E. T., McCarthy, P., Mupinga, D. M., Bucklein, B. K., & Kibirige, J. (2017). Student attraction, persistence and retention in STEM programs: Successes and continuing challenges. Higher Education Studies, 7(1), 46-59. https://files.eric.ed.gov/fulltext/EJ1126801.pdf        [ Links ]

Smith, J., & Thomas, R. (2020). The transition from secondary school to university-level mathematics. Mathematics Education Research Journal, 32(4), 513-531.         [ Links ]

Tierney, W. G., & Sablan, J. R. (2014). Completing college: Rethinking institutional action. Journal of Higher Education, 85(2), 280-282. https://doi.org/10.1080/00221546.2014.11777328        [ Links ]

Toh, T. L., Chan, C. M. E., Tay, E. G., Leong, Y. H., Quek, K. S., Toh, P. C., Ho, W. K., Dindyal, J., Ho, F. H., & Dong, F. (2019). Problem solving in the Singapore school mathematics curriculum. In T. L. Toh, B. Kaur, & E. G. Tay (Eds.), Mathematics education in Singapore (pp. 144-164). Springer, Singapore. https://doi.org/10.1007/978-981-13-3573-0_7

Tutak, F. A., Bondy, E., & Adams, T. L. (2011). Critical pedagogy for critical mathematics education. International Journal of Mathematical Education in Science and Technology, 42(1), 65-74. https://doi.org/10.1080/0020739X.2010.510221        [ Links ]

Venezia, A., & Jaeger, L. (2013). Transitions from high school to college. Future of Children, 23(1), 117-136. https://doi.org/10.1353/foc.2013.0004        [ Links ]

Ward, E. G., Thomas, E. E., & Disch, W. B. (2014). Mentor service themes emergent in a holistic, undergraduate peer-mentoring experience. Journal of College Student Development, 55(6), 563-579. https://doi.org/10.1353/csd.2014.0058        [ Links ]

Yoon, S. Y., Imbrie, P. K., Reed, T., & Shryock, K. J. (2018). Identification of the engineering gateway subjects in the second-year engineering common curriculum. International Journal of Engineering Education, 35(1), 232-251. https://www.ijee.ie/1atestissues/Vol35-1A/21_ijee3713.pdf        [ Links ]

 

 

Received 25 September 2024
Accepted 5 December 2024
Published 18 December 2024