Services on Demand
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
South African Journal of Education
On-line version ISSN 2076-3433
Print version ISSN 0256-0100
S. Afr. j. educ. vol.39 n.1 Pretoria Feb. 2019
http://dx.doi.org/10.15700/saje.v39n1a1550
ARTICLES
Pre-service mathematics teachers' mental constructions when using Cramer's rule
Zanele NdlovuI; Deonarain BrijlallII
IDepartment of Mathematics Education, University of KwaZulu-Natal, Durban, South Africa ndlovuz3@ukzn.ac.za
IIDepartment of Mathematics, Durban University of Technology, Durban, South Africa
ABSTRACT
This study explored the mental constructions displayed by pre-service mathematics teachers (PMTs) when applying Cramer's rule. The aim was to reveal the character of mental constructions made around the nature of the solution set of equations and the role of parameters in the solution of equations with parametric coefficients. These mental constructions occur within the Action-Process-Object-Schema (APOS) theory. In this study, data was generated from 31 first year pre-service teachers by means of an activity sheet and interviews. The interviews were used to clarify pre-service teachers' responses to tasks from the activity sheet. The findings revealed that many PMTs displayed procedural understanding of Cramer's rule. It was also found that they understood what the solution of system of linear equations means. This meant that they were operating at the action stage, in terms of APOS. Additionally, it revealed that the lack of construction of related schemata negatively impacted the PMTs' attempt to construct the necessary mental constructions. Therefore, the researchers provided the genetic decomposition (GD) for the use of Cramer's rule to assist teacher educators to analyse the mental constructions of students. This study explored a new application of APOS theory. Analysing the mental constructions of students by means of research is intended to assist in designing alternative teaching strategies. In this way, this study makes a significant contribution to the solution of system of equations pedagogy.
Keywords: APOS; Cramer's rule; parametric coefficients; pre-service mathematics teachers; system of linear equations
Introduction
The knowledge of school mathematics forms a basis for many mathematical topics at undergraduate level. School mathematical knowledge becomes a prerequisite for students to construct coherent frameworks of schemas of the topics they come across at undergraduate level. A particular prerequisite of knowledge needed is the ability to compute (add, subtract, multiply and divide) numbers fluently, and to represent functions algebraically and graphically (Welder, 2006:1). The development of a computation schema is important for the development of other related concepts, such as matrix algebra. Moreover, the development of a function schema is important for the schema development of the solution of a system of equations (Trigueros, Oktag & Manzanero, 2007:2361). Evidently, the study by Kazunga and Bansilal (2017) shows that students who displayed prerequisite knowledge of basic algebra could interiorise a matrix operation into a process. In addition, constructing meaning from procedural methods of solving systems of two equations in two unknowns at school level (2 x 2) is important for understanding the methods of solving a finite number of linear equations consisting of three or more unknowns.
In South Africa, learners encounter a system with two linear equations at Grade Eight. From this level, up to Grade 12, learners learn two methods (elimination and substitution) of solving a 2x2 system of linear equations. At undergraduate level, first year PMTs are expected to generalise school knowledge of solving 2x2 systems of linear equations, to solving n x n systems where n > 3. The introduction of methods such as Cramer's rule and matrix techniques, aims to extend PMTs' school knowledge of the solution of system of equations beyond a 2x2 system, with unique solution, no solution or infinite number of solutions to nxn system of equations.
There is broad agreement in literature that our mental structures or schemas are a key determinant of the level of progress we can achieve in the learning of mathematics (Hong, Thomas & Kwon, 2000). This assumption suggests that having fully developed schemas of any mathematical concept would provide opportunities to make connections between mathematical concepts in the same or unfamiliar contexts. In addition, Hong et al. (2000) have suggested that prior to any pedagogical strategies being considered, the particular concepts that give students difficulty should be analysed empirically. This is to determine the specific mental constructions that a student might make to understand those concepts. Thereafter, "pedagogical strategies need to be developed for students to make the necessary constructions and use them to solve problems" (Dubinsky, 1997:6). Along these lines of thought, the purpose of this study was to analyse and reveal the nature of first year PMTs' mental constructions of solving the system of linear equations with parametric coefficients by using Cramer's rule. We also explored the difficulties associated with their inability to make the necessary mental constructions. We have already explored students' mental constructions of matrices and determinants (Ndlovu & Brijlall, 2015, 2016). Therefore, we now asked the following research question: What insight does an APOS analysis reveal about pre-service mathematics teachers' mental constructions about the nature of the solution of a system when using Cramer's rule? The findings of the study have significant pedagogical implications for PMTs, hence teacher development. We should be mindful of the fact that teachers' actions in classrooms and lecture-rooms have direct consequences on effective learning by students entering the fields of engineering, medicine and commerce. These are vital fields of human resource production that may stimulate the economies of emerging markets. All these fields of study require the knowledge and procedures of matrix algebra and Cramer's rule.
Knowledge Construction of the System of Linear Equations and the Application of Cramer's Rule One of the important aspects involved in the practice and understanding of mathematics is the ability to make connections between concepts and the ability to identify mathematical properties that underlie and describe why a particular method of obtaining the answer was successful (Brijlall & Ndlovu, 2013:16; Usiskin, 2015). The ability to make connections eradicates the external view of mathematics i.e., seeing mathematics as disjointed and learning concepts as isolated facts. Instead, it promotes the view of mathematics as a human activity in which concepts are integrated and reconstructed to make meaning (Jojo, Maharaj & Brijlall, 2013). For example, the understanding of a system of linear equations is embedded in the understanding of several related concepts such as sets, functions, equality, and vector space (Trigueros et al., 2007:2361). Nogueira de Lima and Tall (2008:6) pointed out that the arithmetic algebra played a dominant role in the solution of the system of equations, where the schema development of arithmetic algebra is necessary for the conceptualisation of application techniques used in the solution of system of linear equations. For instance, to understand the application of Cramer's rule, PMT need to have fully developed schema of determinants and matrices, as well as basic algebra. The same was argued by Habgood and Arel (2012:98), namely that accuracies of the solution of system of equations using Cramer's rule depend on the methods used to obtain determinants, and that complexities of Cramer's rule depend exclusively on the determinant calculations. In addition, Egodawatte (2009) has reasoned that for students to develop an understanding of the solution of a system of equations, they first need to construct a schema of variables. The above arguments emphasised that for students to construct conceptual understanding of the solution of a system of equations, they need to conceptualise the techniques used in solving the system and other related concepts.
Students' Difficulties with Knowledge Construction of System of Linear Equations
The knowledge pertaining to a solution of system of linear equations is important because it increases the ability to visualise, describe, and analyse a situation in mathematical terms. Although equations have an important place in the mathematics curriculum, students find them difficult to understand. Trigueros et al. (2007) conducted a study using APOS theory, exploring the difficulties students have with understanding the solution of a finite system of linear equations. The findings showed that the lack of previous knowledge seems to interfere severely with their potential to make the requisite constructions needed to understand new abstract concepts. The study by DeVries and Arnon (2004:58) revealed that the overreliance on memorised rules seems to be the root-cause of students' difficulties. Likewise, Cutz and Kantún (2005) found that students have difficulties understanding the concept of the solution to a system of equations. Dogan-Dunlap's (2010) findings about students' lack of conceptualisation of linear algebra concepts revealed that it mainly emanates from their incorrectly constructed previous schemas. Furthermore, some studies revealed that students, both at school and at undergraduate level, do not construct meaning from the algorithms they use (Brijlall & Ndlovu, 2013; DeVries & Arnon, 2004; Maharaj, 2014; Ndlovu & Brijlall, 2015, 2016). The evidence from the literature cited herein reveals that students' difficulties with a system of linear equations may vary. However, most students harbour a superficial understanding of the required concepts, as well as a limited understanding of the application of techniques used to determine the solution.
The aforementioned studies focus on the difficulties related to students' understanding of the solution of a system of equations, however, there is a lacuna in the literature when it comes to analysing students' construction of the techniques used to determine the solution of the system of equations. Very few studies focus on the use of Cramer's rule in describing the nature of solution/s to a system of linear equations. To this extent, no APOS study has been carried out on the role of parameters on a system of linear equations with parametric coefficients. This study explores these two areas of concern. In this study, Cramer's rule was considered an appropriate method to enhance PMTs' understanding of the solution of a system of equation, since it is an extension of the algorithms of solving a 2x2 system of linear equations learnt at school. Moreover, the application of Cramer's rule to solve a system of linear equations allows for the integration of other concepts, such as matrices and determinants.
Framework Underpinning the Study This study employed APOS theory to describe and analyse PMTs' mental constructions of application of Cramer's rule. The aim of applying APOS theory was to reveal PMTs' mental constructions, and not to provide a comparison of performances. APOS theory is a theory of how mathematical concepts can be learned. In our study, the PMTs are future mathematics teachers and they themselves are currently learning mathematics. In particular, their learning of linear algebra concepts needs to be understood by us (teacher educators). Since APOS theory focuses on models of what might be going on in the minds of these PMTs, we thought that this theory would be ideal to employ in our study. We have used the ideas emanating from APOS theory to formulate a GD, which is provided as a recommendation for future teaching and research. The researchers describe the four stages of learning a mathematical concept that is used in APOS theory for a clear understanding of the analysis of results. The description of the respective concepts of 'action,' 'process,' 'object' and 'schema' used in this study are found in Arnon, Cottrill, Dubinsky, Oktac, Fuentes, Trigueros and Weller (2014:19-25).
Action
An action "... is [an] externally directed transformation of a previously conceived object(s). It is external in the sense that each step of the transformation needs to be performed explicitly and guided by instructions, each step cannot yet be imagined and none can be skipped" (Arnon et al., 2014:19). An example of this (from the given tasks) is when a student was given a system of η χ m equations, and was asked whether the system can be solved using Cramer's rule. At an action level, the student would undertake a step-by-step procedure of solving the system using Cramer's rule, before attempting to answer the question. Alternatively, the student would guess the answer with no explanation. Another example is to consider a system of equations with literal coefficients. At an action level, students will substitute these coefficients with numerals before applying Cramer's rule, or before deciding whether the solution exists or not.
Process
Arnon et al. (2014:21) note that "As actions are repeated and reflected upon, the individual moves from relying on external cues to having internal control over them. This is characterised by an ability to imagine carrying out the steps without necessarily having to perform each one explicitly." An example of this stage (from the tasks), occurs if the student predicts the outcome, and provides a clear explanation in relation to the application of Cramer's rule. An individual is able to imagine the structure of a system of linear equations, to which Cramer's rule can be applied.
Object
Arnon et al. (2014:21) note that "This occurs when an individual applies an action to a process that sees a dynamic structure as a static one to which actions can be applied." At this stage, a student can describe how a given solution appears, multi-represent and interpret it. In addition, consider a system Ax = b, such that |i4| Φ 0. When a student can perform actions on |^| to find the values of the literal coefficient that makes the system inconsistent, we say the object understanding has developed.
Schema
Arnon et al. (2014:25) write that "schemas are structures that contain the descriptions, organisation, and exemplifications of the mental structures that an individual has constructed regarding a mathematical concept." A schema is an individual's collection of actions, processes, objects, and other schemas, which are linked by some general principles to form a framework in the individual's mind that may be brought to bear upon a problem situation involving that concept. If an individual is asked to determine the solution of a system using Cramer's rule, at this stage of learning, the individual will bring together various mental constructions and other schemas to address this task; such as the process conception of the determinant, matrix schema, schema of other related algorithms, and a schema for basic algebra. The basic algebra schema would have developed during the learning of school mathematics. It ought to include the process conceptions of operations involving real numbers, relating the system of linear equations to the structure of the solution, relating solution structure to the algorithms, as well as relating symbolic to geometric representation.
Methodology
We adopted a case study design involving a group of pre-service mathematics teachers in their first year of study. In the case study, the main assumption is that the phenomenon is investigated as a bounded system. This system may be a group of people (Creswell, 2007). In our case, the bounded system was a group of PMTs participating in an activity around Cramer's rule in a linear algebra course for PMTs. Since our study involved a small group of PMTs the results cannot be generalised. A case study was considered appropriate since the aim was to gain an in-depth understanding of pre-service teachers' mental constructions of Cramer's rule, as one of the tools to solve systems of equations. Although, at the initial stage, the analysis of the response could be categorised as statistical, the data presented here is mainly qualitative. Thirty-one PMTs participated in the study. During lecture times, PMTs were taught the application of Cramer's rule to solve a system of linear equations. This section was taught over four lecture periods of 45 minutes each. A subsequent homework task was followed by a 90-minute tutorial session, in which students had to individually work on an activity sheet. Group and class discussions would then follow. Once the activity sheets were analysed, themes emerged which helped the researchers to categorise the responses, and interviews followed to verify what transpired in the written responses.
Validity and Reliability
According to Cohen, Manion and Morrison (2007:149), "reliability in qualitative research can be regarded as between what researchers record as data and what actually occurs in the natural setting that is being researched." In our study, the PMTs were taught, and responded to the research instruments in the lecture rooms. Creswell (2007) maintains that reliability can be addressed in several ways in qualitative research, such as obtaining detailed field notes, and employing good quality tape for recording and transcribing. This study uses interviews as one of the data collection methods, which were tape recorded and transcribed to ensure reliability. In qualitative methodologies reliability includes fidelity to real life, context and situation, specificity, authenticity, comprehensiveness and meaningfulness to the respondents (Cohen et al., 2007). The PMTs in our study were assured that the data collected would not be divulged to anyone, except university structures, and it would be kept safely by the university. If participants elected to read the information before it was made public, they would be free to do so. This would also increase the trustworthiness of the study. The activity worksheets have been used in the pilot study. The aim was to test the instrument to ensure that it generated the required data. This study addressed the issue of reliability and trustworthiness through triangulation of data collection methods. Data was collected using different methods, namely, individual written responses, classroom discussion, interviews to verify the written responses, and researcher interpretation of mental constructions made from written responses.
Data Analysis
The focus of the research was to understand the nature of the mental constructions made by PMTs when solving the system of equations using Cramer's rule. The structures APO (Action-Process-Object), as explained in APOS theory, assisted in determining appropriate categories by means of which to understand the mental constructions made. APO, together with Table 1, provided a means to carry the analysis of students' responses.
Findings
The activity sheet consisted of two questions, as shown in the above table. In this study, the questions are presented as items. The categorisation of written responses for each of the items is given in Table 2.

Item 1 was intended to determine whether the PMTs would first check the conditions for the application of Cramer's rule. It was surprising that no PMT mentioned that Cramer's rule cannot be used to solve this system of linear equations simultaneously, since there were more equations than variables. The analyses of written responses for Item 1 revealed that 22 students had difficulties in thinking about the solution without solving the system. They could not predict the outcome or provide a clear explanation as to why it was not possible to solve the system using Cramer's rule. They struggled to coordinate their understanding of the application of Cramer's rule and the type of solution the system ought to produce. The lack of process-conception of the determinant contributed to their inability to make connections between the type of system, the type of solution and application of Cramer' rule. The findings showed that algorithm was instrumentally understood, thus the PMT struggled to conceptualise the application of the algorithm beyond carrying out procedures. Therefore, they could not make the connection between the structure of the system of linear equation and application of Cramer's rule.
Of the 31 participants, nine made connections between the system of equations and the application of Cramer's rule, suggesting that they had developed the process conception of the application of Cramer's rule. They interpreted the system and internally made a connection between the type of system and the application of Cramer's rule, without having to perform the step-by-step calculation. Their responses showed that the action of constructing the coefficient matrix as a representation of the system of equations was interiorised. Zinhle and Thabo's written responses showed the evolution of their thinking processes about the application of Cramer's rule. Zinhle transformed the system into a coefficient matrix (see Extract 1). Her response showed that she had interiorised the action into a process, because she related the system of linear equation to matrix and could explain the matrix order. She constructed a coefficient matrix, which helped her realise that the given system was a nonsquare matrix and that the determinant was undefined. The action-conception of the matrix order has been interiorised into a process as she could relate the matrix order to the application of Cramer's rule, and relate the matrix order to the evaluation of determinant. Zinhle coordinated the process of verifying the determinant with the process of the type of the system to explain the lack of possibility of applying Cramer's rule in the system in question.

Zinhle verbally described the procedures needed to solve the system using Cramer's rule and the restrictions thereof without performing each step. This meant that she has constructed the collection of all the necessary rules and understanding of all the procedures (see Extract 2).

As evident in the written response, the action of determining the order has been interiorised, which makes it possible for Zinhle to relate the matrix structure to linear equation system structure to which Cramer's rule can be applied. A similar case ensued with Thabo (see Extract 3).

He imagined all the actions internally and the constraints associated with the application of Cramer's rule with the purpose of deducing the existence/non-existence of a solution to this system of linear equations. These findings are included in the GD formulated and presented in the recommendations section.
Item 2 was intended to determine whether PMTs would solve the parametric system of equations, and whether they could explain the meaning of the solution in its abstract form. Four PMTs did not answer Item 2a. Therefore, their non-responses were not included in the analysis. Similarly, in Item 2b, 10 PMTs did not attempt the question, including the four in Item 2a, and nine provided incorrect responses.
Item 2a considers a typical system of equations with a unique solution for  In this item, PMTs who have cognitively constructed the process of applying Cramer's rule to solve the system of linear equations with numerals as co-efficients would be able to use that same knowledge to find the solution to parametric equations. Secondly, participants with the notion of a variable as a mathematical object, and process understanding of Cramer's rule and solution set, should be able to solve the given problem. Of the 22 students operating at the action stage in Item 1, four did not attempt Item 2a. While in Item 1 they showed action-conception of Cramer's rule, it seems the action-conception had not fully developed because they couldn't carry out the necessary procedures to solve the system. Some PMTs operating at action level carried the necessary steps, but the lack of computational fluency led to incorrect answers. Others showed that their knowledge of the application of Cramer's rule and the meaning of the solution was limited to concrete system only. This was evident since they replaced parameters with numerals. During the interview with Thula, he said,
In this item, PMTs who have cognitively constructed the process of applying Cramer's rule to solve the system of linear equations with numerals as co-efficients would be able to use that same knowledge to find the solution to parametric equations. Secondly, participants with the notion of a variable as a mathematical object, and process understanding of Cramer's rule and solution set, should be able to solve the given problem. Of the 22 students operating at the action stage in Item 1, four did not attempt Item 2a. While in Item 1 they showed action-conception of Cramer's rule, it seems the action-conception had not fully developed because they couldn't carry out the necessary procedures to solve the system. Some PMTs operating at action level carried the necessary steps, but the lack of computational fluency led to incorrect answers. Others showed that their knowledge of the application of Cramer's rule and the meaning of the solution was limited to concrete system only. This was evident since they replaced parameters with numerals. During the interview with Thula, he said,
"There were too many variables so I had to let k be a number so I [could] solve for x and y."
The response shows that Thula has not constructed the difference between variables and literal coefficient. The incorrect notion of variables prevented Thula from being able to internalise the application of Cramer's rule.
Another premise with Item 2a was that PMTs with the process conception of Item 1 should also have the process conception of Item 2a. On the contrary, the findings showed that five students -seemingly with the process-conception of Cramer's rule in Item 1 - were operating at the action level in Item 2a. The findings showed that while some PMTs seem to have constructed the process-conception of the constraints associated with application of Cramer's rule, their knowledge was characterised by memorised facts and not understanding of the concept. These findings are included in the GD formulated and presented in the Recommendations section. The five participants struggled to apply Cramer's rule to parametric equations, thus opting to reduce the equation to concrete form. The difficulties displayed by these participants are not related to the application of Cramer's rule, but to the solution of system of linear equations. At the school level, students deal with only concrete systems of equations. Therefore, the lack of the development of an equation schema and the process understanding of the meaning of the solution set made it difficult for these PMTs to solve the parametric system. Below is an extract showing some students difficulties with solving parametric equations.
This response was categorised at the action level. However, in Item 1, Jack's response showed that he had a process conception of Cramer's rule. Jack substituted k with 2 and carried out the procedures to solve the system of equations. His response showed that the solution set was conceptualised in terms of the numerals. While he understood the application of Cramer's rule, his understanding of the solution set of a system of linear equations is limited to a concrete system only.
The response showed that Jack's focus was on applying the rule and solve for the unknowns (see Extract 4). He has no conception of the meaning of the solution set. The findings show that the lack of understanding the type of system to which Cramer's rule can be applied did not help participants make connections between the rule and solution set. It is evident that Jack has the action conception of Cramer's rule, but has not internalised it to

understand the meaning of the solution set (see Extract 5).

Eight students constructed the necessary mental constructions needed for the development of an object understanding of the application of the solution set. Their responses indicated a coherent understanding of the collection of rules and could apply them accordingly.
Thabo's written response (see Extract 6) indicated he had encapsulated the process of constructing the coefficient matrix as a representation of the system of the equation into objects to which certain actions, and other processes such as evaluating determinants, were performed. Thabo solved the system in its abstract form, thus showing the conceptualisation of the rule. He encapsulated the parameters as mathematical objects. This, we observed, since he generalised his knowledge of solving the system of equations to unfamiliar contexts, without trying to reduce the abstract nature of the problem. This was verified through an interview in Extract 7.


This response had some indicators, which showed that Thabo had encapsulated the process understanding the solution set because he could make connections between the algorithm used, other concepts such as determinants, and the type of system of equations. The processes constructed were coordinated to determine the solution set and understand the meaning of the solution in relation to the given system.
The process conception of Cramer's rule allowed him to encapsulate the meaning of the solution to an object level. He could imagine how the solution ought to be by analysing the features of the system and multi-represent the solution. However, this imagination had a shortfall when he used the idea of gradients of the two lines. We know that 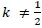 for the determinant of the coefficient 2 matrix to be defined. The gradients of the two lines
for the determinant of the coefficient 2 matrix to be defined. The gradients of the two lines  are
are 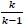 and
and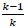 . So, k ≠ 0 and k ≠ 1 for the gradients to be well defined. The gradients of the two lines are unequal
. So, k ≠ 0 and k ≠ 1 for the gradients to be well defined. The gradients of the two lines are unequal 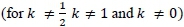 ,hence the two lines are not parallel and will intersect showing us a unique solution can exist. Thabo lacked this argument.
,hence the two lines are not parallel and will intersect showing us a unique solution can exist. Thabo lacked this argument.
In Item 2b, PMTs with a process understanding of the application of Cramer's rule and meaning of the solution would perform the necessary manipulations on the determinant of the coefficient matrix to determine the type of system. From the analysis of written responses, 19 PMTs showed lack of equation schema, thus some did not attempt the question and others provided incorrect responses. The findings showed that these PMTs could not have constructed the understanding of different types of systems and meaning of the solution set. The results further revealed that PMTs with the process or object conception of Item 2a managed to solve 2b as expected. They understood that the determinant of zero makes the system inconsistent, since division by zero is undefined.
The interview below showed that only when connection between concepts are made then conceptual understanding of the concept is possible.
Zinhle reflected on her school knowledge of analytic geometry and related it to the procedures needed in the application of Cramer's rule, to develop her understanding of the meaning of her solution. She has internalised procedures associated with Cramer's rule and coordinated the process of division and of evaluating the determinant to construct a new process of evaluating the type of system. Moreover, in Extract 8, we observe that she displayed a coherent understanding of collection rules and application of such rules in constructing a meaningful understanding of the concepts.

These findings are included in the GD formulated and presented in the recommendations section. Thabo also showed the object-conception of the solution set. He performed actions and processes to transform the 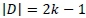 to determine the value of k. From the interview response below, we observe that Thabo determined the conditions of application of Cramer's rule, the conditions of consistent and inconsistent system of linear equation in relation to Cramer's rule, and used it to construct the understanding of the solution of the system of equations and the algorithms used to solve it. In addition, we observe in Extract 9 that he showed conceptual understanding of other related algorithms that could be used in relation to Cramer's rule to solve the system of equations.
to determine the value of k. From the interview response below, we observe that Thabo determined the conditions of application of Cramer's rule, the conditions of consistent and inconsistent system of linear equation in relation to Cramer's rule, and used it to construct the understanding of the solution of the system of equations and the algorithms used to solve it. In addition, we observe in Extract 9 that he showed conceptual understanding of other related algorithms that could be used in relation to Cramer's rule to solve the system of equations.

Discussion
The purpose of this research was to explore PMTs' mental constructions of the application of Cramer's rule to solve a system of linear equations with parametric coefficients. APOS analysis allowed researchers to understand and explain the level at which pre-service teachers were operating with regard to the solution of system using Cramer's rule. This study has therefore contributed to the application of APOS theory in this topic, which has not been done before. Our analysis shows how APOS theory can be used in making conclusions at the level of conception that the PMTs were. The analysis of the data has helped us identify significant areas which need consideration, and therefore has serious pedagogical implications internationally, as Cramer's rule is taught in all standard Mathematics courses throughout the world. This topic is fundamental to any undergraduate studies for students entering the fields of engineering, commerce and medicine. These fields of expertise have strong relevant bearing for rapid economic growth in emerging economies like South Africa. It is found that besides natural resources, human resources are highly necessary for economic development in emerging nations (Anderson & Strutt, 2013). The findings in our study showed that many PMTs had an action-conception of Cramer's rule, and the meaning of the solution of a system of equations. Furthermore, PMTs who had the action-conception in Item 1 displayed the action conception in all the items, indicating that they had constructed a procedural knowledge of the algorithm. Therefore, for such PMTs, the instructions should be aimed at helping them interiorise the procedures using a concrete system of equations, before introducing parametric equations.
As literature states, prerequisite knowledge plays an important role in the construction of new knowledge (Bansilal, Brijlall & Trigueros, 2017; Ndlovu & Brijlall, 2015:12, 2016:150; Trigueros et al., 2007). It was evident from the results that the lack of prerequisite knowledge impacted negatively on PMTs' understanding of Cramer's rule, and the meaning of the solution. For example, the lack of basic algebra, real number system and understanding of the order of the system, caused difficulties in the respondents' attempts to explain the type of system that could be solved using Cramer's rule. The findings concur with Cutz and Kantún (2005), who identified the lack of understanding of related concepts as the main cause of the difficulties students have with conceptualising the system of equations. It was evident that for many PMTs, the rule was instrumentally understood and therefore, it hindered the determination of the solution of the system and constructing the meaning of the solution. Thus, for some PMTs, the meaning of a solution is constructed in terms of numerals. Therefore, they struggle to solve parametric equations. The results further revealed that when concepts are understood as isolated facts, they delay the development of the required schemata. In this case, the variable schema, equation schema, as well as meaning of the type of system schema, are necessary for the development of the meaning of the solution of a system and the application of the Cramer's rule schema. However, the results showed that for many PMTs, the connection between these concepts has not developed. The findings above have immense pedagogical implications, as they show a PMT's understanding of the solution of system of equations using Cramer's rule is at surface level. It is therefore imperative to use alternative teaching strategies to assist students to conceptualise the concepts.
Conclusion and Recommendations
To answer our research questions, it was evident that the difficulties students have with the application of Cramer's rule were caused by the lack of previous construction needed in the development of the concepts. To this end, the lack of determinant, function, understanding parameters and the lack of a matrix schema all impacted negatively in the knowledge construction of Cramer's rule and solution system. Secondly, Cramer's rule is an algorithm used to solve a system of linear equations, therefore, if the meaning of the solution set is not constructed, it will affect students' construction of the rule. Thirdly, memorisation of algorithms caused students to fail to interiorise actions into the process and to encapsulate process into objects, thus failing to conceptualise the taught concepts. What was more noticeable in the students' responses was that, for many students, the reasoning about Cramer's rule is concrete. They can only solve the system with numerals as coefficients and that their thinking of the solution set is associated with numerals only. It was further noticeable that PMTs whose conception was limited to an action level, could not interiorise the action into process and encapsulate to an object. Thus, most pre-service teachers could not construct the schema of the solution of system of equations.
The tasks used to understand the mental construction of the application of Cramer's rule did not include the object understanding of the algorithm. We therefore recommend further research focusing on mental constructions of Cramer's rule. Within this focus the prerequisite knowledge for this topic needs to borne in mind (see Figure 1). Understanding mental constructions of the algorithms would possibly explain the reasons for the difficulty displayed by many PMTs with the meaning of the solution. To contribute to the pedagogy of the solution of system of equations using Cramer's rule, the researchers provide the genetic decomposition (see Figure 2) that could be used by teacher educators to analyse students' mental constructions of these concepts before deciding on any instructional strategies. As pointed out in the literature, analysing students' difficulties by means of research, it is necessary for planning alternative teaching strategies (Dubinsky, 1997). With this in mind, the researchers design a genetic decomposition for a possible solution for a system of equations and Cramer's rule as contribution to APOS theory and to the teaching of the concepts.

Authors' Contributions
ZN proposed the study and collected the data. DB and ZN carried out the analysis and ZN proposed the initial genetic decomposition and DB refined the genetic decomposition. ZN was the corresponding author.
Notes
i. In the student solution, it is represented as |D |.
ii. Published under a Creative Commons Attribution Licence.
References
Anderson K & Strutt A 2013. Emerging economies, productivity growth, and trade with resource-rich economies by 2030. Paper presented at the 57th AARES Annual Conference, Sydney, 5-8 February. [ Links ]
Arnon I, Cottrill J, Dubinsky E, Oktaf A, Fuentes SR, Trigueros M & Weller K 2014. APOS theory: A framework for research and curriculum development in mathematics education. New York, NY: Springer. https://doi.org/10.1007/978-1-4614-7966-6 [ Links ]
Bansilal S, Brijlall D & Trigueros M 2017. An APOS study on pre-service teachers' understanding of injections and surjections. The Journal of Mathematical Behavior, 48:22-37. https://doi.org/10.1016/j.jmathb.2017.08.002 [ Links ]
Brijlall D & Ndlovu Z 2013. High school learners' mental constructions during solving optimisation problems in Calculus: A South African case study. South African Journal of Education, 33(2): Art. #679, 18 pages. https://doi.org/10.15700/saje.v33n2a679 [ Links ]
Cohen L, Manion L & Morrison K 2007. Research methods in education (6th ed). New York, NY: Routledge. [ Links ]
Creswell JW 2007. Qualitative inquiry and research design: Choosing among five approaches (2nd ed). Thousand Oaks, CA: Sage. [ Links ]
Cutz Kantún BM 2005. Un estudio acerca de las concepciones de estudiantes de licenciatura sobre los sistemas de ecuaciones y su solution [A study about the conceptions of undergraduate students about the systems of equations and their solution]. MEd thesis. Cinvestav, Mexico: University of Mexico. [ Links ]
DeVries D & Arnon I 2004. Solution - What does it mean? Helping linear algebra students develop the concept while improving research tools. In Proceedings of the 28th Conference of the International Group for the Psychology of Mathematics Education (Vol. 2). Available at http://www.kurims.kyoto-u.ac.jp/EMIS/proceedings/PME28/RR/RR211_Arnon.pdf. Accessed 20 November 2018. [ Links ]
Dogan-Dunlap H 2010. Linear algebra students' models of reasoning: Geometric representations. Linear Algebra and its Application, 432(8):2141 -2159. https://doi.org/10.1016/j.laa.2009.08.037 [ Links ]
Dubinsky E 1997. Some thoughts on a first course in linear algebra at the college level. In D Carlson, CR Johnson, DC Lay, AD Porter, A Watkins & W Watkins (eds). Resources for teaching linear algebra (MAA Notes, Vol. 42). Washington, DC: Mathematical Association of America. [ Links ]
Egodawatte G 2009. Is algebra really difficult for all students? Acta Didacta Napocensia, 2(4):101 -106. Available at https://files.eric.ed.gov/fulltext/EJ1052268.pdf. Accessed 13 November 2018. [ Links ]
Habgood K & Arel I 2012. A condensation-based application of Cramer's rule for solving large linear system. Journal of Discreet Algorithms, 10:98-109. https://doi.org/10.1016/jjda.201L06.007 [ Links ]
Hong YY, Thomas M & Kwon ON 2000. Understanding linear algebraic equations via super-calculator representations. In T Nakahara & M Koyama (eds). Proceedings of the 24th conference of the International Group of Psychology of Mathematics Education. Washington, DC: ERIC Clearinghouse. Available at https://www.math.auckland.ac.nz/~thomas/index/staff/mt/My%20PDFs% 20for%20web%20site/PME00YY.pdf. Accessed 20 November 2018. [ Links ]
Jojo ZMM, Maharaj A & Brijlall D 2013. From human activity to conceptual understanding of the chain rule. Journal of Research in Mathematics Education, 2(1):77-99. [ Links ]
Kazunga C & Bansilal S 2017. Zimbabwean in-service mathematics teachers' understanding of matrix operations. The Journal of Mathematical Behavior, 47:81-95. https://doi.org/10.1016/jjmathb.2017.05.003 [ Links ]
Maharaj A 2014. An APOS analysis of natural science students' understanding of integration. Journal of Research in Mathematics Education, 3(1):54-73. https://doi.org/10.4471/redimat.2014.40 [ Links ]
Ndlovu Z & Brijlall D 2015. Pre-service teachers' mental constructions of concepts in matrix algebra. African Journal of Research in Mathematics, Science and Technology Education, 19(2):156-171. [ Links ]
Ndlovu Z & Brijlall D 2016. Pre-service teachers' mental constructions of Determinant concept. International Journal of Education Studies,14(1,2):145-156. [ Links ]
Nogueira de Lima R &Tall D 2008. Procedural embodiment and magic in linear equations. Educational Studies in Mathematics, 67(1):3-18. https://doi.org/10.1007/s10649-007-9086-0 [ Links ]
Trigueros M, Oktaj A & Manzanero L 2007. Understanding of systems of equations in linear algebra. In D Pitta-Pantazi & G Philippou (eds). Proceedings of the Fifth Congress of the European Society for Research in Mathematics Education. Larnaca, Cyprus: European Society for Research in Mathematics Education (ERME). [ Links ]
Usiskin Z 2015. What does it mean to understand some mathematics? In SJ Cho (ed). Selected regular lectures from the 12th International Congress on Mathematical Education. Cham, Switzerland: Springer. https://doi.org/10.1007/978-3-319-17187-6 [ Links ]
Welder RM 2006. Preservice elementary teachers' mathematical content knowledge of prerequisite algebra concepts. PhD Dissertation. Bozeman, MT: Montana State University. Available at http://citeseerx.ist.psu.edu/viewdoc/download?doi= 10.1.1.427.9428&rep=rep1&type=pdf. Accessed 11 November 2018. [ Links ]
Received: 13 July 2017
Revised: 21 July 2018
Accepted: 15 December 2018
Published: 28 February 2019














