Services on Demand
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
South African Journal of Childhood Education
On-line version ISSN 2223-7682
Print version ISSN 2223-7674
SAJCE vol.4 n.3 Johannesburg 2014
ARTICLES
Foundation phase teachers' (limited) knowledge of geometry
Kakoma Luneta*
University of Johannesburg
ABSTRACT
This study is about student teachers' conceptual understanding of shapes. While the National Curriculum Statement stipulates that by the time learners exit high school they should have grounded knowledge of basic geometry and know shapes such as polygons and polyhedrons and their properties, this study finds that the majority of student teachers have limited knowledge of basic geometry and require not remedial, but re-learning of these basic concepts. The Van Hiele levels of geometric thought model is used as a lens to gauge and understand students' knowledge of geometry. A cohort of 128 first-year students registered for a foundation phase programme took part in the study. It was found that while Grade 12 learners are expected to operate at levels 3 and 4 of the Van Hiele's levels, the majority of the participants in the study were operating at level 1, the level of the learners they will be teaching when they complete the course. Suggestions are made for how to address this problem.
Keywords: Geometry, shapes, polygon, polyhedrons; geometric thoughts, Van Hiele's levels of geometric thought
Introduction
Geometry - the "study of shapes, their relationships, and their properties" (Bassarear 2012:463) - has a long history arising from the practical measurement of land in ancient Egypt and the study of the properties of shapes in Greek geometry (Cooke 2007). It has been said that geometry is the field of mathematics that offers the "enormous potential of bringing the subject alive" (Chambers 2008:187). It is an exploratory field of mathematics that has links with culture, history, art and design, and its interactions with these vital human constructs provide opportunities to make geometry lessons interesting and stimulating (ibid). In this study, 'basic geometry' refers to polygons, polyhedrons and their properties, as opposed to 'coordinate' or 'analytical geometry', which not only requires geometric knowledge but also knowledge in working with coordinates on a 2-D (two-dimensional) or 3-D (three-dimensional) set of axes. These added concepts render geometry more complex and require a more accomplished manner of thinking. Van de Sandt (2007:2) concedes that geometry is regarded as a "problematic topic" at secondary schools in South Africa. One of the main reasons for this is that teachers and learners operate and communicate at different Van Hiele levels of learning, which impairs the latter's understanding of critical concepts in geometry (Pusey 2003).
Piaget (1952) argued that children's geometric understanding develops with age and that in order for children to create ideas about shapes, they need to interact physically with objects. Clements, Swaminathan, Hannibal and Sarama (1999:193) asserted that "children's representation of space is constructed through the progressive organisation of the child's motor and internalised actions". Van Hiele (1986; 1999), on the other hand, analysed various aspects involved in the learning of geometry, such as teachers trying to communicate at the same levels as learners. Van Hiele agreed with Piaget that children think geometrically at different levels during their cognitive development (Pusey 2003).
The purpose of this study was to investigate the knowledge of geometry with which student teachers enter university. It was a predominantly qualitative study that used interpretive descriptions to analyse the data obtained and Van Hiele's levels of geometric thought as a gauge. The research question was: What knowledge of basic two- and three-dimensional shapes do foundation phase student teachers have at the time they enter the university programme?
Geometry: Recognising spatial relationships
Geometry deals with the spatial relationships between real things. Knowledge of geometry and geometric reasoning is not acquired through passive consideration, but rather through active interaction with and exploration of shapes (Clements & Sarama 2000). According to Frobisher, Frobisher, Orton and Orton (2007:19), "in their learning of shapes and space children experience and understand the connections between knowledge, concepts and skills in the different facets of geometry". This means that teachers should be mindful of a child's environment and adapt their instructional approach to teaching geometry by employing a more practical approach that draws on a child's sense of space (or spatial sense), which is defined as the understanding of shapes by describing their characteristics and their relations to each other (Battista 2007). Spatial sense consists of two important components of geometric knowledge, namely spatial visualisation (the ability to visually compare shapes that have changed position on the plane (for two-dimensional shapes) or in space (for three-dimensional shapes)), which is essentially transformation geometry (Bassarear 2012), and spatial orientation, which operates when a fixed object is viewed from different points or when the position of an object is acknowledged (Battista 2007).
These two components of geometric knowledge play an important role in learners' ability to understand shapes and their properties through geometric reasoning and visualising the images, their properties and physical representations. With well-reasoned and well-executedinstruction, learners can use geometric reasoning -defined as "the invention and use of formal conceptual systems to investigate shapes and space" (Battista 2007:843) - to solve geometric problems as they develop their understanding of geometry. Spatial sense is informed by spatial reasoning, which, according to Bahr, Bahr and De Garcia (2010:390), is at the heart of all mathematical strands and comprises "the ability to think and reason by comparing, manipulating and transforming a mental picture".
Learners use spatial reasoning to analyse and compare shapes, estimate quantity, and make mental computations. Hence the knowledge of shapes should not revolve around merely knowing their names, but rather around thinking in geometric contexts: shapes (level 0); properties (level 1); informal logic (levels 2 and 3); and deductive principles about shapes (level 4) (Frobisher et al 2007). Instruction should be built on content knowledge that is appropriate for the various levels of knowledge, and activities should be designed to challenge learners at the next level. For instance, learners at level 0 can be encouraged to provide the properties of shapes, while those at level 1 should be encouraged to formulate and engage in deductive reasoning.
Van Hiele (1999; 1986) proposed five levels of geometric thought (Bahr et al 2010; Musser, Burger & Peterson 2011). For Van Hiele, learners progress and develop their knowledge of geometry in accordance with the developmental trajectory suggested by these levels. On level 0, (visualisation/recognition), learners can identify a shape, but they are unable to list its properties and typically judge the shape by its appearance. On level 1 (analysis), which is a largely descriptive level, learners are able to identify the properties of particular shapes, but not in logical order. On level 2 (abstraction/relationships), which is an informal deductive level, learners can combine shapes and their properties to provide a precise definition, as well as relate shapes to other shapes. They can also present a logical ordering of the properties and these are deduced from one another. On level 3 (deductive), learners apply formal deductive arguments such as proofs and theorems within an axiomatic system. Level 4 (rigor/ axiomatics), also known as the metamathematical level, is characterised by "formal reasoning about mathematical systems by manipulating geometric statements such as axioms, definitions, and theorems" (Van de Sandt 2007:1). Learners at this level of geometric thought can also "compare systems based on different axioms and can study various geometries in the absence of concrete models" (Burger & Shaughnessy 1986:31). Learners in primary school are not expected to operate at this level.
Understanding these levels enables teachers to identify the general direction of their students' learning and the level at which they are operating geometrically. The first three levels show the development of procedural fluency in geometry and the last two the development of conceptual understanding (Kilpatrick, Swafford & Findell 2001). Van Hiele's theory is divided into two parts. The first concerns the hierarchical sequence of the levels, which holds that learners must develop each one fully before proceeding to the next, and the second the development of intuition in learners and the phases of learning that influence geometry learning. To date, Van Hiele's theory of geometric thought is regarded as the best framework known for teaching and learning geometry (Mayberry 1983; NCTM 2000; Wu & Ma 2006).
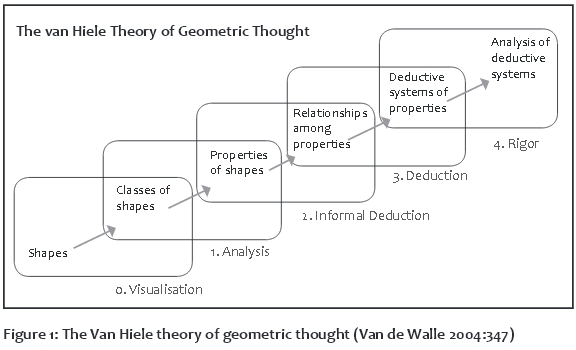
Van Hiele's levels provide teachers with a frameworkin which to conduct geometric activities by designing them with the assumptions of a particular level in mind. It also allows them to ask questions that are below or above a particular level (Van de Walle 2004). Van Hiele's (1986) theory of geometric knowledge, with its focus on geometric reasoning, has been linked to Piaget's five stages of child development in terms of the role they play in learning geometry (Pusey 2003). However, Van Hiele's levels of geometric knowledge are not age-specific or age-dependant, which suggests that learners' progression from one level to the next is dependent on the effectiveness of the teaching and content acquisition opportunities that they are exposed to (Frobisher et al 2007).
By the time learners graduate from high school they should have acquired a substantial understanding of basic geometry. School curricula worldwide from Grade R (reception) to Grade 12 cover four main learning outcomes in geometry (Bahr et al 2010; Bassarear 2012; RSA DBE 2010). On completion of Grade 12, learners should be able to:
• Analyse the characteristics, properties and relationships of two- and three-dimensional geometric shapes (Euclidean geometry) (which is predominantly what primary school mathematics curricula set out to achieve (Frobisher et al 2007);
• Specify locations and describe spatial relationships using coordinate geometry and other representational systems (coordinate geometry);
• Apply transformation and use symmetry to analyse mathematical situations (transformational geometry); and
• Use visualisation, spatial reasoning and geometric modelling to solve problems.
Effective instruction in geometry requires teachers to develop sound instructional strategies and knowledge of useful resources and activities (Ding & Jones 2006). Effective mathematics teachers reflect on their connected mathematical knowledge bases and fluidly combine them with their experience and understanding of geometry when teaching (Luneta 2013). These knowledge bases include content knowledge, pedagogical content knowledge (PCK), conceptual knowledge and procedural knowledge. Shulman (1986) regards content knowledge as the main knowledge base that a teacher must possess in order to be effective. Schneider and Stern (2010:178) describe conceptual knowledge as "providing an abstract understanding of the principles and relations between pieces of knowledge in certain domains". Zakaria and Zaini (2009) describe procedural knowledge as a learner's ability to provide mathematical answers without giving reasons why certain steps, methods, operations or formulae were used. Star (2002) and McCormick (1997) explain that procedural fluency is the 'know-how-to-do-it knowledge' of mathematical knowledge, which involves the ability to quickly recall and accurately execute procedures, and according to Danley (2002), it involves engaging in practice with procedures and manipulation of numbers. Content knowledge is knowledge of the subject matter, which, according to Hill, Blunk, Charalambous et al (2008:78), is divided into 'common content knowledge' (CCK), which is commonly held mathematical knowledge that anyone who knows mathematics would possess, and 'specialised content knowledge' (SCK), which is mathematics knowledge specific to the teaching of the subject. As "the experiential knowledge and skills acquired through classroom experience" (Lee & Luft 2008), PCK includes knowledge of how learners learn specific content and the misconceptions and errors associated with certain concepts, as well as of the assessment tasks, remedial activities and enrichment tasks needed to challenge learners. Hill et al (2008) expand PCK to include SCK, which they relate to mathematics knowledge for teaching (MKT), the essential knowledge that good teachers of mathematics ought to possess if they are to be effective.
Figure 2 presents a summary of the mathematics content, specifically the basic geometry content, contained in the National Curriculum Statement (NCS) (RSA DBE 2010). By implication, the figure illustrates the basic common content knowledge of space and shapes that learners who have completed Grade 12 ought to possess by the time they enter university. The summary shows that Grade 12 learners who have successfully passed mathematics should have some basic knowledge, such as knowledge of polygons and polyhedrons and their properties, and should be able to solve problems involving the perimeter and area of 2-D shapes and the volumes of 3-D objects.

The researcher went further and analysed the mathematics curricula on 2-D and 3-D shapes covered in the foundation phase course at university in order to provide a holistic view of the knowledge that foundation phase teachers are envisaged to posses. Thus Figure 2 also shows the knowledge that graduates of foundation phase programmes ought to demonstrate on completion of a teacher education course at university, which should enable them to disseminate content to learners in ways that ensure that they are able to construct their own knowledge of the concepts involved. This would mean enabling learners to acquire and move smoothly through the appropriate levels of geometric thought. Novice teachers should demonstrate effective instructional skills and good assessment techniques. They should identify and remedy learners' misconceptions and enrich them where necessary. Neophyte teachers need to have 'modified' content knowledge and pedagogical content knowledge in order to teach effectively (Hill et al 2008; Rosemary & Feldman 2009; Shulman 1986; Van de Walle 2004).
A descriptive inquiry
Kumar (2011:10) states that a "study classified as a descriptive study attempts to describe systematically a situation, problem, phenomenon or service, or provides information about, say, the living conditions of a community, or describes attitudes towards an issue". In this inquiry, a group of 128 first-year foundation phase teacher education students were tested (see Appendix) on their knowledge of two- and three-dimensional geometric shapes. The items on the test were extracted from a standardised elementary school teachers' test, the 'Mathematics Activities for Elementary School Teachers' (Dolan & Williamson 1990).
Two methods of collecting data from the cohort of 128 foundation phase first-year students were used. The first was a test to collect data that certified the student teachers' knowledge of 2-D and 3-D shapes upon entering university. The second method was focus group interviews that addressed the same content as the test, but which aimed to elicit qualitative responses that could shed light on the test results. In these interviews, students were asked questions similar to those in the questionnaire, but this time they were required, in group conversation, to explain, for instance, the difference between a rhombus and a square or to provide the properties of various polygons and polyhedrons. The expectation was that having successfully completed Grade 12 mathematics, they would be able to talk about their understanding and thus operate at level 3 of Van Hiele's theory, which requires them to "constantly justify their reasoning" (Lim 2006:34).
For the semi-structured group interviews, the researcher divided the participants into twelve groups of ten students, and one for the remaining eight students. The groups were randomly sampled, with each student assigned a number from 1 to 128. The even numbered students formed the first six groups and the other five were made up of odd numbered students. The last group was made up of an equal number of odd and even numbered students. The interviews were conducted over two days and lasted about 30 minutes on average. The students took turns to answer questions and the other members of the group would affirm or refute the answer and discuss it further. The interviews were video recorded and transcribed.
Data analysis
Figure 3 shows an example of an erroneous response to a question on quadrilaterals. The majority of the students (74%) could not define a quadrilateral. The answers they gave, such as the ones in Figure 3, showed that most (69%) could not tell the difference between a triangle and a quadrilateral (basic polygons).

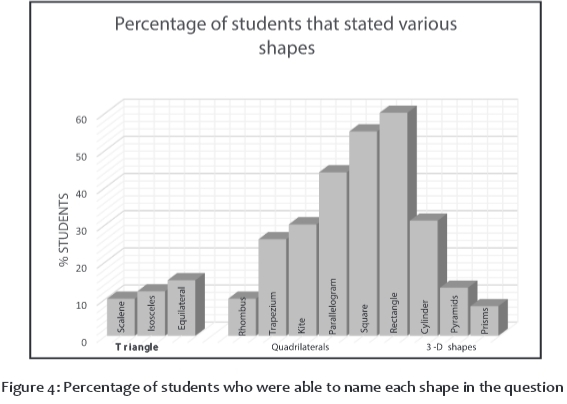
Figure 4 shows the percentages of students who were able to name particular shapes. Only 32 (25%) named all three types of triangles and no student named all the quadrilaterals. The most commonly identified 3-D shape was the cylinder, although it was only identified by 29% of the students. The most frequently identified prism was the cuboid, identified by 32%. Only four students (3%) could name 3-D shapes such as a triangular prism, rectangular pyramid, sphere and other polyhedrons. According to Van Hiele's theory, one can expect children in the first grade to be on the first level, which predicts that they will recognise geometric figures based on their appearance and not their properties. On this level, children are mainly learning the names of shapes, for example a square, triangle, rectangle and circle. As can be seen from Figure 4, this ability was lacking among most (68%) of the first-year foundation phase students. Frobisher et al (2007) assert that it is at the elementary level that learners investigate geometric shapes and are guided to reach the second Van Hiele level (descriptive/analytic), which is where they are able to identify properties of figures, instead of relying on appearance. Figure 4 shows that less than 20% of the foundation phase entrants could be classified as having acquired level 2.
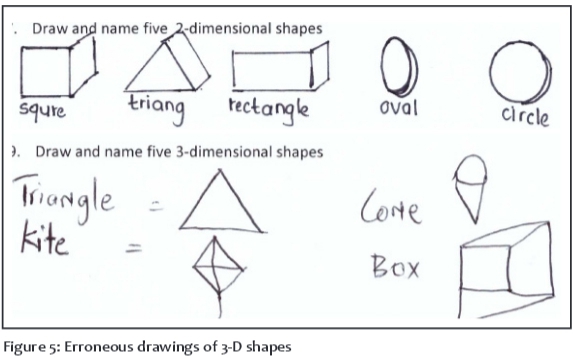
The majority (63%) of students could not tell the difference between 2-D and 3-D shapes, as illustrated by the example of erroneous responses in Figure 5.
Geometry is a branch of mathematics that is beset with various terms learners must know. According to Frobisher et al (2007:27), "accurate, well-defined geometric language is necessary for understanding and talking with others about geometric principles and relationships". Level 3 of the Van Hiele theory requires learners to explain and provide reasons for their results or answers in geometry (Lim 2006).
When asked to define terms such as 'polygon' and 'polyhedron', very few (16%) participants gave the correct answers. Figure 6 shows two of the wrong answers to these questions.

In addition, only 22% of the 128 participants provided correct answers to all the questions on perimeter, area and volume. Figure 7 provides examples of wrong answers to two of these questions.

In South Africa, the NCS (RSA DBE 2010) requires learners to be conversant with basic geometry and operate at levels 2 and 3 of Van Hiele's levels of geometric thought upon exiting high school at the end of Grade 12. Elsewhere, studies (Lim 2006; Wu & Ma 2006) also confirm that learners who successfully complete secondary should be operating at level 3 of Van Hiele's theory. However, the present study established that the majority of the first-year teacher education students operate at level 1. The errors presented in Figures 3, 4, 5, 6 and 7 demonstrate that a significant number (78%) of these foundation phase entrants have deep-rooted misconceptions of basic geometric concepts. The lesson to be learnt here is that programme and curriculum developers at teacher education institutions should ensure that basic geometric concepts, such as basic polygons and polyhedrons, are not only revised but actually taught as if first-year students were encountering them for the first time
Analysis of interviews
Based on Freeman's (1998:90) definition of data analysis as the "process of drawing responses out of the data, or finding them in the data", the study data was analysed inductively, in the sense that there were no predetermined categories or themes, but rather the synthesis of the students' basic knowledge of geometry induced the conclusion (Mertler & Charles 2005). The data was analysed by interpreting the students' responses (Creswell 2012). The questions used in the semi-structured focused group interviews were similar to those in the questionnaire, but required students to explain their answers, and thus to engage in spoken language in 'conversational' mode. For instance, the first question required the whole group to list all the shapes they could recall. The rectangle and square were the first ones to be identified; however, when asked to name the properties of a rectangle and a square, fewer than 10% of the students in the groups mentioned that all the interior angles must be right angles.
When asked if there was any relationship between a square, a rectangle, a rhombus and a parallelogram, they were puzzled to learn that all were parallelograms. Many (72%) could not explain the difference between a square and a rhombus, while 64% did not know what a rhombus was and claimed to be hearing the word for the first time.
The vast majority (94%) of the participants were unable to define a polygon, claiming that they remembered the word but could not define it. They argued about whether triangles and quadrilaterals belonged to the family of polygons, with one student emphatically stating: "It is only the 'gon' family such as pentagon, hexagon and octagon that I think are polygons." Understandably, most (86%) students could not relate to the word 'polyhedron', claiming that they were hearing it for the first time. "I have heard of the word polygon, Sir, but not polyhedron, 'siyezwana'," one student said; he then conferred in the vernacular with his colleagues in the group, who, in chorus, agreed with him.
Although the participants said that they had heard of 3-D shapes, only five students from all eleven groups could tell the difference between a pyramid and a prism, with the majority (96%) admitting that they could draw neither and expressing surprise when told that a cuboid was a prism.
Although many students (88%) from all groups could recall the formula for the area of a rectangle, they could not tell the difference between area and perimeter. Many (74%) could not recall the formula for the volume of a 3-D shape, but when reminded of length x breadth x height there was a resounding "Ooh yes!" When prompted with concepts such as the total surface area of a cuboid or cube, or the volume of a cylinder, cone or a triangular prism, most (78%) of the students admitted that they could not explain these concepts and would not be able to respond to questions pertaining to them in a test.
It was evident from the two data sets (the questionnaire and group interviews) that the participants' knowledge of basic geometry was weak, with most (78%) of them operating at level 1 of Van Hiele's theory of geometric thought (see Lim 2006). From this study one can extrapolate that, despite having passed mathematics in Grade 12, which is a prerequisite for entry to foundation phase teacher education programmes, the majority of students entering such programmes at university have only rudimentary knowledge of basic geometry.
Conclusion: The vexing question of teachers' content knowledge
The objective of the study was to establish the level of basic knowledge of geometry that foundation phase students bring to the programme at university. The study used Van Hiele's theory of geometric thought to gauge students' levels of geometric engagement and revealed that although they had passed Grade 12 mathematics, they were operating at level 1, the level assigned to someone learning geometry for the first time (Lim 2006). The students' knowledge of basic geometry was found wanting, supporting other South African studies which established that, in general, Grade 12 learners have weak knowledge of geometry (Atebe 2008; Feza & Webb 2005). According to Van Hiele's theory (1986), a learner cannot progress to the next level of geometric thought without completing the previous one.
Effective instruction is needed to help learners move through levels, which implies that teachers must be competent and have a basic knowledge of what they are teaching. Although foundation phase students may arguably not need to teach the concepts that were tested and discussed in this study, the evidence of how little they know of basic geometry is disconcerting.
An immediate recommendation resulting from this inquiry is that first-year mathematics curricula for foundation phase teacher students should incorporate basic geometry. The study of geometry, like the other branches of mathematics, begins in early childhood and the formation of the first geometric concepts forms the basis for the rest of geometry. This implies that in order to address the issue of effective geometry instruction at secondary school, one needs to focus on the instructional approaches and content knowledge of primary school teachers.
References
Atebe, H.U. 2008. Students' Van Hiele levels of geometric thought and conception in plane geometry: A collective case study of Nigeria and South Africa. Unpublished PhD thesis. Grahamstown: Rhodes University. [ Links ]
Bahr, K., Bahr, L. & De Garcia, L. 2010. Elementary mathematics is anything but elementary: Content and methods from a developmental perspective. London: Cengage Learning. [ Links ]
Bassarear, T. 2012. Mathematics for Elementary School Teachers. Fifth edition. Belmont, CA: Brooks/Cole. [ Links ]
Battista, M.T. 2007. The development of geometric and spatial thinking. In F. Lester (Ed.), Second Handbook of Research on Mathematics Teaching and Learning. Charlotte, NC: NCTM/Information Age Publishing. 843-908. [ Links ]
Bruner, J.S. 1960. The process of education. Cambridge, MA: Harvard University Press. [ Links ]
Burger, W.F. & Shaughnessy, J.M. 1986. Characterizing the Van Hiele levels of development in geometry. Journal for Research in Mathematics Education, 17(1):31-48. [ Links ]
Chambers, P. 2008. Teaching Mathematics: Developing as reflective secondary teachers. London: Sage Publications. [ Links ]
Clements, D.H. & Sarama, J. 2000. Teaching children mathematics. The National Council of Teachers of Mathematics. Reston, VA: NCTM. [ Links ]
Clements, D.H., Swaminathan, S., Hannibal, M.A.Z. & Sarama, J. 1999. Young children's concepts of shapes. Journal of Research in Mathematics Education, 30(2):192-212. [ Links ]
Cooke, H. 2007. Mathematics for Primary and Early Years: Developing Subject Knowledge. Second edition. London: Sage Publications. [ Links ]
Creswell, J.W. 2012. Educational research: Planning, conducting, and evaluating quantitative and qualitative research. Fourth edition. Milan: Pearson. [ Links ]
Danley, K. 2002. Mathematical Proficiencies. Principal, Starline Elementary School. [ Links ]
Ding, L. & Jones, K. 2006. Teaching geometry in lower secondary school in Shangai, China. Proceedings of the British Society for Research into Learning Mathematics, 26(1):41-46. [ Links ]
Dolan, D. & Williamson, J. 1990. Mathematics Activities for Elementary School Teachers: A Problem-Solving Approach. New York: Addison-Wesley. [ Links ]
Eisenhart, M., Borko, H., Brown, C., Jones, D. & Agard, P. 1993. Conceptual knowledge falls through the cracks: Complexities of learning to teach mathematics for understanding. Journal for Research in Mathematics Education, 24(1):8-40. [ Links ]
Ernest, P. 2010. Reflections on theories of learning. In B. Sriraman & English, L.D. (Eds.), Theories of mathematics education: Seeking new frontiers. London: Springer. [ Links ]
Faulkenberry, E.E.D. 2003. Secondary mathematics pre-service teachers' conception of rational numbers. Unpublished PhD thesis. Stillwater, OK: Oklahoma State University. [ Links ]
Feza, N. & Webb, P. 2005. Assessment standards, Van Hiele levels, and grade seven learners' understandings of geometry. Pythagoras, 62:36-47. [ Links ]
Freeman, D. (Ed.). 1998. Doing Teacher-Research: From inquiry to understanding. Tokyo: Heinle & Heinle Publishers. [ Links ]
Frobisher, L., Frobisher, A., Orton, A. & Orton, J. 2007. Learning to Teach Shapes and Space. Cheltenham: Nelson Thornes. [ Links ]
Fuller, R.A. 1997. Elementary teachers' pedagogical content knowledge of mathematics. Mid-Western Educational Researcher, 10(2):9-16. [ Links ]
Gagne, R.M. 1985. The conditions of learning and the theory of instruction. New York: Holt, Rinehart, Wiston. [ Links ]
Haapasalo, L. & Kadijevich, D. 2000. Two types of mathematics knowledge and their relations. Journal für Mathematik-Didaktik, 21(2):139-157. [ Links ]
Hiebert, J. & Carpenter, T. 1992. Learning and teaching with understanding. In D. Grouws (Ed.), Handbook of Research on Mathematics Research and Teaching. New York: MacMillan. 65-100. [ Links ]
Hill, H.C., Blunk, M.L., Charalambous, C.Y., Lewis J.C., Phelps, G.C., Sleep, L. & Ball, D.L. 2008. Mathematical knowledge for teaching and the mathematical quality of instruction: An exploratory study. Cognitive and Instruction, 26:430-511. [ Links ]
Kilpatrick, J., Swafford, J. & Findell, B. (Eds.). 2001. Adding it up: Helping children learn mathematics. Washington, DC: National Academy Press. [ Links ]
Kumar, R. 2011. Research Methodology: A step-by-step guide for beginners. Third edition. London: SAGE. [ Links ]
Lee, E. & Luft, F.A. 2008. Experienced secondary school teachers' representation of pedagogical content knowledge. International Journal of Science Education, 30(10):1343-1363. [ Links ]
Lim, S.K. 2006. Applying the Van Hiele theory to the teaching of secondary school geometry. Teaching and Learning, 13(1):32-40. [ Links ]
Luneta, K. 2013. Teaching elementary mathematics: Learning to teach elementary mathematics through mentorship and professional development. Saarbrücken: LAP LAMBERT Academic Publishing GmbH & Co KG. [ Links ]
Maree, K. (Ed.). 2011. First steps in research. Seventh impression. Pretoria: Van Schaik Publications. [ Links ]
Mayberry, J.W. 1983. The Van Hiele levels of geometric thought in undergraduate pre- service teachers. Journal for Research in Mathematics Education, 14(1):58-69. [ Links ]
McCormick, R. 1997. Conceptual and procedural knowledge. International Journal of Technology and Design Education, 7:141-159. [ Links ]
McGehee, J.J. 1990. Prospective secondary teachers' knowledge of the function concept. Unpublished PhD thesis. Austin, TX: University of Texas. [ Links ]
Merriam, S.B. 2009. Qualitative Research: A guide to design and implementation. Revised and Expanded from Qualitative Research and Case Study Applications in Education. San Francisco, CA: Jossey-Bass. [ Links ]
Mertler, C.A. & Charles, C.M. 2005. Introduction to Educational Research. Fifth edition. Munich: Pearson. [ Links ]
Musser, L.G., Burger, W.F. & Peterson, B.E. 2011. Mathematics for Elementary Teachers: A Contemporary Approach. Ninth edition. Wiley.
NCTM (National Council of Teachers of Mathematics). 2000. Curriculum and Evaluation Standards for School Mathematics. Reston, VA: NCTM. [ Links ]
Piaget, J. 1952. The origin of intelligence in children. New York: W.W. Norton. [ Links ]
Pusey, E.L. 2003. The Van Hiele model of reasoning in geometry: A literature review. Unpublished MSc thesis. Raleigh, NC: North Carolina State University. [ Links ]
Rittle-Johnson, B. & Alibali, M.W. 1999. Conceptual and procedural knowledge of mathematics: Does one lead to the other? Journal of Educational Psychology, 9(1):175-189. [ Links ]
Rittle-Johnson, B. & Siegler, R.S. 1998. The relation between conceptual and procedural knowledge in learning mathematics: A review. In C. Donlan (Ed.), The development of mathematical skills London: Psychology Press. 75-110.
Rosemary, C.A. & Feldman, N. 2009. Professional development settings: More than time, place, activity. Retrieved from http://www.literacycoachingonline.org/briefs.html (2 February 2012).
RSA DBE (Republic of South Africa. Department of Basic Education) 2010. National Curriculum Statement for Grades R-9. Pretoria: DBE. [ Links ]
RSA DoE (Republic of South Africa. Department of Education). 2006. The National Policy Framework For Teacher Education and Development in South Africa. "More teachers; Better teachers". Pretoria: DoE. [ Links ]
Schneider, M. & Stern, E. 2010. The developmental relations between conceptual and procedural knowledge: A multimethod approach. Developmental Psychology, 46(1):178-192. [ Links ]
Shulman, L.S. 1986. Those who understand knowledge growth in teaching. Educational Researcher, 15(2):4-14. [ Links ]
Skemp, R.R. 1971. The psychology of learning mathematics. Baltimore, MD: Penguin Books. [ Links ]
Star, J.R. 2002. Developing conceptual understanding and procedural skill in mathematics: An interactive process. Journal of Educational Psychology, 93(2):346-362. [ Links ]
Van de Walle, J.A. 2004. Elementary school mathematics: Teaching developmentally. Fourth edition. New York: Longman. [ Links ]
Van Hiele, P.M. 1986. Structure and insight: A theory of mathematics education. Orlando, FL: Academic Press. [ Links ]
Van Hiele, P.M. 1999. Developing geometric thinking through activities that begin with play. Teaching Children Mathematics, 5:310-316. [ Links ]
Van de Sandt, S. 2007. Pre-service geometry education in South Africa: A topical case? IUMPST: The Journal (Content Knowledge), 1:1-9. [ Links ]
Vygotsky, L.S. 1978. Mind in society: The development of higher psychological processes. Cambridge, MA: Harvard University Press. [ Links ]
Wu, D. & Ma, H. 2006. The distribution of Van Hiele levels of geometrical thinking among 1st through 6th graders. In J. Novotná, H. Moraová, M. Krátká & N. Stehlíková (Eds.), Proceedings of the 30th Conference of the International Group for the Psychology of Mathematics Education. Prague: PME. 409-416. [ Links ]
Zakaria, E. & Zaini, N. 2009. Conceptual and procedural knowledge of rational numbers in trainee teachers. European Journal of Social Sciences, 9(2):202-217. [ Links ]
* Email address: kluneta@uj.ac.za
APPENDIX
Diagnostic test on space and shape for foundation phase student teachers as they enter university
NAME: .....................................................................................................
STUDENT NUMBER: ....................................................................................
NOTE: Attempt all the questions to the best of your ability. Use the space provided under each question. The results will be used for research purpose only and will have no bearing on your studies at the university or elsewhere.
1. What is a shape?
2. Name as many shapes as you can remember.
3. What is a quadrilateral?
4. Draw five quadrilaterals.What is a polygon?
5. Draw and name five polygons.
6. Draw and name five two-dimensional shapes.
7. What is a polyhedron?
8. Draw and name five three-dimensional shapes.
END OF TEST AND THANK YOU FOR PARTICIPATING IN THE STUDY














