Services on Demand
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
South African Journal of Childhood Education
On-line version ISSN 2223-7682
Print version ISSN 2223-7674
SAJCE vol.11 n.1 Johannesburg 2021
http://dx.doi.org/10.4102/sajce.v11i1.871
ORIGINAL RESEARCH
Mapping pre-service teachers' faulty reasoning in geometric translations to the design of Van Hiele phase-based instruction
Nokwanda P. MbusiI; Kakoma LunetaII
ISchool of Early Childhood Development, Faculty of Education, University of Mpumalanga, Siyabuswa, South Africa
IIDepartment of Childhood Education, Faculty of Education, University of Johannesburg, Johannesburg, South Africa
ABSTRACT
BACKGROUND: Pre-service teachers (PSTs) training does not equip students with adequate skills and knowledge of geometry to enable them to teach this section of mathematics competently. Inadequate teacher knowledge of transformation geometry, in particular, requires intervention that targets PSTs' faulty reasoning displayed in errors they make.
AIM: The aim of this study was to explore the use of Bachelor of Education (BEd) students' faulty reasoning in geometric translations, in designing a Van Hiele phase-based instructional programme that could address such faulty reasoning.
SETTING: The setting for the study was a newly established rural university in South Africa.
METHODS: Tests on geometric translations were administered to BEd Foundation Phase students, followed up by interviews to explore errors made when responding to the test items. The errors were then mapped to the design of a Van Hiele phase-based instructional programme.
RESULTS: The results revealed that the students had several misconceptions with geometric translations. The misconceptions were delineated into the errors that the students displayed and these were classified under two themes. The first theme was incorrect properties of transformation and under this theme, the errors were coded as confusing translation with rotation, wrong translation method, incorrect interpretation of coordinates and confusing the x and y axis. The second theme was errors involving basic mathematics operations including wrong diagrammatic representation of coordinates and incorrect calculations.
CONCLUSION: The study showed that if the students' misconceptions and the resulting errors are mapped to specific instructional approaches, their faulty reasoning in geometric transformations is addressed and effective learning is enhanced.
Keywords: errors and misconceptions; Van Hiele theory; instructional design; geometric translations; intervention.
Introduction
Low performance in mathematics has been a worldwide challenge for many decades, for instance, in 1989, the then president of the International Commission on Mathematics Instruction (ICMI), Dr Hassler Whitney said 'for several decades we have been seeing increasing failure in school mathematics education, in spite of intensive efforts in many directions to improve matters'. This scenario is true even today. Mathematics education in South Africa is labelled as being in a state of crisis, with learners performing dismally in several international assessments such as Trends in International Mathematics and Science Studies (TIMSS) (Spaull 2013). Further evidence attests to the fact that learners' poor performance in mathematics is, to some extent, associated with the kind of teaching and learning that students obtain throughout their schooling years. For example, Stols et al. (2015) raised the concern that mathematics education offered to South African learners remains inferior, even though it has been acknowledged as one of the country's national priorities. Inadequate or deficient teaching of mathematics is more pronounced within the geometry section. For instance, research has shown that geometry receives little attention in both primary and high school teaching as teachers focus mainly on arithmetic or algebra (Makgato & Mji 2006; Sinclair & Bruce 2015). Hence, student performance in geometry has contributed significantly to the overall low performance in mathematics over the years (Evbuomwam 2013).
Teachers are believed to play a significant role in the quality of mathematics that is offered to students, through the knowledge that they bring to the classroom (Ball, Hill & Bass 2005; eds. Rowland & Ruthven 2011). Therefore, efforts to improve students' performance in mathematics need to involve the empowerment of teachers with better knowledge and skills that enable them to teach mathematics effectively. This is crucial, especially given the inadequacy of teacher training in preparing teachers for teaching mathematics effectively. Teachers' lack of requisite mathematical knowledge and skills disadvantages students, who, most of the time, depend on teachers for their achievement in mathematics (Graven, Hewana & Stott 2013). Besides teachers' lack of adequate general knowledge of mathematics for teaching, research also shows that the situation is dire when it comes to their knowledge of geometry (Ndlovu 2012), especially with teachers at primary education level (Luneta 2014; Žilková, Gunčaga & Kopáčová 2015). Hence, studies that focus on the improvement of primary school pre-service teacher's (PST's) knowledge and understanding of geometry are desirable. A significant part of improving that knowledge would be to understand the challenges PSTs encounter when studying and teaching geometry and address them.
This article is derived from a bigger study that sought to examine PSTs' challenges with transformation geometry in the context of primary school teacher training. The focus here is on exploring problems involving geometric translations, in order to design relevant instructional activities that will address such challenges. Through the researchers' experience of teaching transformation geometry to students in the Bachelor of Education (BEd) in Foundation Phase (FP) programme, they have seen the errors displayed and misconceptions held by students when learning about this topic. This study therefore seeks to explore these errors and map them to the design of a programme of instruction that is informed by Van Hiele phase-based learning. The error mapping intervention was intended to assist the researchers and other mathematics lecturers and teachers in general in mediating the teaching of geometric translations.
Research indicates that even though teachers are able to identify overall trends and weaknesses in their learners' work, they lack skills to apply this knowledge in developing a suitable intervention programme (Holmes et al. 2013). Furthermore, intervention programmes that mitigate against student's poor performance in mathematics in the South African context, often focus on high school level, despite evidence that achievement is best raised by focusing on the primary school level (ed. Bernstein 2013). This study therefore contributes towards focusing intervention towards the required mathematics content and level: the improvement of geometry teaching and learning at the FP level of PST training.
Problems experienced by students with geometry in general and transformation geometry in particular
Deficiencies in geometric reasoning exist with both students and teachers. Studies involving investigations into South African pre-service mathematics teachers' levels of reasoning in geometry revealed that many teachers struggle to solve geometric problems that require logical abstract reasoning in the proof of statements made (Van Putten 2008). The findings of another study conducted by Adolphus (2011) in Nigeria concluded that most mathematics teachers have a poor foundation in geometry and are therefore not capable of teaching geometry well. Moss et al. (2015) supported the assertion that teachers, especially at the primary school level, have inadequate knowledge of geometry, resulting in geometry not receiving adequate teaching time.
Transformation geometry deals with the way geometrical shapes or objects are changed into their various images under a transformation. Transformation geometry covers translations (all points of the shape are moved through the same distance in the same direction on a plane), reflections (a line is used like a mirror to reflect a figure) and rotations (a shape is turned about a point through a given angle) (Aktaş & Ünlü 2017; Bansilal & Naidoo 2012; Evbuomwan 2013). Transformation geometry has been identified as one aspect of geometry where students experience challenges (Ada & Kurtulus 2010; Bansilal & Naidoo 2012; Evbuomwan 2013; Luneta 2015b). For example, students lack understanding of the geometric meaning of translations and rotations, even though they seemed capable of working with algebraic calculations involving these types of transformations (Ada & Kurtulus 2010). On the contrary, in Naidoo & Bansilal's (2010) study, students did not work competently with algebraic problems because of confusing rules of transformation geometry such as the rules of reflection with those of rotation. A study by Luneta (2015b), which focused on Grade 12 students' knowledge of geometry, outlines some of the problems students encounter when solving tasks or involving transformation geometry. Amongst the errors students exhibited were confusing the line y = x with the y- and x-axis.
Foundation Phase student teachers, in particular, tend to have limited basic knowledge of transformation geometry, which leads to the confusion of the properties of, and applicable rules between the different types of transformations (Luneta 2014). This confirms earlier studies by Gomes (2011), who discovered that even though elementary teachers seemed aware of some of the properties such as the preservation of length, orientation and parallelism, they could not correctly perform a horizontal translation of a horizontal flag. A study by Kurt-Birel, Deniz and Önel (2020) further alluded to primary school teachers' weak knowledge of properties of transformation geometry (translation, reflection and rotation). They concluded that most prospective primary school teachers' knowledge of translation was fragile and they exhibited difficulty in explaining and understanding concept involved, such as defining translation whilst relating it with a plane, motion, transformation or vector. Bansilal and Naidoo (2012) also highlighted the lack of visualisation skills with teachers and the subsequent inability of teachers to use visualisation as a reasoning process and tool. Visualisation skills are a significant part of learning transformation geometry because physical changes between an object and the image involve visual differences that need to be discerned (Mudaly & Rampersad 2013).
Students' misconceptions and the associated errors in transformation geometry are stubborn and persistent (Bansilal & Naidoo 2012). Further studies and invention initiatives are, therefore, necessary. This research attempted to provide further insights into the notion of effective mathematics teaching approaches by using an intervention strategy. The intervention was a design of an instructional programme that isolated student teachers' errors and mapped them onto a step-by-step procedure aligned to specific activities.
Error analysis
This study involves PSTs' faulty reasoning in transformation geometry. Faulty reasoning is detected in the errors students display. Luneta and Makonye (2010) described an error as a mistake, slip, blunder or inaccuracy and a deviation from accuracy. Errors are often displayed in students' written work or in oral communication. It is from the displayed errors that teachers can associate the underlying misconceptions responsible for them. Hence, misconceptions are not easily detected by simple observation. Hansen (2017) assets that misconceptions might relate to misapplication of certain rules, an over-generalisation or under-generalisation, as well as an alternative understanding of a certain concept. In other reviews, the link between errors and misconceptions is that errors are slip-ups and non-systematic, whilst misconceptions are regarded as the more serious systematic errors (Makonye 2011). Fundamentally, errors are as a result of misconceptions and are formed in a learner's head and displayed on a piece of paper or in a conversation.
Examples of instances that might involve non-systematic errors include the misreading of information by students or unintentionally leaving out an important piece of information. In such cases, students are likely to correct the error themselves, because there is no existence of underlying faulty conceptual understanding associated with the error. On the other hand, systematic errors involve the lack of understanding of underlying concepts (Makonye 2011). In such cases, the teacher often needs to guide the student towards identifying and correcting the error.
Analysis of errors was critical in this study because as the preceding literature indicates that students' challenges with transformation geometry were because of some underlying misconceptions that resulted in errors. Hence, such misconceptions need to be explored, if intervention efforts are to be successful. The importance of analysing students' errors lies in the benefit that they derive from being made aware that, for example, the conception they have been holding onto has been arrived at by flawed methods, which then impedes their performance in the subject (Schepper & McCoy 2013). However, the intention is not to make students feel guilty for making errors. Instead, they should consider errors as bouncing boards for conceptual knowledge acquisition and form an important part of the learning process (Hansen 2017). Matteucci, Corazzal and Santagata (2014) concurred that student errors cannot be avoided. Instead, teachers should use the existence of errors to redesign lessons by making errors catalysts for learning (Bray & Santagata 2014).
The misconception and the errors that result in students' incorrect or faulty reasoning have to be isolated and unpacked, so that attempts at intervention target the correct concept or procedures needed to address them. One way of unpacking the errors is by designing learning experiences that are likely to provoke the errors concerned, so that the hidden misconceptions are revealed and corrected (Zehetmeier et al. 2015). Therefore, students must be engaged in conceptual experiences through assessment tasks and other learning activities to allow the misconceptions to emerge. Such engagements provide teachers with opportunities to revise or adjust their teaching approach (Shalem, Sapire & Sorto 2014). The intervention programme that resulted from this study served the purpose of facilitating prolonged engagement with PSTs and points to various strategies that addressed misconceptions and resulting errors that were because of the lack of conceptual understanding of transformation geometry.
The use of error analysis to design a comprehensive instructional programme that uses students' errors and faulty reasoning in transformation geometry as a starting point is one of the strengths of this study. This, especially, in the absence of error analysis acts as a tool to diagnose and address learner challenges in transformation geometry in the context of South African PST education programmes (Luneta 2008). It is further envisaged that this study would benefit lecturers in teacher education and teachers of mathematics in general. PSTs and teachers can use the study and the instructions programme developed to enhance the learning and teaching of transformation geometry. Alternatively, teachers can adapt the programme and use it towards developing their own instructional programmes based on analysis of student errors. Riccomini (2005) declared that whilst teachers might succeed in describing and understanding errors made by their students, most of them still lack the skills needed to align their lessons with the errors identified.
Van Hiele theory
A Dutch couple, Pierre van Hiele and Dina van Hiele, in their work as mathematics teachers, conducted extensive research with the aim of understanding students' reasoning in geometry. The results of their research culminated in the formulation of the now seminal Van Hiele theory, which is premised on the idea that students go through five levels of reasoning when working with geometric concepts: Recognition or visualisation, Analysis or Descriptive, Ordering or Informal deduction, Formal deduction and Rigour (Pusey 2003; Van Hiele 1986).
The strength of Van Hiele levels lies in the role of the teacher during the teaching and learning situation, where the student is guided using language that is appropriate for a specific level, towards achieving the next, higher level of reasoning.
In an attempt to help students proceed from one level to the next, the Van Hiele theory proposes five phases of learning that teachers can use to plan instruction (Abdullah & Zakaria 2013; Alex & Mammen 2016; Crowley 1987; Pusey 2003):
-
Information phase - The teacher determines students' prior knowledge, which helps in deciding how to pitch the introductory activities for the topic of interest.
-
Guided Orientation phase - Students are guided by the teacher, using simple but carefully structured tasks, towards making discoveries about the topic and helping them progress from one level to the next.
-
Explicitation phase - The teacher assesses students' progress by asking them to explain their understanding about the topic, in their own words, and then introduces formal vocabulary where students used non-technical terms.
-
Free Orientation phase - Students work on open-ended and more challenging activities, including investigations to discover relationships between concepts. They are expected to use the correct vocabulary which has been developed in previous phases.
-
Integration phase - The teacher asks students to review and summarise the subject matter they have learned, in order to determine if they have developed an overall understanding of the topic of interest.
The Van Hiele theory proved to be a valuable framework in various studies that used it to explore and address students' problems with geometry (Panaoura & Gagatsis 2009, Bansilal & Naidoo 2012, Luneta 2015b, Alex & Mammen 2016). A common outcome that is realised using Van Hiele theory is that, for instruction to be effective, the communication between the teacher and the students has to be at the level of development of the students. Teachers need to use a language that matches the reasoning capabilities of the students, and then gradually guide them towards using the correct mathematical vocabulary by the end of the lesson. Failure to do this could result in the teachers' intended communication being interpreted incorrectly (Kuzniak & Rauscher 2011), which could lead to a lack of conceptual understanding and the development of misconceptions (Mateya 2008). Continuous and focused engagement with students, using a carefully planned instructional programme has a potential to enable the teacher to pick up possible miscommunication and address it.
Most studies applied Van Hiele theory at the schooling level than at the post-school level. Hence, Feza and Webb (2005) suggested more application of the theory in pre-service and in-service mathematics teacher training. This study therefore has the potential to contribute to knowledge in this field. Some teachers registered their difficulty in implementing effectively a geometry curriculum which they did not design themselves (Yilmaz et al. 2011). If such teachers could start by identifying their own students' faulty reasoning in geometric concepts and contribute towards the design of the instructional programmes, such as the one in the current study, there is a possibility of an increase in competence and confidence amongst teachers. The added benefit of such contextualised contributions could be the reduction of dependency on textbooks, which is either not easily available (Ilaslan 2013), or provides simplistic and routine-like approaches to the teaching of mathematical concepts (Luneta 2015a).
Despite its significant contribution to the teaching and learning of geometry, the Van Hiele theory has been questioned for some of its potential weaknesses (Sinclair & Bruce 2015). For example, concerns have been raised that there is a possibility of students being in transition between levels or advancing to higher levels with some concepts and not with other (Mayberry 1983). This study took cognisance of these important observations by ensuring that the interventions at various levels of the Van Hiele theory were comprehensive and included various assessment tasks and illustrations and the teaching approach was research-based (Pegg 1985).
Based on its success in analysing student reasoning with geometry, as well as its potential in addressing challenges that students might have with understanding transformation geometry, the Van Hiele theory is used in this study to achieve the objective as articulated below.
The objective of this study was to explore BEd in FP students' faulty reasoning in geometric translations in order to design a Van Hiele phase-based instructional programme.
Therefore, the study sought to answer the following main research question:
How can BEd FP students' faulty reasoning in geometric translations be used to design a Van Hiele phase-based instructional programme:
-
What errors and associated misconceptions do BEd (FP) students make and have when solving problems involving geometric translations?
-
What steps can be followed to map student errors and misconceptions in geometric translations to the design of a Van Hiele phase-based instructional programme that can address such faulty reasoning?
Research methods and design
Study design
This qualitative interpretive study (Cohen, Manion & Morrison 2010) sought to gain an in-depth understanding of students' reasoning when working with geometric translations. This understanding would then inform the design of an instructional programme that addressed faulty reasoning amongst students. Therefore, the research approach adopted in this study was design-based research, a formative approach in which a product or process is designed and developed (Swan 2014), with the aim of educational improvement of learning, using a local instruction theory (Gravemeijer & Eerde 2009) of Van Hiele phase-based instruction.
Setting and sampling strategy
The participants for the study were BEd in FP students in their second year of study at a newly established rural university in South Africa. Just under half of the students did Mathematical Literacy (ML) in their matric and the rest, except for one, did Mathematics. This distinction according to the two subjects could have had an effect on student performance because quite a number of students who did ML voiced their concern over the fact that they never did transformation geometry during their Further Education and Training years.
Even though all second year students registered for the mathematics module in the BEd programme formed the target sample and gave consent to participate in the study, 82 students participated in all the phases of data collection. Sampling was purposeful (Creswell 2012). All the students were sampled because, firstly, that was the year in which the topic of transformation geometry was taught and secondly, an intervention programme that was planned for later on had to include these students.
Data collection
Data collection for the study occurred in three stages: tests, interviews and instructional design activities.
Stage 1: Tests
The participants wrote two tests, a short multiple choice (MC) test and a longer discussion (D) test where students had to give explanations or show calculations for their answers. Both tests were administered during the first semester of the year, which coincided with the period during which transformation geometry was supposed to be taught as part of the BEd curriculum. The tests were written before teaching any topic and therefore served as diagnostic tools to assess students' understanding of challenges with geometric translations, so as to answer the first research question (Flick 2018). The test items were adapted from Soon's (1989) Van Hiele like levels for learning transformation geometry (shown in Table 1 for levels 1-4, in the context of this study), Burger and Shaughnessy's (1986) isometric transformations in the Van Hiele framework, as well as Guven's (2012) 'Transformation Geometry Achievement Test' (TGAT) and the 'Learning Levels of Transformation Geometry Test' (LLTGT). This ensured validity and reliability of the MC and the D tests because they were based on the above-mentioned frameworks which have been tested and validated before.
Stage 2: Interviews
Semi-structured interviews were carried out with 21 students as key informants (Cohen, Manion & Morrison 2000) in order to get insight into their faulty reasoning that led to the display of errors. Willing interviewees were selected based on their performance in the tests, in such a way that a wide representation of the test items was included. Student's responses were recorded for accuracy when transcribing and analysing, as well as to capture non-verbal actions or behaviours. The interviews supported data from the tests, in assisting the researchers to understand the misconceptions associated with the errors displayed, and to be able to fully answer the first research question. The use of interviews thus facilitated methodological triangulation (Cope 2014), reduced chances of researcher bias because of possible misinterpretation of errors displayed in test scripts, resulting in increased credibility of the study.
Stage 3: Instructional design activities
Following the analysis of data from the tests and interviews, an instructional design programme, based on Van Hiele phases of learning, was developed. Errors on geometric translations, which were already coded and categorised, were used to develop activities at the different Van Hiele levels. The activities were then linked to the five Van Hiele phases of learning.
Data analysis
Thematic analysis (Braun & Clarke 2006) was used to analyse the tests and the interviews. Students' responses, as recorded in test scripts, were analysed according to Braun and Clarke's (2006) six phases of thematic analysis. That is, the researchers first familiarised themselves with the data, then they generated initial codes, organised the codes into possible themes, reviewed, defined and named the themes to produce the final report. Analysis of interviews started with students' verbal recordings from the video transcripts. A similar process of thematic analysis was used in analysing the tests. The analysis was inductive because the themes were data driven (Clarke & Braun 2014). The themes created from the analysis of tests and interviews were used to answer the first research question. Analysis of data from the Van Hiele phase-based instructional design entailed content analysis of the activities that appeared in each of the phases, at a more micro level (Wilkinson 2000) to see if they were mapped to the correct theme (which represented some type of error). The analysis resulted in a record of clear, step-by-step teaching approaches derived from the analysed errors. The error analysis further gave guidance on how learning can be facilitated using various assessment tasks on transformation geometry.
Ethical considerations
Permission to conduct research was sought and obtained from the University of Johannesburg where the participants were enrolled. Written consent was obtained from all participants in the study, before the commencement of the research activities. The participants were informed of the purpose of the study, the procedures to be followed during the period of participation, such as video recording if they gave consent, as well as the freedom to withdraw from participating in the study any time if they chose to. The participants were further informed of confidentiality regarding sharing information that they might come across during the research, such as their names and their identities. Ethical clearance number: 2018-081
Results
Research sub-question 1
The first research question for the study was: What errors and associated misconceptions do BEd (FP) students make and have when solving problems involving geometric translations?
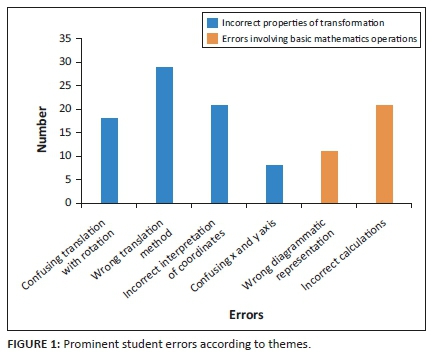
After completing Braun & Clarke's (2006) six phases of thematic analysis, Table 2 was created, depicting the overall themes generated from the analysis of data from tests and interviews in response to the first research question. In response to the question students displayed different forms of errors. Figure 1 shows how thematic analysis was used to formulate themes, which fell under two main categories: non-systematic errors and systematic errors. The figure further illustrates two themes of the most prominent errors, where n represents the number of students that displayed the errors out of 82. The first theme was incorrect properties of transformation and under this theme the errors were coded as: confusing translation with rotation (n = 18); wrong translation method (n = 29), incorrect interpretation of coordinates (n = 21) and confusing the x and y axis (n = 8). The second theme was errors involving basic mathematics operations and under this theme the errors were coded as: wrong diagrammatic representations or interpretations of coordinates (n = 11) and incorrect calculations (n = 21).
Further analysis of the tests and interviews provided the answer to the above question. The first and second columns indicate the number of the question from the original test and an example of a students' faulty response to the question, respectively. Additional researchers' comments or explanations, where applicable, appear in the second column, in bold. The third column indicates, where applicable, key phrases and sentences used by students during interviews to substantiate their (faulty) responses as given in the second column.
The last two columns in the table answer the research question. That is, the errors and associated misconceptions are listed under the two main categories: Non-systematic errors and systematic errors.
Research sub-question 2
The second research question for the study was: What steps can be followed to map student errors and misconceptions in geometric translations to the design of a Van Hiele phase-based instructional programme that can address faulty reasoning?
The programme overview is summarised to indicate how the activities that form part of the programme design were linked to the different Van Hiele phases as well as Van Hiele levels.
Summary of the overview of the program design
The Van Hiele programme design was summarised as depicted in Table 4 and this was used in developing the instructional as well as assessment activities for students.
The starting point towards answering this question was the isolation of the errors, as they appear under each theme from the results of tests and interviews, in Table 3. For each error, an activity that targeted the particular error was then developed and mapped to the error. Each activity had to be aligned to both Soon's (1989) Van Hiele-like levels (in Table 1) as well as to Van Hiele phases of learning. For example, in Table 5, the first four errors and misconceptions on the left-hand column were mapped to the first activity that is described on the right-hand column. This activity is linked to Soon's level 2 characteristic: 'Relates transformations using coordinates'. At the same time, the activity would be used during Van Hiele's Guided Orientation Phase, which has been described in an earlier section under 'Van Hiele theory'. Similar steps were taken to create the other examples of activities that appear in Table 5. Further explanatory notes that accompany each activity have been included in column 2 of the Table in order to justify how each activity is mapped to the error.
Discussion
The main purpose of this study was to explore BEd in FP PSTs' faulty reasoning in transformation geometry, with a focus on geometric translations. The understanding of these faulty reasoning, as displayed through errors made by students, was to be used to design Van Hiele phase-based instructional activities that were mapped to the errors and misconceptions identified. The instructional design was meant to assist teachers and PST educators with the development of instructional material used to facilitate an intervention that would seek to address and help improve students' faulty reasoning in transformation geometry. The instructional design was critical considering the lack of such interventions at the South African primary school level of mathematics education, as well as the scarcity of relevant textbooks for targeted intervention. The mapping of activities to errors formed the major part of the study and the results were a programme that can be replicated with other aspects of transformation geometry such as reflection and rotation.
The results of the study revealed that BEd in FP students have several misconceptions associated with learning and solving tasks involving geometric translations. These errors were classified under two main categories: non-systematic errors and systematic errors, confirming previous studies (Makonye & Luneta 2010). Amongst non-systematic errors, the issue of language deficiencies featured prominently, where students could not effectively communicate their ideas, leading to, for example, incorrect descriptions of geometric translations. This confirms the findings reported in previous studies, especially those that used the Van Hiele theory to explore students' reasoning in geometry in general, and in transformation geometry in particular (Kuzniak & Rauscher 2011). Students also tended to confuse properties of translations with those of other types of transformations. Similar findings were reported in Kaplan and Öztürk's (2014) study, where students struggled to differentiate between properties of figures after translation and reflection. A number of students in the study also made errors involving algebraic calculations, similarly to those of a study by Naidoo and Bansilal (2010), who concluded that students did not work competently with algebraic problems when doing transformation geometry.
The use of Van Hiele phase-based instructional design in this study provides a novel way of using students' errors and misconceptions to enhance learning outcomes. Student errors were mapped successfully to activities designed using both Van Hiele levels and Van Hiele phase-based activities. Step-by step guidance is provided for teachers and other potential beneficiaries in mathematics education on how to map student errors with activities.
We propose for other studies that could work with teachers and PST educators to actually implement an intervention based on Van Hiele phase-based instructional design. Such research could use the activities developed in this study. However, the strength of such implementation would lie in their ability to be innovative as well as to envision how their students might participate in the proposed activities (Gravemeijer & Van Eerde 2009). As shown in the activities designed in this study, the instructional designer must anticipate how students might respond to questions found in the activities, and already have suggestions and alternatives in place for those students who might need remedial support. This is especially important because of the possibility of students who might not conform to the norm of Van Hiele levels, and perhaps be in transition between levels (Sinclair & Bruce 2015).
Conclusion
In this research, a series of activities, based on the Van Hiele phases of learning, were developed, and used during the implementation of an intervention programme to address students' errors in transformation geometry. These activities were organised into a comprehensive document that provides guidelines and activities on teaching transformation geometry to student teachers in the FP. This research thus contributes to knowledge creation. This is important because it gives teachers an idea of how to design and use instructional programmes such as one based on Van Hiele theory to improve learners' reasoning and understanding of geometry, a component of mathematics that presents with challenges throughout the schooling years.
Teacher educators should re-think the strategies they use to address challenges they experience with their students' competence and reasoning in geometry. This study has shown that if student errors and misconceptions are the starting point of lesson planning and design, there are better chances of focusing instruction where it will make an impact, given that one would already know what concepts to target, what concepts to spend more on or be more innovative with. We further point that one should not start from scratch because there are available theories, such as Van Hiele phase-based instruction, that have been well researched and give clear guidelines on how to adapt and use them for one's unique situation.
Acknowledgements
The authors would like to acknowledge the participation of the students from the university where the research was conducted.
Competing interests
The authors have declared that no competing interests exist.
Authors' contributions
N.P.S. collected and analysed data. Both authors contributed equally towards writing this article.
Funding information
This research received no specific grant from any funding agency in the public, commercial or not-for-profit sectors.
Data availability
The data that support the findings of this study are available from the corresponding author, N.P.S., upon reasonable request.
Disclaimer
The views and opinions expressed in this article are those of the authors and do not necessarily reflect the official policy or position of any affiliated agency of the authors.
References
Abdullah, A.H. & Zakaria, E. (2013). 'The activities based on van Hiele's phase-based learning: Preservice teachers' views', Journal of Mathematics and Statistics 8(3), 385-395. [ Links ]
Ada, T. & Kurtulus, A., 2010, 'Students' misconceptions and errors in transformation geometry', International Journal of Mathematical Education in Science and Technology 41(7), 901-909. https://doi.org/10.1080/0020739X.2010.486451 [ Links ]
Adolphus, T., 2011, 'Problems of teaching and learning of geometry in secondary schools in Rivers State, Nigeria', International Journal of Emergent Science 1(2), 143-152. [ Links ]
Aktaş, G.S. & Ünlü, M., 2017, 'Understanding of eight grade students about transformation geometry: Perspectives on students' mistakes', Journal of Education and Training Studies 5(5), 103-119. [ Links ]
Alex, J.K. & Mammen, K.J., 2016, 'Lessons learnt from employing Van Hiele theory based instruction in senior secondary school geometry classrooms', Eurasia Journal of Mathematics, Science & Technology Education 12(8), 2223-2236. https://doi.org/10.12973/eurasia.2016.1228a [ Links ]
Ball, D., Hill, H. & Bass, H., 2005, 'Knowing mathematics for teaching: Who knows mathematics well enough to teach third grade, and how can we decide', American Educator 29(1), 14-17, 20-22, 43-46. [ Links ]
Bansilal, S. & Naidoo, J., 2012, 'Learners engaging with transformation geometry', South African Journal of Education 32(1), 26-39. https://doi.org/10.15700/saje.v32n1a452 [ Links ]
Bernstein, A. (ed.), 2013, Mathematics outcomes in South African schools: What are the facts? What should be done?, Report published by The Centre for Development and Enterprise.
Braun, V. & Clarke, V., 2006, 'Using thematic analysis in psychology', Qualitative Research in Psychology 3(2), 77-101. [ Links ]
Bray, W. & Santagata, R., 2014, 'Making mathematical errors springboards for learning', in Annual Perspectives in Mathematics Edtion (APME): Using Research to Improve Instruction, National Council of Teachers of Mathematics, Reston, VA.
Burger, W.F. & Shaughnessy, J.M., 1986, 'Characterising the van Hiele levels of development in geometry', Journal for Research in Mathematics Education 17(1), 31-48. [ Links ]
Clarke, V. & Braun, V., 2014, 'Thematic analysis', in A.C. Michalos (ed.), Encyclopaedia of Quality of Life and Well-Being Research, pp. 6626-6628, Springer, Dordrecht.
Cohen, L., Manion, L. & Morrison, K., 2000, 'Research Methods in Education', 5th edn., Routledge Falmer, London.
Cope, D.G., 2014, 'Methods and meanings: Credibility and trustworthiness of qualitative research', Oncology Nursing Forum 41(1), 89-92. [ Links ]
Creswell, J.W., 2012, 'Educational Research: Planning, conducting, and evaluating quantitative and qualitative research', 4th edn., Pearson Education, Inc, New Jersey.
Crowley, M.L., 1987, The van Hiele model of the development of geometric thought, Teaching and Learning, K-12 - 1987 Yearbook, National Council of Teachers of Mathematics, Virginia.
Evbuomwan, D., 2013, 'An investigation into the difficulties faced by Form C students in the learning of transformation geometry in Lesotho secondary schools', Masters' thesis, University of South Africa. [ Links ]
Feza, N. & Webb, P., 2005, 'Assessment standards, van Hiele levels, and grade seven learners' understandings of geometry', Pythagoras 62(1), 36-47. [ Links ]
Flick, U., 2018, An introduction to qualitative research, 6th edn., Sage, London.
Gomes, A., 2011, 'Portuguese pre-service elementary teachers' knowledge of geometric transformations: An exploratory study', in C. Smith (ed.), Proceedings of British Society for Research into Learning of Mathematics, vol. 31, no. 3, pp. 59-64, Oxford University, Oxford.
Gravemeijer, K. & Van Eerde, D., 2009, 'Design research as a means for building a knowledge base for teachers and teaching in mathematics education', The Elementary School Journal 109(5), 510-525. [ Links ]
Graven, M., Hewana, D. & Stott, D., 2013, 'The evolution of an instrument for researching young mathematical dispositions', African Journal of Research in Mathematics, Science and Technology Education 17(1-2), 26-37. https://doi.org/10.1080/10288457.2013.826968 [ Links ]
Guven, B., 2012, 'Using dynamic geometry software to improve eighth grade students' understanding of transformation geometry', Australasian Journal of Educational Technology 28(2), 364-382. [ Links ]
Hansen, A., 2017, Children's errors in mathematics, 4th edn., Sage, Thousand Oaks, CA.
Holmes, V., Miedema, C., Nieuwkoop, L. & Haugen, N., 2013, 'Data-driven intervention: Correcting mathematics students' misconceptions, not mistakes', The Mathematics Educator 23(1), 24-44. [ Links ]
İlaslan, S., 2013, 'Middle school mathematics teachers' problems in teaching transformational geometry and their suggestions for the solution of these problems', Masters' dissertation, Middle East Technical University. [ Links ]
Kaplan, A. & Öztürk, M., 2014, 'Analysis of 2nd-8th grade students' thinking approaches towards understanding the concept of symmetry', Elementary Education Online 13(4), 1502-1515. [ Links ]
Kurt-Birel, G., Deniz, S. & Önel, F., 2020, 'Analysis of primary school teachers' knowledge of geometry', International Electronic Journal of Elementary Education 12(4), 303-309. https://doi.org/10.26822/iejee.2020459459 [ Links ]
Kuzniak, A. & Rauscher, J., 2011, 'How do teachers' approaches to geometric work relate to geometry students' learning difficulties?', Educational Studies in Mathematics 77, 129-147. [ Links ]
Luneta, K., 2008, 'Error discourse in Fundamental Physics and Mathematics: Perspectives of students' misconceptions', in International Council on Education for Teaching (ICET) International Year Book, pp. 385-400, University of Minho, Portugal.
Luneta, K., 2014, 'Foundation phase student teachers' knowledge of space and shape', South African Journal of Childhood Education 4(3), 71-86. https://doi.org/10.4102/sajce.v4i3.228 [ Links ]
Luneta, K., 2015a, 'Issues in communicating mathematically in rural classrooms in South Africa', Journal of Communication 6(1), 1-9. https://doi.org/10.1080/0976691X.2015.11884842 [ Links ]
Luneta, K., 2015b, 'Understanding students' misconceptions: An analysis of final grade 12 examination questions in geometry', Pythagoras 36(1), 261-271. https://doi.org/10.4102/pythagoras.v36i1.261 [ Links ]
Luneta, K. & Makonye, J., 2010, 'Learner errors and misconceptions in elementary analysis: A case study of a grade 12 class in South Africa', Acta Didactica Napocensia 3(3), 35-46. [ Links ]
Makgato, M. & Mji, A., 2006, 'Factors associated with high school learners' poor performance: A spotlight on mathematics and physical science', South African Journal of Education 26(2), 253-256. [ Links ]
Makonye, J.P., 2011, 'Learner mathematical errors in introductory differential calculus tasks: A study of misconceptions in the senior certificate examinations', Unpublished doctoral thesis, University of Johannesburg. [ Links ]
Mateya, M., 2008, 'Using the van Hiele theory to analyse geometrical conceptualisation in Grade 12 learners: A Namibian perspective', Master's thesis, Rhodes University, Grahamstown. [ Links ]
Matteucci, M.C., Corazza, M. & Santagata, R., 2015, 'Learning from errors or not: An analysis of teachers' beliefs about errors and error-handling strategies through questionnaire and video', paper presented at the 9th International Technology, Education, and Development Conference (INTED), Madrid, Spain.
Mayberry, J. (1983). 'The van Hiele levels of geometric thought in undergraduate preservice teachers', Journal for Research in Mathematics Education 14(1), 58-69. [ Links ]
Moss, J., Hawes, Z., Naqvi, S. & Caswell, B., 2015, 'Adapting Japanese lesson study to enhance the teaching and learning of geometry and spatial reasoning in early years classrooms: A case study', The International Journal on Mathematics Education 47(3), 377-390. https://doi.org/10.1007/s11858-015-0679-2 [ Links ]
Mudaly, V. & Rampersad, R., 2013, 'The role of visualisation in learners' conceptual understanding of graphical functional relationships', The African Journal of Research in Mathematics Science and Technology Education 14(1) 36-48. https://doi.org/10.1080/10288457.2010.10740671 [ Links ]
Naidoo, J. & Bansilal, S., 2010, 'Strategies used by grade 12 mathematics learners in transformation geometry', in V. Mudaly (ed.), Proceedings of the eighteenth annual meeting of the Southern African association for research in mathematics, science and technology education, vol. 2: Short papers, pp. 182-190, University of KwaZulu-Natal.
Ndlovu, B.R., 2012, 'Exploring pre-service teachers' knowledge of proof in geometry', Masters dissertation, University of KwaZulu-Natal. [ Links ]
Panaoura, G. & Gagatsis, A., 2009, 'The geometrical reasoning of primary and secondary school students', in The 6th Conference of the European Society for Research in Mathematics Education: Working Group 5, pp. 746-755, Geometrical Thinking, Lyon.
Pegg, J., 1985, 'How children learn geometry: The Van Hiele model', Australian Mathematics Teacher 41(2), 2-4. [ Links ]
Pusey, E.L., 2003, 'The van Hiele model of reasoning in geometry: A literature review', Masters' dissertation, North Carolina State University, Raleigh, North Carolina. [ Links ]
Riccomini, P.J., 2005, 'Identification and remediation of systematic error patterns in subtraction', Learning Disability Quarterly 28(3), 233-242. [ Links ]
Rowland, T. & Ruthven, K. (eds.), 2011, Mathematical knowledge in teaching, Springer, New York, NY.
Schnepper, L.C. & McCoy, L.P., 2013, 'Analysis of misconceptions in high school mathematics', Journal for Teacher Research 15(1), 1-7. [ Links ]
Shalem, Y., Sapire, I. & Sorto, M.A., 2014, 'Teachers' explanations of learners' errors in standardised mathematics assessments', Pythagoras 35(1), 254-264. [ Links ]
Sinclair, N. & Bruce, C., 2015, 'New opportunities in geometry education at the primary school', International Journal of Mathematics Education 47, 319-329. https://doi.org/10.1007/s11858-015-0693-4 [ Links ]
Soon, Y., 1989, 'An investigation of van Hiele-like levels of learning in transformation geometry of secondary school students in Singapore', Unpublished doctoral thesis, The Florida State University. [ Links ]
Spaull, N., 2013, South Africa's education crisis: The quality of education in South Africa 1994-2011, Report commissioned by Centre for Development and Enterprise.
Stols, G., Ferreira, R., Pelser, A., Olivier, W.A., Van der Merwe, A., De Villiers, C. et al., 2015, 'Perceptions and needs of South African mathematics teachers concerning their use of technology for instruction', South African Journal of Education 35(4), 1209-1221. https://doi.org/10.15700/saje.v35n4a1209 [ Links ]
Swan, M., 2014, 'Improving the alignment between values, principles and classroom realities', in Y. Li & G. Lappan (eds.), Mathematics Curriculum in School Education, pp. 621-636. Springer, Dordrecht.
Van Hiele, P.M., 1986, Structure and insight: A theory of mathematics education, Academic Press, Orlando, FL.
Van Putten, S., 2008, 'Levels of thought in geometry of pre-service mathematics educator according to the Van Hiele model', Masters' dissertation, Department of Curriculum Studies, Faculty of Education, University of Pretoria. [ Links ]
Wilkinson, S., 2000, 'Women with breast cancer talking causes: comparing content, biographical and discursive analyses', Feminism & Psychology 10(4), 431-460. [ Links ]
Yilmaz, G. K., Alkan, S., Baran, D., Elmas, H. & Guven, B., 2011, 'Mathematics teachers' views about measurement and evaluation dimension of new Turkish geometry curriculum', Procedia Social and Behavioural Sciences, 15, 2678-2683. [ Links ]
Zehetmeier, D., Böttcher, A., Brüggemann-Klein, A. & Thurner, V., 2015, 'Development of a classification scheme for errors observed in the process of Computer Programming Education', paper presented in the 1st International Conference on Higher Education Advances (HEAd), Valencia Polytechnic University, Valencia, Spain.
Žilková, K., Gunčaga, J. & Kopáčová, J., 2015, '(Mis)conceptions about geometric shapes in pre-service primary teachers', Acta Didactica Napocensia 8(1), 27-36. [ Links ]
 Correspondence:
Correspondence:
Nokwanda Mbusi
Nokwanda.mbusi@ump.ac.za
Received: 06 May 2020
Accepted: 12 May 2021
Published: 30 Sept. 2021














