Services on Demand
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
Pythagoras
On-line version ISSN 2223-7895
Print version ISSN 1012-2346
Pythagoras vol.44 n.1 Cape Town 2023
http://dx.doi.org/10.4102/pythagoras.v44i1.678
ORIGINAL RESEARCH
Exploring the development of South African pre-service teachers' reflective practice
Samukeliso Chikiwa; Mellony Graven
Department of Education, Faculty of Education, Rhodes University, Makhanda, South Africa
ABSTRACT
Ongoing concern about poor learner performance in mathematics has led to wide-ranging research on the subject, globally and in South Africa. Among the remedies identified is the reformation of pre-service teacher (PST) education programmes in a way that supports the acquisition of professional skills for pre-service teachers. Developing PSTs' reflective practice (RP) is a significant component of the desired reformation. Our research explored PSTs' RP development in the context of video-based mathematics lesson analysis. The aim was to contribute knowledge towards strengthening mathematics PST education and to report on whether increased benefits accrued from working with PSTs in small groups, guided by an experienced facilitator, as compared to whole-class lecturing. We draw on this extended analytic framework to compare two sets of reflections written by four selected PSTs based on viewing video recordings of their own teaching. One set was written in August 2018 after the PSTs completed three lecture sessions on RP in a Mathematics Methods course. The other was written in September 2019 after the four selected PSTs participated in three small-group, facilitator-guided sessions. The findings indicate some shifts towards higher-level reflections in the latter set, although only two of the four PSTs reflected at the highest level (reflectivity) following the small-group sessions. Implications for pre-service mathematics teacher education and refinement of frameworks for delineating levels of reflection are discussed.
CONTRIBUTION: The research contributes to mathematics teaching through refining and extending existing models of reflective-based practice to better analyse the shifting nature of mathematics teachers' reflections with a view to supporting improved teaching and learning
Keywords: Mathematics education; reflective practice; pre-service teachers; six-lens framework; pre-service teacher education; reflections; primary school mathematics; foundation phase.
Introduction
There is growing evidence that, despite qualifications, many teachers of primary mathematics do not have sufficient mathematical and pedagogical knowledge for teaching mathematics (e.g. Venkat & Spaull, 2014). This is compounded by the problem that many pre-service teachers (PSTs) come into their degrees with weak mathematical knowledge from their own schooling (Askew et al., 2019). South African teacher education institutions are working on transforming the teaching and learning of mathematics through transforming the ways of preparing mathematics teachers to meet the pedagogical and content knowledge demands of teaching mathematics (see Roberts, 2020, and the PrimTed project). These efforts are influenced by South Africa's long history of poor learner performance in mathematics (Fleisch, 2008; Reddy et al., 2016, 2022; Spaull & Kotze, 2015). The Centre for Development and Enterprise (CDE, 2013) acknowledges that:
[t]he teaching of mathematics in South African schools is amongst the worst in the world. Mounting indicators on school performance and teaching reveal largely unacknowledged poor teaching of mathematics in the great majority of schools. (p. 2)
Developing PSTs' reflective practice (RP) is increasingly being incorporated into pre-service teacher education (PTE) as one of the strategies supporting transformation (Cadiz, 2021). There is, however, limited understanding of how to develop PSTs' RP, particularly in a context such as South Africa, where PSTs appear to have little experience of reflecting (Chikiwa & Graven, 2021). Our study explored the reflections of Foundation Phase (FP) PSTs as they analysed video-recorded mathematics lessons. We chose to focus on FP PSTs because the trajectory of poor performance in mathematics begins at this early stage in South Africa (Spaull & Kotze, 2015). This article reports on a question from a more extensive study that focused on PSTs' RP, namely: What is the nature of PSTs' evolving RP when reflecting on their lessons following small-group, facilitator-led RP sessions? We thus compared the reflections that PSTs developed after engaging in RP in large lecture-type sessions with those they developed after being engaged in small-group sessions under the guidance of facilitators experienced in RP. We aimed to understand the opportunities and challenges of these ways of developing PSTs' RP to inform PTE. While we focus on developing PSTs' RP in respect of the teaching of mathematics, the insights gained may extend to developing RP in other disciplines.
Teaching mathematics is a complex task for many teachers (Ziegler & Loos, 2017), hence Ball, Thames and Phelps (2008) argue for knowledge that is specific to the teaching of mathematics. Inspired by Shulman's (1987) idea of pedagogical content knowledge (PCK), they developed a practice-based framework with six teacher knowledge domains that they argue are necessary for the effective teaching of mathematics which they named 'Mathematical Knowledge for Teaching (MKfT). It is the desire of every mathematics educator to ensure that PSTs leave PTE with adequate MKfT to get started with the teaching of mathematics efficiently. Developing teachers' RP is one approach that has been found helpful in developing teachers' MKfT (Karsenty et al., 2015; Schwarts & Karsenty, 2020). Developing PSTs' RP is included in PTE programmes at our institution and several other South African institutions because of its perceived benefits as a basis for learning from and constantly improving one's teaching (Genor, 2005). As Hutchinson and Allen (1997) noted:
[o]ne of the goals of teacher education is to develop each pre-service teacher into a reflective educator, one who is a life-long learner who perceives every experience as an opportunity for growth, change, and development of understanding. (p. 226)
Developing RP, therefore, becomes a critical element in teacher education programmes. Darling-Hammond (2009) claims that RP functions as a bridge between theory and practice, enabling novice teachers to link the two. Liou (2001) notes that 'critical reflection raises teachers' awareness about teaching, enables [a] deeper understanding of variables related to teaching, and triggers positive changes in their practice' (p. 1). While RP has become a common topic in PTE research and teacher programmes worldwide, there has been less inquiry into the process of developing PSTs' RP. Zeichner (1994) warns that wanting 'to prepare teachers who are reflective does not translate directly into the content of teacher education programs' (p. 9). It is necessary to create a step-by-step process. The challenges in this process may be different for different countries with varying educational systems and cultures of critique; our research sought to contribute within the South African context of PTE.
This article emerges from a broader research study that explored PSTs developing RP through participation in sessions focused on the development of RP through video-based lesson analysis (Chikiwa, 2020) discussed in the methodology section. The article seeks to explore the evolving levels of PSTs' RP when reflecting on their own lessons following small-group, facilitator-led RP sessions.
Understanding reflective practice
Reflective practice is widely noted as key to professional development across various professions (for example healthcare; see Norrie et al., 2012). The professional development of mathematics educators is no exception. Most studies have positively reported on its impact on teaching and learning in mathematics education (Chikiwa, 2020; Darling-Hammond, 2009; Hollingsworth & Clarke, 2017; Karsenty et al., 2015; Ward & McCotter, 2004). Reflective practice enables teachers to meet the learning needs of their classes effectively. It enables teachers to adjust and respond to issues while assisting them to become aware of their underlying beliefs and assumptions about teaching and learning.
The concept of RP can be traced back to 1933, when Dewey first introduced what he called reflective thinking. Dewey (1933) identified three attitudes that lay at the heart of RP for improved efficiency: wholeheartedness, responsibility, and open-mindedness. Wholeheartedness relates to one's commitment to working diligently and seeking every opportunity to learn something new from the present. Responsibility reflects careful consideration of the consequences of one's actions, particularly one's preparedness to acknowledge that the decisions one makes impact the learners' lives in ways both foreseen and unforeseen. Finally, open-mindedness is the willingness to admit the possibility of error, considering various ways of looking at a particular situation or event, and being ready to change one's viewpoint if necessary.
Schon (1983) applied Dewey's notion of RP to the teaching profession and defined RP as the practice by which professionals become aware of their implicit knowledge base and learn from their experience. Several studies have since sought to understand RP in education, exploring its influence in teaching and learning and how to develop it (Beauchamp, 2006; Karsenty et al., 2015; Zeichner, 1994). Beauchamp (2006) carried out a systematic review of 55 articles on RP in search of a comprehensive understanding of the concept. While she could not identify a conclusive definition or meaning, she discovered that scholars agreed about RP's significance as a tool for lifelong learning, professional development and its ability to influence effective teaching. Russell (2005) notes that this absence of consensus should alert teachers and teacher educators that RP is a complex concept that they should approach with caution and preparedness. As Jay and Johnson (2002) put it: 'If the concept itself seems difficult to characterize, it is even more difficult to teach' (p. 73).
The researchers found Dewey's early definition of reflection meaningful and more explicit for teacher education. Dewey (1933) defines reflection as:
[an] active, persistent and careful consideration of any belief or supposed form of knowledge in the light of the ground that supports it … [it] allows individuals to think critically and scientifically. (p. 9)
The process of reflection is thus a systematic cycle that needs constant reiteration. Reflective practice assists teachers in making links between various teaching experiences, thereby fostering progressive learning. Schon (1983) distinguished between 'reflection-in-action', 'reflection-on-action' and 'reflection-for-action' to show how professionals solve problems associated with the practice. Olteanu (2017) summarises as follows:
Reflection-in-action takes place during an action, and reflection-on-action takes place after an event has occurred. … Reflection-for-action is thinking about future actions with the intention of improving or changing a practice. This type of reflection requires teachers to anticipate what will occur during a lesson, as well as reflect on their past experiences, before a lesson occurs (Farrell 2015). The main problem teachers have in doing reflection-for-action is knowing what they should reflect on to be able to make improvements or changes in their own practice. (p. 350)
Schon (1983) uses the phrase 'knowing in action' to describe tacit knowledge that develops as teachers reflect on their practice. He likens it to riding a bike. If a person is riding a bicycle, and starts to fall, they will react in situ to regain their balance, yet may not be able to explain how when asked about it. Reflective practice facilitates knowing in action and hence constitutes a basic part of teaching and learning. Selmo and Orsenigob (2014) concur that 'learning from experience is enriched by reflecting on experience' (p. 1925). It is therefore imperative that PSTs develop the skill to reflect on the practice of teaching, and that at least part of this development should occur within the actual practice of teaching. Mewborn (1999) claims that this will create a 'bridge across the chasm between educational theory and practice' (p. 317).
Because of the many benefits associated with developing teachers' RP, PTE programmes have increasingly embraced it as a useful means of preparing teachers for effective teaching. Kullman (1998) claims it leads 'to a greater awareness among student teachers of what constitutes appropriate pedagogic practice and will lay the foundations for development, a process which will be ongoing throughout their teaching careers' (pp. 471-472). According to Shoffener (2009), exposing PSTs to RP during teacher preparation supports their construction of the personal knowledge they need to guide their teaching and learning decisions. She further claims that 'by engaging in reflective thinking, pre-service teachers (PSTs) generate questions and, by seeking answers, support change in their educational actions, responses to criticism, and social and cultural beliefs' (p. 145). A key challenge for PTE however is that PSTs are mostly outside of the classroom and not themselves teaching. In this respect creative ways need to be found for PSTs to develop key RP skills to support their knowing in action in classroom teaching.
Studies conducted with PSTs confirm some benefits of RP in PTE with the use of video-recorded lessons. For instance, Hewitt et al. (2003) explored how PSTs reacted to scenarios shown in video-recorded lessons and confirmed that this video-stimulated reflective approach helped PSTs develop deeper insights into classroom practice. Similarly, Chen (2016) included reflection as part of the design of a teaching-learning programme for training kindergarten PSTs to teach mathematics. Her study concludes that engaging PSTs in RP can assist them to gain mathematical knowledge and learn more about their own teaching methods. However, not all methods and attempts to develop RP with PSTs have proved successful. For example, PTE efforts to involve PSTs in reflective journal writing have been found to be relatively ineffectual. Ward and McCotter (2004) claim that most PSTs do badly in reflective writing assignments because they do not understand what reflection is or how to practise it. Research studies have therefore raised questions about the widespread practice of writing as a means of developing RP (Shoffener, 2009; Ward & McCotter, 2004). Thus, while there is general acknowledgement of the value of developing this practice in PSTs there is not general agreement on optimal ways to do this, and research tends to note that this is a relatively challenging skill to develop effectively.
Teacher education remains actively in search of strategies for developing PSTs' RP. Karsenty et al. (2015) explored video-based mathematics lesson analysis using the 'six-lens framework' (SLF) to develop in-service teachers' RP and MKfT and reported positive results. Their ongoing research continues to gather evidence, and deepen our understanding, of the effectiveness and opportunities that such a tool can provide in developing RP (see, for example, Karsenty, 2018; Karsenty & Arcavi, 2017). While other researchers have similarly used video to stimulate reflection on practice (e.g. Hollingsworth & Clarke, 2017) we draw on the work of Karsenty and colleagues because their SLF was used as a tool to support the PSTs in this study in their reflections on the video.
Theoretical framing and the six-lens framework
Our research was underpinned by Vygotsky's (1978) social cultural theory of learning guided by the assumptions that social interactions play an essential role in learning; language is a fundamental tool in the learning process and learning occurs within the zone of proximal development (ZPD) and is mediated by more knowledgeable others (MKO). A MKO can be a teacher, peer or artefact that embodies cultural or historical knowledge and functions to draw learners into their ZPD (Abtahi et al., 2017; Graven & Lerman, 2014). The ZPD is described by Vygotsky (1978) as:
the distance between the actual developmental level as determined by independent problem solving and the level of potential development as determined through problem solving under adult guidance or in collaboration with more capable peers. (p. 86)
The work of Karsenty and colleagues coheres with this framework as it emphasises social learning and the importance of careful mediation in the use of video of teaching practice as an artefact for development. Karsenty et al. (2015) and colleagues designed the SLF in collaboration with teachers. They designed it as a tool primarily for their VIDEO-LM project (Viewing, Investigating and Discussing Environments of Learning Mathematics) at the Weizmann Institute of Science in Israel to enhance secondary school mathematics teachers' reflection and MKfT. The tool comprises six viewing lenses that the team considered essential for analysing and reflecting on episodes of mathematics teaching. These are mathematical and meta-mathematical ideas (MMI), teachers' explicit and implicit goals, tasks and activities, dilemmas and decision-making (DDM), interactions with learners, and teachers' beliefs.
The lenses provide the PSTs with opportunities to consider concepts that can be developed under a given topic. Karsenty et al. (2015) designed the MMI lens to guide the focus to the mathematical concepts and procedures the videoed teacher is advancing through the lesson. Karsenty and Arcavi (2017, p. 441) claim that reflecting on MMI 'not only enables teachers to overtly explore ideas related to a certain topic; it also helps to refine, rethink and re-connect among them, and sometimes even to learn something new'. The goals lens directs the viewers to consider the explicit and implicit goals the teacher sought to achieve through the lesson. Reflecting through this lens not only assists the viewing PSTs to understand the teachers' actions and decisions, but also alerts them to the significance of setting meaningful goals. The tasks are the activities the teacher engages in to pursue the goals. Reflecting on these exposes the PSTs to both content and strategies for teaching mathematics. The interactions lens focuses on how the teacher was interacting with the learners during the lesson, such as how they introduce the problems and activities, and respond to learners' spoken and unspoken concerns. Reflecting through this lens exposes PSTs to different ways of interacting with learners and allows them to evaluate what methods work better. The DDM lens helps viewers identify the possible dilemmas (unexpected challenges) during the lesson and what decisions the teacher makes concerning these. The teacher responds to unexpected behaviours (relating to the teaching and learning of mathematics) and learners' responses to tasks and activities, during the lesson. Lastly, the beliefs lens calls attention to the teacher's beliefs about mathematics teaching that are displayed through how the teacher conducts the lesson. The teaching approaches chosen by the teacher for the lesson provide insight into their beliefs about the subject and how it should be taught. Exposure to different teacher beliefs may help the PSTs develop a new conception of the subject and develop better ways of teaching it.
While the framework may appear straightforward for experienced teachers, it should be remembered that PSTs have almost no teaching experience other than practicum and are still in the process of developing their MKfT.
Methodology
The research paradigm adopted was interpretive guided by the assumption that reality is multiple and shaped by social experiences (Cohen et al. 2011). We used a qualitative case study research approach (Creswell, 2014) gathering data in the form of RP written narratives. The case our article is focused on is a group of four PSTs participating in small-group RP sessions. Phase 1 of our research included 19 out of 52 third-year PSTs who agreed to participate in the study. Phase 2 was with only 4 of the 19 PSTs who were purposefully selected on the basis that they each had submitted a video recording of the mathematics lesson they taught during teaching practice as part of their course assignments. These video recordings of their own teaching provided a rich video resource for self- reflection. While five PSTs had submitted such video recordings, only four agreed to participate in the further sessions of Phase 2 of the research. The focus of the article is on the data collected with the four PSTs in Phase 2.
These sessions with the four PSTs began at the end of 2018 following Phase 1 of our research.
In 2018, 52 PSTs, in their third year of Bachelor of Education studies at a university in South Africa were taken through three sessions of analysing video-recorded mathematics lessons with the intention of developing both their MKfT and their RP. The lecturer participating in our study identified the need for drawing on support tools to aid PSTs' reflection on video lessons. Having come across the SLF of Karsenty and colleagues she chose to draw on this tool as a device to support PSTs in focusing on a range of important aspects of video-recorded mathematics lessons as they reflected on them. Since the aim of the sessions was to develop the PSTs' MKfT and RP, we took the opportunity to investigate how the PSTs fared with RP directed to mathematics education. In the whole-class RP sessions, the lecturer started by introducing the SLF, and asked the PSTs to reflect on video-recorded mathematics lessons she perceived to be relevant to the PSTs' context. She asked different groups of PSTs to use different lenses from the SLF to discuss and report back reflections relevant to each lens. The PSTs were requested to write individual reflections before they could discuss as a group, then present to the whole class, leading to a class discussion. Thus, PSTs were given opportunities to co-create knowledge and learn from each other.
All 52 PSTs in the cohort were invited to participate in the research and all ethical protocols were followed. Nineteen PSTs volunteered and signed consent forms for Phase 1. The PSTs were provided anonymity and were informed they could withdraw their participation at any point. The ethics application was approved by our university Education Research Ethics Committee in 2017. Elsewhere (Chikiwa & Graven, 2019, 2021) we have focused on the written reflections of 19 PSTs who participated in the broader study in Term 1 and Term 2 of 2018. The findings pointed to generally low levels of reflection and few shifts towards higher levels of RP. The focus of this article is on Phase 2 which began towards the end of 2018 and continued in 2019 with four of these PSTs who had made video recordings of their own mathematics teaching practice during their teaching practicum as part of the practicum assessment. (The PSTs were requested by their lecturer to video-record themselves teaching any subject of choice and submit to the practicum coordinator for assessment.)
In Phase 2 we asked the four PSTs to write reflections on these videos of their own teaching using the SLF they had used in lectures during 2018. They submitted these written reflections to us in the last term of 2018. In the third term of 2019 we invited the same four PSTs to participate in three small-group, facilitator-led RP sessions focused on selected video episodes of other teachers' lessons as a way of scaffolding their RP skills. The video lessons used during these sessions were chosen by the facilitators for their appropriateness to FP teaching as well as their experience of these lesson videos having rich material to stimulate reflective discussion. The facilitators, being experienced in reflecting on video of mathematics lessons according to the SLF, served as the mediating MKOs, modelling RP focused on important mathematical aspects of teaching and learning. Following these sessions (September 2019), the four PSTs were asked to use the SLF once again to provide written reflections on the video recording of their own lesson they used previously in 2018. They completed these towards the end of the fourth term in 2019. We analysed their reflections using content analysis (Stemler, 2015) and a tool we developed comprising four hierarchical levels of reflection that we adapted from existing frameworks of reflection levels. Note that the SLF was a pedagogical tool used by the lecturer for focusing attention on six different aspects of lessons while the framework we use for analysis relates to analysing the levels of reflection when PSTs reflect using the various lenses. (This is discussed further in the section that follows and is summarised in Table 3.)
As mentioned above, in Phase 2 the four PSTs were taken through three reflection sessions led by experienced facilitators to support their RP development. In these sessions the facilitator probed for reflections as the PSTs analysed selected video recordings of other teachers' mathematics lessons. In Table 1 we share an excerpt from one of the sessions showing how the facilitator probed for deeper reflections.
At the start of the session the facilitator Carol (who was highly experienced in the use of the SLF for supporting teacher reflection on videos) provided some orienting comments that included an explicit statement about the importance of noticing mathematical over general aspects of lessons, such as:
'Our focus is on the mathematics, so we try to talk less about generic aspects such as the teacher's voice or the teacher's body language; these things are interesting [but] … our focus is to talk about the mathematics. So the mathematical idea, the mathematical goals, the mathematical activities, even the interactions can be about the mathematics, so the mathematics is in the centre.' (Carol)
Thereafter she assigned each of the PSTs a metaphorical lens to look through as they analysed the video-recorded mathematics lesson she had selected for the session. She played the video and allowed the PSTs to write reflections using the lenses they were assigned. She began the discussion by calling for more reflections through probing questions. In the process she assisted the PSTs by guiding them to comment on aspects of the lesson specific to each lens. In Table 1 we share some examples of interactions between the PSTs and the facilitator.
As seen in the session excerpts in Table 1, the facilitator introduced the session by encouraging the PSTs to focus on the mathematical aspects of the lesson. As the session continued, she asked PSTs questions that related to each lens of the SLF through which the PST was asked to analyse the lesson. The facilitator probed for deeper insights into what was happening in the lesson and why.
After three such sessions focusing on different videos, we asked the four PSTs to provide written reflections again on the video recordings of their own teaching (which they had done a year earlier). We then analysed their written reflections using the four levels of reflection framework (FLRM) and compared their first reflections on their own practice (ROP1 in 2018) with their second (ROP2 in 2019). Below we give a brief account of how we developed our analytical framework.
Developing the four levels of reflection framework for analysing reflections
The literature offers a wide range of useful analytical frameworks for analysing RP, but none of them quite met our needs in relation to coding and analysing written reflections of the 19 PSTs who participated in Phase 1 of the study. We therefore had to create our own, merging and adapting existing frameworks following a detailed and wide-ranging review of existing frameworks. We began by merging elements of Lee's (2005) and Muir and Beswick's (2007) levels of reflection frameworks (these resonated most strongly with the nature of the data we had) to develop a basic hierarchical RP tool for analysis with indicators. Following repeated revisions to our initial framework (from ongoing analysis of samples of PSTs' data over time) we finally settled on a four-level framework that merged key elements of both Lee and Muir and Beswick's three-level frameworks and indicators.
After using samples of data in these two combined frameworks we identified the need for an additional level in our framework as well as some refinement of a set of sub-indicators across the levels. We particularly noted that 'suggestion' (as evidenced by our data) did not cater for reflectivity or critical reflection in its full sense as described by Lee (2005) and Muir and Beswick (2007). We therefore created a level between their levels 2 and 3 which we named Suggestions, and this shifted their third and last level to level 4 in our framework. We concurred with Lee's idea that reflectivity should go beyond identifying a classroom event and providing explanations and suggestions, to a deeper engagement with the identified event that enables the proposal of alternatives. We thus adopted Lee's level 3, Reflectivity, as our highest level of reflection. (See Chikiwa and Graven, 2021, for the rationale for the need to extend to this four-level framework.) In Table 2 we present the four levels comprising our adapted RP framework. In the third column we provide what we consider to be the key indicators for each level (adapted from the aforementioned frameworks) and in the fourth column we provide some examples from the PSTs' written reflections.
We used the FLRM that we developed to analyse our data. Each statement written by the PST was broken into small chunks of single ideas to allow for coding. The chunked data was levelled against the levels of reflection in the FLRM. The PSTs' reflections were either general or mathematical, which led us to code each idea as such. General reflections referred to reflections that were not specific to the teaching and learning of mathematics but generally applicable to the teaching and learning of any subject, for example 'The teacher put learners in groups of four'. A reflection was deemed to be general when the PST did not make mention of mathematical concepts, terms, symbols, numbers, or mathematical ideas.
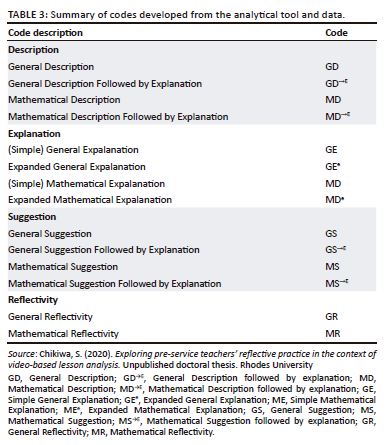
We referred to mathematical reflections as reflections that were specific to the teaching and learning of mathematics. These were evidenced by explicit mention of the mathematical concepts, terms, numbers, symbols or ideas, for example 'The teacher wrote 39+9 on the board', or when an implicit reference is made to mathematical terms, numbers, symbols or ideas, such as 'The learners did this activity in groups'. If the activity that is described before this statement was mathematical, then the reflection also becomes mathematical because of the reference. Following a process of repeated refinement of codes we settled on the codes in Table 3 that we subsequently used for coding all the PSTs' data.
We identified the codes that have an arrow with 'E' as indicative that the reflection was followed by an explanation. For example:
'[The teacher] wrote the addition steps on the board MD→E, to help the child that did not understand ME.' (Lutho, ROP1, DDM, ref 44-45)
'A simple explanation is when the rationale given was a statement with only one idea (like the one above). The expanded explanation was a rationale with more than one idea. For example:
'I shouldn't have put together addition and subtraction MS→E, because learners were not really focused and couldn't understand the subtraction part, they needed it to be done separately MEe.' (Bonga ROP2, ref 80-81)
As in the establishment of the levels of RP and the indicators thereof, these codes were similarly developed after several rounds of coding by the authors of the article along with a third researcher who was brought in to assist in establishing whether our coding and indicators were sufficiently recognisable to others to enable consistent coding across researchers. Some initial differences in coding resulted in further refining and clarification of the codes until there was general agreement between the researchers' coding. Thereafter the first author of this article coded each of the four PSTs' reflections. The second author served to check agreement with the coding and small discrepancies were resolved through discussion and through reverting to the indicators and providing further clarification where necessary. Below we present the comparisons we made for each of the four PSTs (in alphabetical order of their pseudonyms).
The findings
In this section we share both quantitative and qualitative data from our coding of two sets of reflections written by PSTs a year apart. The tables in each figure capture the quantitative descriptive statistics following the coding of all the written reflections, according to levels of reflection and according to mathematical versus general reflections. The pie charts following the tables compare the PSTs' general versus mathematical reflections on each set of data.
Following the figures that summarise each of the four PSTs data we provide selected qualitative data that exemplifies and illuminates shifts from the first (ROP1) to the second (ROP2) written reflections.
Comparing Bonga's 2018 and 2019 reflections on his own practice
Figure 1 contains summaries of Bonga's ROP1 and ROP2 on the same video-recorded lesson, followed by a discussion of the comparison across the years.
While we see a small decrease in the total number of ideas that were coded in Bonga's ROP1 (100) to the number of ideas in ROP2 (92), Figure 1 shows that Bonga's Level 1 descriptive reflections shifted downwards from 86% to 77% and his explanation of Level 2 reflections increased slightly from 14% to 16%. The decrease in the proportion of descriptions is mostly balanced by the 7% presence of mathematical suggestions in ROP2 while there were no suggestions in ROP1.
In ROP2 across the lenses, Bonga supported a few more of his mathematical descriptions with explanations. Excerpt 1 below provides an example of his reflections on MMI in ROP1 and ROP2 to illuminate the modest shift towards increased explanation. No suggestions were provided in either ROP1 or ROP2 for the lens of MMI. We have highlighted the explanations in both:
'In this lesson I planned to teach learners bonds of 15 (MD). I wanted learners to come up with two numbers that can be added to make up the number 15 (MD). Each learner would raise a hand (GD) and give the two numbers (MD), explain to the class how they calculated it (MD). Learners had to justify their answers by explaining to the class (MD→E) This was for helping them to have number sense, to help them with addition (MEe) Aims of this lesson was to equip my learners with 'adding on' instead of starting from 1 when adding (MD). As learners were explaining how they arrived at making 15 with two digits (MD), I helped them to start with the larger number instead of small number to do so (MD).' (Bonga ROP1, MMI, ref 1-10)
'In this lesson I taught learners bonds of 15 (MD→E). This was to help learners know different numbers that make up the number 15 (ME) so that they can add or subtract faster without counters (MEe). Learners had to come up with 2 digit that would make 15 (MD). This was first done as whole class (GD), learners giving the teacher numbers (MD) and showing how they arrived to their answer (MD). Justifying their answer (MD) and showing their calculations (MD→E) helped learners understand their procedures (ME). Then we did it using a grid (MD). The grid had addition on it (MD→E). We used it [the grid] to look at different ways to add (ME), mainly adding on (MD). The second strategy was number line (MD); here I introduced subtraction (MD).' (Bonga ROP2, MMI, ref 1-16)
Through the MMI lens, which is focused on mathematical and meta-mathematical ideas, as expected, the reflections for both ROP1 and ROP2 are predominantly mathematical. Across other lenses we see a shift towards more mathematical than general reflection ideas. The tables and pie charts in Figure 1 show a significant shift in Bonga's reflections towards mathematical ideas, from 45% in ROP1 to 84% in ROP2. Thus, in ROP2 Bonga focused more on mathematical descriptions and explanations across the lenses. For example, while Bonga provided several similar descriptive reflections on his beliefs in relation to the lesson observed in both ROP1 and ROP2, the start of the ROP2 reflection indicates an orientation towards increasingly foregrounding the specificity of teaching mathematics. For example, in ROP1 'Beliefs' Bonga begins his reflection with 'Any discipline can be made fun by a teacher (GD), it's all just a time needed to be taken by the teacher (GD) and willingness to allow the children play as they learn (GD)'.On the other hand, for ROP2, Bonga begins with 'Maths can be done in different ways (MD). It can be hard for others (MD) and easy for others (MD). Learners have to be able to justify (GD) and show how they got to an answer (GD)'.
Of particular interest is that all Bonga's suggestions (L3) are mathematical rather than general. While no suggestions appear in ROP1, several emerge in ROP2. For example, in the Task lens of ROP2 Bonga follows his description of learners using other learners' fingers to count with: 'I should have provided counters for my struggling learners'. In addition, following his reflections on each of the six lenses in ROP2, Bonga took the initiative to add a section, namely 'What would I change?'. Of interest is that all ideas included here are mathematical:
'I shouldn't have put together addition and subtraction (MS→E), because learners were not really focused (ME) and couldn't understand the subtraction part (ME), they needed it to be done separately (MS→E). These two [algorithms] are already complicated for Grade 1 to use on 2-digit numbers ME, and putting them together was not a good idea (MS→E) because I ended up spending more time on addition and very less time on subtraction (ME). Many learners seemed to get confused when I wanted them to subtract (MD). That was not good for the learners (MD). They didn't learn much from it (MD). I should have stuck with only one (MS).' (Bonga, ROP2, Beliefs, Ref, 80-87)
In the above paragraph we see that Bonga brings several L1 (descriptions), L2 (explanations), and L3 (suggestions) into dialogue with each other. When these were considered as a whole, we decided that the paragraph constituted an example of L4 reflectivity. Recall that our definition of reflectivity requires that PSTs engage dialogically with the classroom event; it incorporates suggestions that are considered from different perspectives. We noted here that Bonga brings observations, descriptions, explanations, suggestions, and justifications for these into dialogue, constituting L4 reflectivity. Thus, while no single idea is coded as reflectivity, the paragraph as a whole constitutes reflectivity. For this reason, we have placed L4 as separate from the total L1, L2, and L3 ideas coded and we have put NA in the table under the percentage for reflectivity.
As this instance (and two cases in Joy's reflections) were the only reflections across the data sets that met the indicators for reflectivity, we did not have sufficient data to expand the sensitivity of our coding system for this level of reflection. The idea that multiple ideas together display reflectivity, rather than a single utterance or idea, suggests further consideration is needed in terms of how this L4 of the reflection framework subsumes (is constituted by) L1, L2, and L3 utterances, rather than having its own distinct utterances.
The above shifts suggest that the facilitator-guided reflection sessions may have influenced Bonga's attention to focus on mathematical learning and teaching aspects of the lesson, and to extend his response to include engaging with some reflectivity, particularly in relation to engaging with suggestions and explanations (or justifications) for these suggestions. This was not however the case across PSTs, as we see in Dumi's reflections in Figure 2.
Comparing Dumi's 2018 and 2019 reflections on his own practice
Figure 2 contains summaries of Dumi's ROP1 and ROP2 on the same video-recorded lesson, followed by a discussion of the comparison across the years.
As seen in Figure 2 there was a drop in the number of ideas coded in Dumi's reflections from ROP1 to ROP2 (109 to 73). In ROP2 Dumi avoided reflecting on classroom management as he had done in ROP1. While the total number of reflection ideas went down, the coding shows a proportional shift towards less description (80% to 66%) and more explanation (14% to 29%), while the suggestions remain relatively consistent across both ROP1 and ROP2 (at 6% in ROP1 and 5% in ROP2). A considerable number of his reflections in ROP2 were followed by explicit explanations (see Figure 2, ROP2) as evidenced by his repeated use of the phrase 'reason is that'. No paragraphs were considered at the level of reflectivity (L4). Thus, the greatest shift for Dumi was towards a greater proportion of explanatory reflections. To illuminate this proportional shift towards more explanation, we share his ROP1 and ROP2 on 'Interactions with students'. Dumi's explicit indication that he was providing reasons in ROP2 ('the reason is / for that') was not visible in ROP1. This probably suggests the impact of the facilitators' probing for reasons behind identified events:
'First of all, I was walking around the classroom (GD), helping learners who had questions (GD) and those who were stuck (GD). I was addressing them as a group since I grouped them (GD), but I noticed that some of them were confused (GD), I decided to sit with them one on one (GD). The time was a problem (GD→E) because, I ended up spending lot of time with some students (GE) while others were struggling (GD) and I couldn't finish all of them to see whether they were following the activity (GD). The questions that I was asking to students, some of them were questions like: if you have 12 dominos and added 7 dominos, how many of them in total (MD). I also told them that addition means putting together (MD 68) and subtraction means taking away (MD). Some of the students had questions revolving around how to use the counters (MD). Some they were not familiar on how to use them [counters] (MD). I also had a rule that, when I speak they should listen (GD) and when someone wants to speak must raise their hands (GD→E) so that I can give, there is order in class (GE). Even though the class was a little bit chaotic (GD) when I was busy with a group of students (GD) some would make noise (GD).' (Dumi, ROP1, Interactions, ref 56-76)
'Firstly the teacher is explaining the lesson to the whole class (GD→E), reason [for] him to do this he wants everyone to listen and pay attention on the instructions, so he does not waste time during the lesson (GEe3). He grouped them into three groups (GD) and gave each group different task (GD) and material to do (GD) and use (GD→E). Reason is that he was developing different strategies for each group (GE). Teacher is moving to each group (GD→E) to ensure that everyone understand the instructions and they are doing what they supposed to be doing (GEe2). The teacher is asking learners during the lesson in each group questions such as: show me how did you do it? Double check is the answer is right, how did you calculate it? (GD→E) Reason is that he wants them to make sure that they know how they got the answer. He also wants them to self-correct themselves (GEe). He kept on saying yes as his response (GD→E) to show that he is listening to the learners and he wants them to carry on (GEe2). He encourages learners to do different sums (MD→E) to develop different strategies of calculating and understanding the operations (GEe2). Teacher also instructing learners to help each other (MD→E). Reason for this is some learners understand it better when they get help from peers and some are developing confidence in mathematics (MEe3). He encourages them by saying good to learners who are doing well (GD→E) reason for this he wants them to give their best and even if they fail, they cannot be afraid to try hard (GEe2). He also instructs learners to recount when they have forgotten a number (MD→E) so that they remember which number follows what (ME).' (Dumi, ROP2, Interactions, ref 1-20)
In terms of the mathematical and general foci, there was an unexpected shift away from reflecting on mathematical events towards more general events. The mathematical reflections decreased from 59% in 2018 to 41% in 2019. This could be a result of the keen interest he displayed in the lens of interaction with students, which generally motivates reflections that are more general than mathematical (see Chikiwa & Graven, 2022). This interest is echoed in that he began his ROP2 by reflecting on 'interactions' instead of the MMI that is presented first in the framework and therefore commonly used first. He also wrote more reflections under this lens than the rest. Thus, it may seem that the three sessions of facilitator-guided reflections did not shift Dumi's focus to mathematical reflections or increase his suggestions and reflectivity, though the move to providing more explanation could have been supported by these sessions.
Comparing Joy's 2018 and 2019 reflections on her own practice
Figure 3 contains summaries of Joy's ROP1 and ROP2 on the same video-recorded lesson, followed by a discussion of the comparison across the years.
Unlike Bonga and Dumi, there was an increase in the quantity of Joy's coded ideas from 58 in ROP1 to 97 in ROP2. Thus, Joy wrote more ideas about her teaching after the facilitator-guided sessions. Joy's reflections shifted steadily to higher levels after the series of facilitator-guided sessions. As seen in Figure 3, there was a noticeable decrease in the percentage of descriptions (L1) from 76% in ROP1 to 63% in ROP2, and a commensurate increase in explanations (L2) from 17% to 24%. The proportion of suggestions (L3) also increased from 7% to 13%. We share an example of her reflections in ROP1 and ROP2 for the 'Tasks' lens to illustrate some of the subtle shifts towards more explanation:
'Rote counting in 10s (MD). Mental maths activity - number plus 2 (MD), Measuring desks using pencils (MD). Writing down their measurement observation in their workbooks (MD). I asked the learners leading questions (GD→E)so as to scaffold them (GE). Sometimes the learners would not understand what answer I was looking for (GD). In rote counting, as mentioned before some of the learners were not counting correctly (MD) or even counting at all (MD). But that was difficult for me to pick up (MD). By doing the mental maths activity (MD→E) they got to revise on their addition skills (ME). They did the measuring activity (MD→E) so that they got to see how many pencils can fit into the length of their desk (ME) They should have written their observation in their workbooks (GS→E). The benefits of this are they get to connect what they observe with writing it down, a form of report (GE).' (Joy, ROP1, Tasks, ref 29-43)
'I introduced the task by asking questions (MD→E) so that I could see how much they knew about measurement (ME). The responses were accurate (GD) but only came through once I started asking leading questions (GD). This showed me that they had an idea of what measurement was (MD) but did not connect the concept to their prior knowledge (MD). I then demonstrated what I wanted them to do by using the board (GD) instead of using a desk and a pencil which they were also using for measuring (MD). Using the board may have confused some of the learners (MD→E)because I just started to [measure] what may have looked like at the middle of the board which we see when two learners start measuring their desk in the middle (MEe).' (Joy, ROP2, Tasks, ref 37-63)
'I used the board (GD→E) because I wanted the entire class to see what I was demonstrating (GE), but in the process, I took it for granted that I was starting in the middle of the entire board (GD). A clearer demonstration could have avoided this (GS) paired up with a clearer instruction (GS). Using this practical way of teaching could be beneficial to the learners (GS→E) because they can see and do what I am explaining in the abstract (GEe). Demonstrating how to measure would have been ideal (MS→E) because they would ideally be able to link it to daily activities of measurement (ME).' (Joy, ROP2, Tasks, ref 37-63)
'The potential shortfall is the form in which I communicated the instruction (GS1). The writing as consolidation of the activity (MD→E) was to create a link between measuring and recording (ME). However, next time I would combine the recording with the measuring (MS→E) so as to improve this part of the lesson (ME). I will ask one learner to measure (MS) and the other to record (MS→E). This is because the time between them measuring and me handing out their books may be too long for others to remember what they had measured (MEe).' (Joy, ROP2, Tasks, ref 37-63)
Elaborating in ROP2, Joy followed most of her described classroom events with a rationale or explanation. She further made several mathematical and general suggestions for improving future instruction whereas in ROP1 she had only provided a single general suggestion. In ROP2 she reflected with intention to improve instruction, which we see as probably a result of participation in the facilitator-guided sessions. We also found that in ROP2 Joy wrote two reflections at L4: GR (highlighted in the excerpt above) and MR. As mentioned in Bonga's section, L4 reflectivity constitutes a collection of reflections (description, explanation, and suggestion) that together are in dialogue with each other and at the level of paragraph.
The second and third paragraphs in ROP2 above point to possible instances of reflectivity. In the first instance of reflectivity, Joy is having a dialogue with herself about how she used the board in a manner that hindered the learners' conceptual understanding of measurement. She ends the dialogue with a proposal that carrying out a demonstration accurately would have helped learners to link measurement with daily activities. In the second instance of reflectivity, Joy again enters self-dialogue, reflecting on the 'less than ideal' way she taught the learners. She provides her reason for her judgement and suggests a way forward also backed by reason. The excerpts provide some examples of the qualitative shifts in Joy's reflection between the two years. The proportion of mathematical (versus general) reflections remained relatively consistent across ROP1 and ROP2 at 63% to 59%.
Comparing Lutho's 2018 and 2019 reflections on her own practice
Figure 4 contains summaries of Lutho's ROP1 and ROP2 on the same video-recorded lesson, followed by a discussion of the comparison across the years.
There was a small increase in the quantity of Lutho's reflections between 2018 and 2019, from 61 to 63. In ROP2 more attention was paid to some lenses while attention was removed from others. For example, Lutho's MMI reflections increased from 8 in 2018 to 14 in 2019, while her reflections on interaction halved from 12 in 2018 to 6 in 2019. As in Joy's case, we noticed steady shifts from the lower levels to higher levels of reflection. As seen in Figure 4, L1 reflections decreased significantly from 90% to 75%, a shift complemented by an increase in L2 reflections from 10% to 16% and L3 reflections from 0% to 9%. There were no instances of reflectivity. We also noticed a slight shift to a more mathematical focus than general. Mathematical reflections increased slightly from 57% in 2018 to 63% in 2019, while general reflections decreased from 43% to 37%. The shift in Lutho's reflections from lower to higher levels and to mathematical events of her lesson seems to point to the positive influence of facilitator-guided reflection sessions on Lutho's RP. We share her ROP1 and ROP2 reflections on MMI to illustrate how in ROP2 she followed her described classroom events (that were similarly described in ROP1) with explanations and went further to suggest what could possibly improve future instruction.
'The teacher brought forward the money concept (MD). The aim was to teach about the currency used in SA [South Africa] (MD). This is evident through her use of a chart (MD) and the different pictures of monies (MD) that she uses as manipulative materials for the children (GD→E) to acquire concrete understanding (GE). In her teaching she incorporated addition (MD) when asking children how much money is needed to produce a certain amount (MD).' (Lutho, ROP1, MMI, ref 1-8)
'[The lesson was on] SA money currency (MD and value (MD). [That is, identification (MD) and recognition of currencies of different currencies (MD)]. She used a chart to create a pictorial of what money looks like (MD→E) for the children to see (GE). Using the chart (MD→E) allows them to link the pictures that are in the chart and the manipulatives that are in front of them (ME). Nonetheless, she could have allowed the children to explore the manipulatives themselves before she showed them the chart (MS→E) to check how much understanding of money do they already have (ME). She allows the children to find the correct currency by themselves (MD) after seeing the picture of that currency (MD→E). This helps the children to acquire concrete understanding of what the different currencies look like (ME). On the other hand all children with different intelligences are catered for (GD).' (Lutho, ROP2, MMI, ref 1-14)
Findings and discussion across the four pre-service teachers
The overview of the four PSTs' reflections shows that for all PSTs there was an increase in the proportional percentage of ideas that went beyond L1 descriptive reflections. Thus, there was a greater proportion of explanations (L2) and suggestions (L3) from ROP1 to ROP2 for all four of the PSTs, other than Dumi, whose percentage of suggestions remained relatively constant (6% in ROP1 and 5% in ROP2). Two of the PSTs, Bonga and Lutho, had not provided any suggestions in ROP1 and provided several in ROP2. Furthermore, while no examples of L4 reflectivity reflections were found in ROP1, in ROP2 three examples are found in which Bonga and Joy each engaged with descriptions, explanations and suggestions in a dialogic way that met our definition of reflectivity.
As far as the mathematical versus general balance of reflections is concerned, despite the explicit orientation in facilitator-mediated sessions towards a focus on mathematical rather than generic observations of lesson events, only Bonga's and Lutho's mathematical reflections shifted upwards. Bonga's mathematical reflections increased significantly, from 55% to 84%, while Lutho had a shift from 57% to 63%. The other two PSTs' proportional focus on mathematical ideas decreased slightly from ROP1 to ROP2, although only for Dumi did this result in his focusing more on general than mathematical ideas in ROP2 (59% general vs 41% mathematical). For all others, mathematical reflections continued to dominate over general reflections (59%, 63% and 84% for Joy, Lutho and Bonga).
The above suggests that the facilitator-guided reflections (and perhaps the increased experience in both practicum and studies) supported shifts towards increased explanation and suggestion for the PSTs in ROP2. This said, descriptive (L1) reflections still dominated at between 63% and 77% of PSTs' coded reflection ideas in ROP2.
Thus, across the four PSTs, reflections were still predominantly at the lowest level of reflection (description) with only modest shifts for some towards a greater proportion of higher-level reflections. This suggests that while small-group, facilitator-guided reflection sessions may be helpful in supporting some PSTs to provide occasional suggestions and instances of reflectivity, more work is needed if we wish to shift PSTs' RP towards the deeper reflectivity needed for strengthening MKfT and allowing for transformation of practice. Therefore, while our findings provide some support for the finding of Johns (2010), who reported that facilitator-guided reflection assists novice practitioners to improve the way they reflect, the extent of this assistance appears relatively limited in the case of only a few facilitator-guided sessions. These findings of shifts across the four PSTs' reflections on their own practice following three facilitator-guided sessions are similar to the limited shifts in levels of RP identified with the larger sample of 18 PSTs following three lecture sessions on the use of the SLF for developing RP using video-recorded lesson episodes (see Chikiwa & Graven, 2019)
Limitations of the study
A limitation of this research, especially in terms of the empirical contribution, is the small number of students in the sample, and the fact that the videos to which they responded in their reflections were of their own practice, while the facilitator-guided sessions featured the practice of other teachers. If the students had reflected on other teachers' practice after facilitator-guided sessions, the results may have been different, although we do not expect this to be the case. We did not at the time deem it feasible to ask PSTs to do additional written tasks as they were busy with other assignments and courses. Alternatively, had the facilitator-mediated sessions focused on videos of their own teaching, shifts towards increasing proportions of higher levels of reflections may have appeared. An additional limitation is that as time passed between the gathering of the data on the two sets of reflections one cannot claim that the shifts are a result of the facilitator-led session and not general experiences in their studies that might have supported strengthened RP. Furthermore, we did not qualitatively code differences in various reflections within the levels of description, explanation and suggestion other than to distinguish between those that were relatively simple and those that were expanded on and connected to further explanation (as shown in Table 3). Further differentiation and increased sensitivity in the coding of sub-levels per level may enable researchers to track progressions in PSTs' reflections that may not be visible in our coding system. Further research might usefully look at developing increased levels of refinement so that progress might be tracked within each of the levels of RP over time.
Concluding remarks
A contribution of the broader study is our adapting and developing a coding system for reflections in a way that might usefully reflect South African PST shifts in reflection. In our study the lecturer used Karsenty et al.'s (2015) SLF to support PSTs in looking at six different aspects of (looking through six different lenses at) lessons. The SLF however is not an analytic framework for researching qualitatively different levels of reflection. For our analysis of PSTs' reflection on lessons we thus looked at frameworks that delineated hierarchical levels of reflection. We argued in the article, with reference to our data, that the three-level frameworks of reflection of researchers in Australia and the corresponding indicators for identifying reflections at each of these levels were not sufficient for our purposes. In this article we used our adapted four-level analytic framework, along with a range of sub-categories for coding RP data to analyse the shifts in PSTs' RP. We found that PSTs, following small-group, facilitator-led sessions, provided many more suggestions. These however were at a basic level and without justification. They were thus not considered to meet the requirements of the highest level of reflection, that is, Reflectivity. We thus introduced Suggestion as a level between Explanation and Reflectivity and noted that the few instances (three) of Reflectivity that we found in ROP2 required consideration at the level of paragraph or at least a combination of L1, L2 and L3 ideas brought into combination with each other. Thus, while coding of ideas worked for L1, L2 and L3 reflections, and these ideas could be coded into a single category (thus avoiding ideas being coded into more than one category), this coding did not work for L4 as the definition itself involves bringing ideas into dialogue with one another.
Considering the limitations noted above, we have only tentative recommendations that build on the insights emerging from the study. The first is that, recognising the complexity and difficulty of developing RP, PTE needs to find ways to provide opportunities to model high levels of RP across multiple PST course offerings and opportunities for facilitator-led mediation of PSTs' observations and reflections. Tools such as the SLF (Karsenty et al., 2015) are useful for supporting PSTs in focusing on a range of aspects of lessons but are not sufficient to enable PSTs to reflect at higher levels. They also do not guarantee a focus on mathematical over general aspects of lessons. Pre-service teachers probably need much greater exposure to opportunities for developing RP across multiple contexts (e.g. live observation of lessons, viewing video recordings of the lessons of other teachers as well as their own) and multiple course offerings, from the first year of their studies. In this way, RP may come to offer powerful support for their future teaching as a sustainable dimension of their teaching practice.
Acknowledgements
This work is based on research supported by South African Research Chairs (SARCH) initiative of the department of Science and Technology and the National Research Foundations (Grant Number, 74658).
Competing interests
The authors declare that they have no financial or personal relationships that may have inappropriately influenced them in writing this article.
Authors' contributions
M.G. and S.C. collaborated on the published work. Both made a substantial contribution to conceptualisation and design, acquisition of data, analysis and interpretation of data, and drafting of the manuscript. M.G. further critically revised it for important intellectual content and approved the final version to be published.
Ethical considerations
Ethical clearance to conduct this study was obtained from the Rhodes University Faculty of Education Higher Degrees' Committee (no. 2017.12.08.06.)
Funding information
The authors acknowledge National Research Foundation (NRF) for funding this research.
Data availability
The data that support the findings of this study are available on request from the corresponding author, S.C.
Disclaimer
The views and opinions expressed in this article are those of the authors and do not necessarily reflect the official policy or position of any affiliated agency of the authors.
References
Abtahi, Y., Graven, M., & Lerman, S. (2017). Conceptualizing the more knowledgeable other within a multi-directional ZPD. Educational Studies in Mathematics, 96(3), 275-287. https://doi.org/10.1007/s10649-017-9768-1 [ Links ]
Askew, M., Bowie, L., & Venkat, H. (2019). Pre-service primary teachers' mathematical content knowledge: An exploratory study. African Journal of Research in Mathematics, Science and Technology Education, 23(3), 286-297. https://doi.org/10.1080/18117295.2019.1682777 [ Links ]
Ball, D.L., Thames, M.H., & Phelps, G. (2008). Content knowledge for teaching: What makes it special? Journal of Teacher Education, 59(5), 389-407. https://doi.org/10.1177/0022487108324554 [ Links ]
Beauchamp, G. (2006). New technologies and 'new teaching': A process of evolution. In R. Webb (Ed.), Changing teaching and learning in the primary school. Open University Press.
Cadiz, A.P. (2021). Pre-service teachers' reflective practice and their teaching practicum beliefs. Jurnal Inovatif Ilmu Pendidikan, 3(2), 105-119. [ Links ]
Centre for Development and Enterprise (CDE). (2013). Mathematics outcomes in South African schools, what are the facts? What should be done? Centre for Development and Enterprise.
Chen, H.T. (2016). Interfacing theories of program with theories of evaluation for advancing evaluation practice: Reductionism, systems thinking, and pragmatic synthesis. Evaluation and Program Planning, 59, 109-118. https://doi.org/10.1016/j.evalprogplan.2016.05.012 [ Links ]
Chikiwa, S. (2020). Exploring pre-service teachers' reflective practice in the context of video-based lesson analysis. Unpublished doctoral thesis. Rhodes University. [ Links ]
Chikiwa, S., & Graven, M. (2019). Using video-based mathematics lesson analysis to develop pre-service teachers' reflective practice. Mathematics Education Research Group of Australasia.
Chikiwa, S., & Graven, M. (2021). How pre-service teachers reflect on their own mathematics teaching practice compared to the practice of others. African Journal of Research in Mathematics, Science and Technology Education 25(2), 211-224. https://doi.org/10.1080/18117295.2021.1968164 [ Links ]
Chikiwa, S., & Graven, M. (2022, February). How the six-lens framework supports pre-service teachers' reflections. In 12th Congress of the European Society for Research in Mathematics Education (CERME12). Bozen-Bolzano, 2-6 February.
Cohen, S., Manion, L., & Morrison, K. (1972). Research methods in education (7th ed.). Routledge.
Creswell, J.W. (2014). A concise introduction to mixed methods research. Sage.
Darling-Hammond, L. (2009). Recognizing and enhancing teacher effectiveness. The International Journal of Educational and Psychological Assessment, 3, 1-24. [ Links ]
Dewey, J. (1933). How we think: A restatement of the relations of reflective thinking to the educative process. Heath and Company.
Farrell, T.S. (2015). Promoting teacher reflection in second language education: A framework for TESOL professionals. Routledge.
Fleisch, B. (2008). Primary education in crisis: Why South African school children underachieve in reading and mathematics. Juta & Co.
Genor, M. (2005). A social reconstructionist framework for reflection: The 'Problematizing' of teaching. Issues in Teacher Education, 14(2), 45-62. [ Links ]
Graven, M., & Lerman, S. (2014). Counting in threes: Lila's amazing discovery. For the Learning of Mathematics, 34(1), 29-31. [ Links ]
Hewitt, J., Pedretti, E., Bencze, L., Vaillancourt, B.D., & Yoon, S. (2003). New applications for multimedia cases: Promoting reflective practice in preservice teacher education. Journal of Technology and Teacher Education, 11(4), 483-500. [ Links ]
Hollingsworth, H., & Clarke, D. (2017). Video as a tool for focusing teacher self-reflection: Supporting and provoking teacher learning. Journal of Mathematics Teacher Education, 20(5), 457-475. https://doi.org/10.1007/s10857-017-9380-4 [ Links ]
Hutchinson, C.J., & Allen, K.W. (1997). The reflection integration model: A process for facilitating reflective learning. The Teacher Educator, 32(4), 226-234. https://doi.org/10.1080/08878739709555149 [ Links ]
Jay, J.K., & Johnson, K.L. (2002). Capturing complexity: A typology of reflective practice for teacher education. Teaching and Teacher Education, 18(1), 73-85. https://doi.org/10.1016/S0742-051X(01)00051-8 [ Links ]
Johns, C. (2010). Guided reflection: A narrative approach to advancing professional practice. Blackwell Publishing Ltd.
Karsenty, R. (2018). Professional development of mathematics teachers: Through the lens of the camera. In Invited lectures from the 13th international congress on mathematical education (pp. 269-288). Springer.
Karsenty, R., & Arcavi, A. (2017). Mathematics, lenses and videotapes: A framework and a language for developing reflective practices of teaching. Journal of Mathematics Teacher Education, 20(5), 433-455. https://doi.org/10.1007/s10857-017-9379-x [ Links ]
Karsenty, R., Arcavi, A, & Nurick, Y. (2015). Video-based peer discussions as sources for knowledge growth of secondary teachers. In K. Krainer, & N. Vondrova (Eds.), Proceedings of the 9th congress of the European society for research in mathematics education (pp. 2825-2832). CERME.
Karsenty, R., Pöhler, B., Schwarts, G., Prediger, S., & Arcavi, A. (2021). Processes of decision-making by mathematics PD facilitators: The role of resources, orientations, goals, and identities. Journal of Mathematics Teacher Education, 26, 1-25. https://doi.org/10.1007/s10857-021-09518-z [ Links ]
Kullman, J. (1998). Mentoring and the development of reflective practice: Concepts and context. System, 26(4), 471-484. https://doi.org/10.1016/S0346-251X(98)00033-5 [ Links ]
Lee, H.J. (2005). Understanding and assessing pre-service teachers' reflective thinking. Teaching and Teacher Education, 21(6), 699-715. https://doi.org/10.1016/j.tate.2005.05.007 [ Links ]
Liou, H.C. (2001). Reflective practice in a pre-service teacher education program for high school English teachers in Taiwan, ROC. System, 29(2), 197-208. https://doi.org/10.1016/S0346-251X(01)00011-2 [ Links ]
Mewborn, D.S. (1999). Reflective thinking among preservice elementary mathematics teachers. Journal for Research in Mathematics Education, 30(3), 316-341. https://doi.org/10.2307/749838 [ Links ]
Muir, T., & Beswick, K. (2007). Stimulating reflection on practice: Using the supportive classroom reflection process. Mathematics Teacher Education and Development, 8, 74-93. [ Links ]
Norrie, C., Hammond, J., D'Avray, L., Collington, V., & Fook, J. (2012). Doing it differently? A review of literature on teaching reflective practice across health and social care professions. Reflective Practice, 13(4), 565-578. https://doi.org/10.1080/14623943.2012.670628 [ Links ]
Olteanu, C. (2017). Reflection-for-action and the choice or design of examples in the teaching of mathematics. Mathematics Education Research Journal, 29, 349-367. https://doi.org/10.1007/s13394-017-0211-9 [ Links ]
Reddy, V., Visser, M., Winnaar, L., Arends, F., Juan, A.L., Prinsloo, C., & Isdale, K. (2016). TIMSS 2015: Highlights of mathematics and science achievement of Grade 9 South African learners. Human Sciences Research Council.
Reddy, V., Winnaar, L., Arends, F., Juan, A., Harvey, J., Hannan, S., & Isdale, K. (2022). The South African TIMSS 2019 Grade 9 results: Building achievement and bridging achievement gaps. Human Sciences Research Council.
Roberts, N. (2020). Maths intensive: First design trial in response to printed mathematics assessment. In P. Vale, L. Westaway, Z. Nhase, & I. Schudel (Eds.), Proceedings of the 28th annual conference of the Southern African Association for Research in Mathematics, Science and Technology Education (pp. 126-142). SAARMSTE.
Russell, T. (2005). Can reflective practice be taught? Reflective practice. International and Multidisciplinary Perspectives, 6(2), 199-204. https://doi.org/10.1080/14623940500105833 [ Links ]
Schon, D. (1983). The reflective practitioner: How professionals think in action. Basic Books.
Schwarts, G., & Karsenty, R. (2020). Can this happen only in Japan?: Mathematics teachers reflect on a videotaped lesson in a cross-cultural context. Journal of Mathematics Teacher Education, 23, 527-554. https://doi.org/10.1007/s10857-019-09438-z [ Links ]
Selmo, L., & Orsenigo, J. (2014). Learning and sharing through reflective practice in teacher education in Italy. Procedia-Social and Behavioral Sciences, 116, 1925-1929. https://doi.org/10.1016/j.sbspro.2014.01.496 [ Links ]
Shoffner, M. (2009). The place of the personal: Exploring the affective domain through reflection in teacher preparation. Teaching and Teacher Education, 25(6), 783-789. https://doi.org/10.1016/j.tate.2008.11.012 [ Links ]
Shulman, L.S. (1987). Knowledge and teaching: Foundations of the new reform. Harvard Educational Review, 57(1), 1-23. [ Links ]
Spaull, N., & Kotze, J. (2015). Starting behind and staying behind in South Africa: The case of insurmountable learning deficits in mathematics. International Journal of Educational Development, 41, 13-24. https://doi.org/10.1016/j.ijedudev.2015.01.002 [ Links ]
Stemler, S.E. (2015). Content analysis. Emerging trends in the social and behavioral sciences: An Interdisciplinary, searchable, and linkable resource (pp. 1-14). John Wiley & Sons, Inc.
Venkat, H., & Spaull, N. (2014). What do we know about primary teachers' mathematical content knowledge in South Africa? An analysis of SACMEQ 2007. Working Papers 13/2014. Stellenbosch University, Department of Economics.
Vygotsky, L.S. (1978). Mind in society: The development of higher psychological process. Harvard University Press.
Ward, J., & McCotter, S. (2004). Reflections a visible outcome for preservice teachers. Teaching and Teacher Education, 20(3), 243-257. https://doi.org/10.1016/j.tate.2004.02.004 [ Links ]
Zeichner, K.M. (1994). Research on teacher thinking and different views of reflective practice in teaching and teacher education. Teachers' minds and actions: Research on teachers' thinking and practice (pp. 9-27). Routledge.
Ziegler, G.M., & Loos, A. (2017). "What is Mathematics?" and why we should ask, where one should experience and learn that, and how to teach it. In Proceedings of the 13th International Congress on Mathematical Education: ICME-13 (pp. 63-77). Springer International Publishing.
 Correspondence:
Correspondence:
Samukeliso Chikiwa
s.chikiwa@ru.ac.za
Received: 31 Jan. 2022
Accepted: 14 Apr. 2023
Published: 28 June 2023
1. In identifying the event as a shortfall, she is implicitly suggesting she needs to improve the way she instructs learners.














