Services on Demand
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
Pythagoras
On-line version ISSN 2223-7895
Print version ISSN 1012-2346
Pythagoras vol.44 n.1 Cape Town 2023
http://dx.doi.org/10.4102/pythagoras.v44i1.711
ORIGINAL RESEARCH
Talk that supports learners' folding back for growth in understanding geometry
Kabelo ChueneI; Koena MabotjaII; Satsope MaotoI
IDepartment of Mathematics, Science and Technology Education, Faculty of Humanities, University of Limpopo, Polokwane, South Africa
IIDepartment Natural Sciences Teaching, Mathematics Education, Faculty of Humanities, Sol Plaatje University, Kimberley, South Africa
ABSTRACT
In this article, we argue that folding back is successful when the learners engage in exploratory talk. To support our argument, we sourced data from a Grade 10 mathematics classroom of 54 learners who participated in a four-week teaching experiment conducted by the second author. We mainly focused on talks in two groups of learners to address the silence of literature on folding back that alludes to the kind of talk that learners engage in. Data were captured through video recording of learners' interactions as they worked on the tasks in different sessions. We present these data as transcribed extracts of talks that the learners held and synthesise them into stories through Polkinghorne's narrative mode of data analysis, also using a process that Kim referred to as narrative smoothing. Pirie and Kieren's conception of folding back and Wegerif and Mercer's three ways of talking and thinking among learners were used as a heuristic device for synthesising the stories. The narratives illustrate that exploratory talk promotes folding back, where learners build on each other's ideas to develop geometry understanding. Therefore, the significance of this article is that for classrooms that wish to promote growth in understanding through folding back, the type of talk that should be normative is exploratory talk.
CONTRIBUTION: Our search of the literature databases has yet to reveal an empirical study that draws attention to exploratory talk's role in developing learners' understanding of geometry in South Africa. However, this study is one of those that allude to the support of exploratory talk on folding back in developing geometry understanding. Our findings imply that mathematics classrooms should consider incorporating exploratory talk as part of teaching and learning geometry. Furthermore, studies on engendering exploratory talk in teaching mathematics are recommended
Keywords: folding back, dynamical theory of the growth of mathematical understanding, dialogical framework for researching peer talk, geometry understanding
Introduction
The study of high school geometry remains a challenge in mathematics education. However, some studies show that folding back in Pirie and Kieren's theory of growth in mathematical understanding is beneficial for growth in geometry understanding. For example, when Gülkilik et al. (2015) examined Grade 10 learners' understanding of geometric transformation, they recommended that learners should be encouraged to fold back to the inner levels to strengthen how concepts are understood. In addition, Pirie and Kieren's theory enabled Yao (2020) to capture the evolving understanding of geometric transformation when working with secondary school preservice teachers. Also, a study by Akarsu (2022) showed that the theory, when used together with Van Hiele's model of geometric thinking, offers a unique perspective for appreciating how learners develop an understanding of geometric reflection. While framing their study on Piere and Kieren's theory jointly with Duval's (2006) Semiotic Representation Theory, Gülkılık et al. (2020) asserted that the former theory enabled the construction of images about geometric concepts as well as noticing mathematically significant and traceable properties of that concept. However, while some researchers have used Pirie and Kieren's theory and its extension by Martin (2008) to track and trace learners' understandings (Yao, 2021), there seems to be no study that examined the kind of talk that takes place during these processes.
Yao and Manouchehri (2022) argue that work that focuses on learners' growth of geometry understanding is still scarce. They further claim that how folding back might occur is not yet clear. Factors that enhance folding back towards developing specific mathematical actions are not explicit. For example, Chiphambo and Feza (2020) conducted a study with Grade 8 learners and found that teaching methods influenced how to succeed in geometry. The specific methods mentioned are the hands-on and mind-on learning of geometric concepts. However, studies on folding back and focusing on learners' understanding of geometry do not analyse the type of talk learners engage in so that understanding can occur. This silence in the literature occurs regardless of acknowledgements of enhanced cognitive activity that come with talk interventions in classrooms (Soysal, 2019). Though Yao and Manouchehri (2022) detailed how folding back takes place, they also did not classify the type of talk that the learners use. Therefore, in a context where folding back offers learners a way of deepening learning through visiting earlier forms of understanding (Hähkiöniemi et al., 2023) to build deeper mathematical understanding and language (Corovic, 2022), this article argues that folding back is successful when the learners engage in exploratory talk. Potentially, 'exploratory talk provides the richest and most valuable contribution to the quality of learning' (Chan, 2020, p. 10). In a South African study by Hardman and Lilley (2023), exploratory talk among learners symptomised a 'truly dialogical interaction, where partners together construct meaningful [mathematics] knowledge through negotiation and debate'. (p. 13).
In mathematics, Sfard (2008) brought to the fore the relationship between thinking and speech in her theory on commognition, a term she coined to combine thinking with communication. Mercer (2008) has also drawn a correlation between talking, reasoning and understanding in education. He classified such talk into three types: disputational, cumulative, and exploratory (2008). Disputational talk is observable when there are no agreements and individualised decision-making. In cumulative talk, learners construct knowledge common among themselves through repetition, confirmation and elaborations. In exploratory talk, 'partners engage critically but constructively with each other's ideas' (Mercer & Littleton, 2007, p. 72). For example, a Flemish study conducted by T'Sas (2018) found that when exploratory talk is taught properly, the learners learn from each other to improve group reasoning. This was not the only benefit; the learners improved skills on argumentation and problem-solving. A South African study conducted in a Physical Science classroom showed that learners used exploratory talk when working on tasks requiring application (Radebe & Mushayikwa, 2023). In addition to the benefits of exploratory talk in classrooms, it encouraged the development of critical thinking, the elements of which were in expressing differing views and offering clear justifications (Liang & Fung, 2021). These benefits can be extended to mathematics learners as evidenced in a South African study by Webb et al. (2017). Furthermore, '[i]n [exploratory] talk, all partners actively participate, opinions are sought, and decisions are jointly made' (Røsseland et al., 2022, p. 1). However, the occurrence of exploratory talk in folding back as a process through which understanding develops has not been captured in literature. In this study, the following research question was addressed: What kind of talk is necessary for folding back to help learners develop geometry understanding?
Theoretical framework
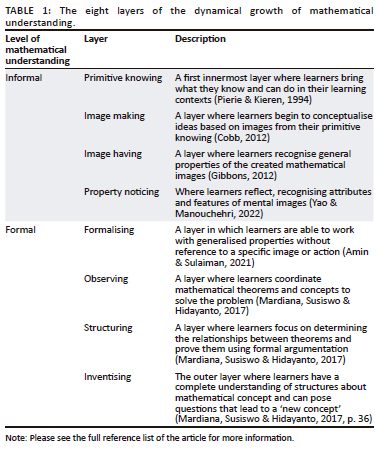
To analyse learners' growth in understanding geometry, we adapted Pirie and Kieren's (1994) dynamical theory of the growth of mathematical understanding. This theory contains eight nested layers that explain the non-linear process of learning mathematics. Table 1 lists these layers and their descriptions.
Pirie and Kieren's (1994) theory has a vital characteristic called folding back. Through folding back, learners reconstruct and elaborate on an inner level of understanding to support the next level of understanding. Learners use folding back when they fail to apply their understanding at a specific level. Instead, they move back to an inner level to extend their understanding and reorganise it so that they can address their failure (Gülkılık et al., 2015). Martin (2008) argued that the notion of folding back was initially underdeveloped and unelaborated. Subsequently, he proposed a framework that elaborated on folding back as having three tenets. The three tenets are the source of intervention, the form of folding back and the outcome of folding back. In this article, folding back is a lens through which we explored how learners build on each other's ideas to develop their understanding of geometry.
The source of intervention invokes a learner to fold back. The source of intervention may be the self, a peer, a teacher or material at a learner's disposal (Martin, 2008). According to Martin (2008), the form of folding back describes actions that learners engage in because of the source of intervention. These actions may involve working at an inner layer using existing understanding, collecting at an inner layer, moving out of topic, working there, and causing a discontinuity. The actions that make up the forms of folding back may result in either effective or ineffective folding back. Effective folding back occurs when learners apply a comprehensive understanding to solve the initial problem (Martin, 2008). Contrary to that, ineffective folding happens when learners cannot apply comprehensive understanding to the initial problem.
Furthermore, we had to analyse how learners build on each other's ideas as peers. We found Wegerif and Mercer's (1997) dialogical framework for researching peer talk in which they define social modes of thinking through three kinds of talk relevant for our analysis. Wegerif and Mercer's perspective on talk as a thinking tool enabled them to delineate thinking that is 'embodied in different types of talk' (p. 60). They found these kinds of talk appropriate to explain how to use talk to build on each other's ideas. These talks are disputational talk, cumulative talk and exploratory talk (Wegerif & Mercer, 1997). In disputational talk, participants tend to be defensive in justifying their contribution to the talk because others may view their ideas narrowly (Mercer, 2008). Mercer (2008) characterises cumulative talk as repetitions, confirmations and elaborations that avoid differing opinions to maintain the image of a group. However, the partners offer statements and suggestions to consider jointly in exploratory talk (Wegerif & Mercer, 1997). They may challenge and counter-challenge suggestions, but challenges are justified, and they can offer alternative hypotheses. All partners participate actively, and opinions are sought and considered before making joint decisions. 'Compared with the other two types of talk, in exploratory talk is more publicly accountable and reasoning is more visible in the talk' (Mercer & Wegerif, 2004, p. 87). Furthermore, exploratory talk fosters critical thinking and cognitive development (Mercer, 1996). Although not an exhaustive list, the following features were identified by Mercer (2008) to characterise exploratory talk:
-
Everyone is encouraged to contribute.
-
Everyone listens actively.
-
People ask questions.
-
People share relevant information.
-
Ideas and opinions are treated with respect.
-
There is an atmosphere of trust.
-
There is a sense of shared purpose.
-
Contributions build on what has gone before.
-
People give reasons for their thinking.
-
Ideas may be challenged.
-
The group seeks agreement for joint decisions.
The three types of talk are 'not meant to be descriptive categories into which all observed speech can be neatly and separately coded' (Wegerif & Mercer, 1997, p. 54). Both the Pirie and Kieren (1994) dynamical theory of the growth of mathematical understanding and Wegerif and Mercer's (1997) dialogical framework for researching peer talk are not meant to chunk data into fixed categories but will be used to explicate the data and illustrate that exploratory talk is essential for folding back to occur.
Methods
We sourced data from a Grade 10 mathematics classroom of 54 learners who participated in a four-week teaching experiment conducted by the second author. This article mainly focuses on talks in two groups of learners. Teaching experiments are a sequence of teaching episodes through which the researchers study and theorise about learners' learning and reasoning in mathematics (Lamb & Geiger, 2012). In addition, teaching experiments offer researchers opportunities to learn the mathematical knowledge of learners and how they construct it through talk (Steffe & Thompson, 2000). Through teaching experiments, researchers can systematically investigate the development of learners' meaning (Moore et al., 2019). Hence, the teaching experiment allowed us to identify critical incidents where learners' exploratory talk allowed them to fold back to grow their understanding as they worked through some geometry tasks. We did not expect these incidents to happen, but they have 'the potential to deepen our understanding of learners' [growth in mathematical understanding]' (Choy, 2014, p. 143). The incidents we analysed for this study came from two groups of learners out of 54 Grade 10 mathematics learners. In the first group, the participants' pseudonyms were John and Koena; in the second group, they were Lesiba, Lebogang and Sipho. The sample size of these two groups is consistent with the teaching experiment research design as it allows one ora few learners as participants in the study (Steffe & Thompson, 2000).
Data were captured through video recordings of learners' interactions as they worked on the tasks in different sessions. We present data as extracts of transcripts of talks that the learners held because talk is used to check learners' growth in understanding. We synthesised the extracts into stories through the narrative mode of data analysis (Polkinghorne, 1995). This mode of data analysis allowed us to fill gaps in narratives and bring meaning that was not necessarily explicit in the extract. Kim (2016) refers to this process of filling gaps in data as narrative smoothing. Narrative smoothing helps make narratives coherent and engaging. In narrating the extracts, the frameworks by Pirie and Kieren's (1994) conception of folding back, Martin's (2008) elaboration of folding back and Wegerif and Mercer's (1997) three ways of talking and thinking among learners were used as a heuristic device for synthesising the talks. We chose the extracts of talk where understanding of geometric ideas can be explained through folding back to illustrate instances of exploratory talk.
Quality criteria
Teaching experiments are judged on their ability to provide a model or argument related to teaching and learning because they are grounds for researchers to learn (Molina et al., 2007). Hence, this article argues that folding back is successful when the learners engage in exploratory talk. The argument is not limited to one extract but to two and is new to studies on folding back, as shown in the introduction of the article. However, the argument cannot be replicated in other settings as this is not a requirement for teaching experiments (Steffe & Thompson, 2000). Instead, it can be transferred to other settings for progressive refinement of the argument by either the authors of this article or other researchers interested in folding back. Retrospective analysis of the data for this article was made possible by capturing data on video to enable both the first author and the other authors to recollect what happened during data collection.
Ethical considerations
The second author applied for ethical clearance to conduct the study through the university's ethical committee, the school's principal, and the parents of participating learners. Ethical clearance to conduct this study was obtained from the University of Limpopo, Turfloop Research Ethics Committee (Clearance Certificate no. TREC/51/2016:PG). He also informed the learners who willingly participated in data construction without compensation for the study. As participants, the learners had a chance to enrich their knowledge of geometry as the study stayed within the prescribed curriculum.
Results
The analysis presented here illustrates instances of talks where the process of folding back happened as learners engaged in exploratory talk as they worked on two geometry learning tasks.
The first task assessed learners' ability to apply the theorem that states that an exterior angle of a triangle is equal to the sum of its two opposite non-adjacent interior angles. The task (Figure 1) was stated as follows. If ∠ A = 90°, prove that DÔC = 45°.
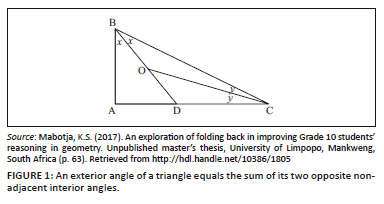
Using layers of understanding by Pirie and Kieren (1994) as a referent, the assessment task was pitched at the property noticing level. Learners had to notice that they had to apply properties of exterior angles of a triangle and the sum of angles in a right-angled triangle. The following extract starts after John asked the class teacher for help:
1.1.
John:
Sir, please help us to find DÔC.
1.2.
Teacher:
What will be the sum of ∠ B?
1.3.
John:
2x … hmmmm ∠ B1 is equal to ∠ B2 and ∠ B2 is equal to x, which means each of ∠ B1 and ∠ B2 is x, do you understand?
1.4.
Koena:
Eish … [shaking head-indicating that he does not understand].
1.5.
John:
It means that here [pointing at ∠ B and ∠ C] it is 2x and 2y …
1.6.
Koena:
Oh, I understand now, meaning ∠ B is having two angles …
The teacher intervened by asking a question that looked for the sum of the angles that formed ∠ B. John's answer suggested that he understood the representation of these angles and then showed that they are equal. Hence, he gave the sum of the angles to be 2x. In this instance, the teacher's intervention was explicit and intentional as it led John to the desired response. In a similar manner, John realised that ∠ C = 2 y. In so doing John was able to fold back from the property noticing level to the image having level. John then checked with Koena if he shared his understanding; this comparison is one of the indicators of exploratory talk.
However, Koena's reaction on line 1.4 suggested that he did not understand. John drew Koena's attention to notice that ∠ B and ∠ C were sums of 2x and 2y. This part of exploratory talk led Koena to move from primitive knowing to image having. As observed by Mercer et al. (1999, p. 97), 'in exploratory talk, knowledge is made publicly accountable and reasoning is visible in the talk'.
When John shared his ideas with Koena, the ideas contributed to Koena's development of geometry ideas. Koena was observed building on John's ideas and reformulating them as: '∠ B is having two angles …' (line 1.6). Folding back by both John and Koena (moving from image having level to property noticing) resulted in an environment where the two learners could develop an idea together. In this instance, we observed John's exploratory talk characterised by mathematical actions such as explaining and justifying ideas to his peer. Thus, learners' ability to explain their own ideas become enhanced when they engage in exploratory talk.
The talk between John and Koena continued in the extract that follows. It began with John questioning how they can evaluate ∠ x and ∠ y. This makes the teacher the source of the intervention. Again his intervention was intentional and explicit because it ultimately led the learners to the size of ∠ x and ∠ y:
1.7.
John:
Yes … question is, how are we going to calculate 𝑥 and 𝑦?
1.8.
Teacher:
What will be the sum of angles in that triangle?
1.9.
John:
90° + 2x + 2y = 180° [talking and writing]
1.10.
John:
90° + 2x + 2y = 180° … 2x + 2y = 90°
1.11.
Koena:
So, do we find x first?
1.12.
John:
What if we divide by 2?
1.13.
Koena:
We divide 2x + 2y by 2 … then we remain with x + y = 45°
In this extract, it can be claimed that when John asked the question on how to calculate the sizes of x and y, he trusted that the group members would share relevant information. In sharing the responsibility of working out the problem, the teacher asked them about the sum of angles of a triangle. The teacher's questioning guided learners to knowledge that they had met before. Hence, the response by John, who talked as he wrote: 90° + 2x + 2y = 180°. In so doing, the teacher invoked John to collect knowledge at an inner level. In this case, John's mathematical actions suggested that he noticed the properties of the sum of angles in a triangle. These actions were evidence that he was at a property noticing level. The talk proceeded with Koena and suggested that they solve for x first. Instead, John suggested that they divide by 2. Koena proceeded to divide the terms of the equation by 2 to get x + y = 45°. This move indicated that there was no competition of ideas in the group. Instead, there was a sense of shared purpose.
The next extract shows the interactions between learners when they finalised their work on the task. The extract began with an intervention from John. He suggested that the other learners should rotate the drawing and redraw it (Figure 2):
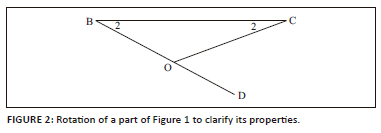
1.14.
John:
Let us say we put it this way [rotate the learning activity drawing] … draw it [suggest that other peers draw].
1.15.
Sipho:
How?
1.16.
John:
Looking at it the way it is …
1.17.
Sipho:
I am going to make mistake.
1.18.
John:
[Starts drawing] [see Figure 2]
1.19.
Koena:
Ohoo ∠ 0 is an exterior angle.
1.20.
John:
Yes, my friend … so ∠ 0 is equal to B2 + C2 (exterior) … ohooo … wooowwww! ∠ 0 is equal to ∠ B, ∠ B is the same as, look at it x + y; ∠ 0 = x + y … ∠ 0 = 45°.
The talk started with John encouraging the group members to redraw the diagram after he rotated it. It seems that John wanted to rotate the diagram so that it became easier to identify properties of the diagram that would help them solve the problem at hand. The dynamical theory of the growth of mathematical understanding refers to this as the property noticing layer. He drew the learners' attention to the triangle BOC where the angle BÔC is located. The learners had to move out of the idea that was required on the task to transformation of the diagram. Immediately, John drew the diagram that isolated the required and sufficient information to finalise the proof. Koena was able to notice that DÔC is an exterior angle to. Δ BOC. John extended this observation to conclude that DÔC equals x + y = 45°. In the extract John referred to angles x and y as B2 and C2.
John's utterances showed that he was impressed by the observation by Koena. He said 'exterior … ohooo … wooowwww!'. This utterance can be classified as a characteristic of exploratory talk where learners treat each other's ideas and opinions with respect and appreciation. Again it can be argued that through folding back, an environment in which learning results from co-construction of ideas and extension of these ideas is able to flourish.
After the class was taught about the midpoint theorem, the learners were assessed using the task below. Using the framework for growth of mathematical understanding (Pirie & Kieren, 1994) as referent, the learning activity was considered to be at the formalising layer. In this learning activity, learners were required to consciously notice properties related to the midpoint theorem and use them to calculate the interior angles of Δ MNT. Thus, the learning task required learners to reason with properties of the objects (Gibbons, 2012; Wright, 2014).
In Figure 3, the points M, N and T are the midpoints of sides AB, BC, and AC respectively in Δ ABC. Calculate the interior angles of Δ MNT.
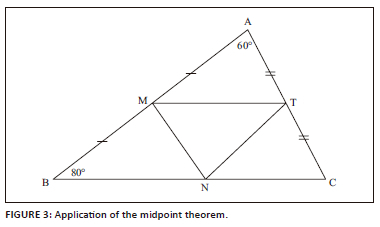
The learners seemed to notice that they could use the idea that the sum of angles in a triangle are equal to 180°. They were observed calculating the magnitude of ∠ C. They also determined the magnitude of the other angles in the diagram before evaluating the interior angles of Δ MNT. Once they finished, they studied the diagram in silence until Sipho asked, 'So how do we find angles M, N and T?' The extract that follows represents the interactions that emerged:
2.1.
Sipho:
How do we determine angles M, N and T?
2.2.
Lesiba:
Is it not possible to use midpoint theorem?
2.3.
Sipho:
Isn't this F? This is F … you see …
2.4.
Lebogang:
Then it is corresponding angles …
2.5.
Lesiba:
Of parallel lines.
2.6.
Lebogang:
It means that here [pointing to ∠ N], we are going to represent it as ∠ N1, ∠ N2 [TN̂C], here [pointing to ∠ T] ∠ T1 and ∠ T2.
2.7.
Lesiba:
But here they didn't give us ∠ N1 and ∠ N2. [Inaudible] ∠ of ∆ MTN and then midpoint of AC is T … midpoint MN and TR are midpoints of …
2.8.
Lebogang:
If we can say ∠ N1 and ∠ N2 we will understand that ∠B is equal to ∠ N2, then they are corresponding.
2.9.
Sipho:
Ohoo … understand, these are the angles that Lebogang is talking about, this is F…
2.10.
Lesiba:
I can see that …
2.11.
Lebogang:
This means ∠ N2 is equal to 80°.
2.12.
Sipho:
Wait a minute! Oh yes I can see that.
2.13.
Lebogang:
Then here it's ∆ TNC.
2.14.
Sipho:
Hmmm.
2.15.
Lesiba:
Hmmm.
2.16.
Sipho:
You are using a long way … Ohooo yes continue …
2.17.
Lebogang:
Then in ∆ TNC, we are going to do just like the first part, we take ∠ N2 and add it with ∠ N then subtract from 180° to get ∠ T2 [NT̂C].
2.18.
Sipho:
Hmmm I see it.
2.19.
Lesiba:
We are supposed to find ∠ M, ∠ N and ∠ T.
2.20.
Lebogang:
Wait, listen, ∠ N2 is alternating to ∠ T1.
2.21.
Sipho:
Show [Pause] Yes, carry on Lebogang.
2.22.
Lebogang:
[starts writing]
2.23.
Sipho:
So ∠ T1 is 80°.
2.24.
Lesiba:
Alternating angles are equal …
2.25.
Lebogang:
Alternating angles are equal. It means that ∠ T1 is 80°.
The extract began with Sipho asking the group members how to get the size of the angles in triangle MTN. Lesiba suggested that they use the midpoint theorem, an indication that he was operating at the image making level. Pointing at TN̂C and MB̂N, Sipho examined the diagram and said that it satisfies the properties for F, a mnemonic that is used for corresponding angles that are formed from parallel lines. Even though the learners did not give a mathematically justifiable reason, this suggests that he was aware that line BM is parallel to line NT. The group followed on this train of thought by providing more relevant information and identified that TN̂C and MB̂N are corresponding angles formed by parallel lines. This exploratory talk assisted Lebogang to engage in acts of property noticing; she noticed that each of angles ∠ N and ∠ T consisted of three angles. She named them ∠ N1, ∠ N2, ∠ N3, and ∠ T1, ∠ T2, ∠ T (see Figure 4).
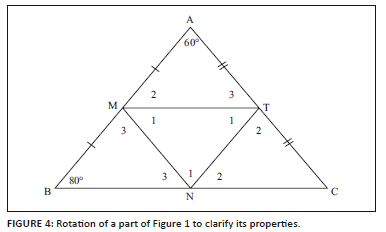
This further confirms Rojas-Drummond et al.'s (2013) and Mercer and Wegerif's (2004) assertions that reasoning is visible in exploratory talk.
It seemed Lesiba did not understand Lebogang's workings because he did not notice how that related with the midpoint theorem. But once he realised that she did this to show that TN̂C = ∠ B = 80° where TN̂C = ∠ N2 he accepted what Lebogang did. In this instance, there is evidence of exploratory talk which resulted in explicit peer intentional intervention, as observed where both Lebogang and Lesiba developed an understanding of the ideas used towards solving the given activity. Thus, through exploratory talk, Lesiba appeared to be actively involved in the resolution of the learning activity as he could share his ideas concerning the learning activity. Furthermore, Lesiba's utterances in lines 2.7 and 2.10 highlight instances where 'opinions are sought and considered before decisions are jointly made' (Mercer & Wegerif, 2004, p. 72) during exploratory talk.
It is also evident in the vignette that through exploratory talk learners had different ways of working on a mathematics task. In this extract, although Sipho perceived that Lebogang used a lengthy method to solve the problem, immediately after Sipho's utterance, it seems he realised the knowledge that Lebogang used towards solving the problem; he said: 'Ohooo yes, continue'. This affirms Barnes's (2010) concession that exploratory talk offers alternative ways of thinking about a task, which account for valued contributions in the learning environment (Chan, 2020). The utterance indicates that although Sipho almost challenged what Lebogang did, he was attentive. In this instance, we claim that Sipho developed an understanding of the approach used by Lebogang. Hence, Sipho's utterance in line 2.16 shows that what happened was now shared. Lebogang proceeded to show that NT̂C is computed by subtracting the sum of ∠ C and TN̂C from 180°. Exploratory talk eased the learners to accept challenging ideas presented by their peers. This ease aligns itself with a characteristic of exploratory talk, where learners' ideas become challenged in a learning environment (Dahl et al., 2018; Mercer & Wegerif, 2004).
Although learners were able to compute the magnitude of other angles such as NT̂C with appropriate geometry reasoning, Lesiba made them aware that the computation did not solve the given problem because they were supposed to calculate the interior angles of Δ MNT. In this case folding back caused a discontinuity. It can be claimed that in this group the learners felt at ease with challenging ideas that are presented by others.
Lesiba's exploratory talk resulted in learners folding back from property noticing to the formalising layer where they applied properties of various angles to determine the interior of angles of Δ MNT, as follows:
2.26.
Lebogang:
Wait, listen, ∠ N2 is alternating to ∠ T1.
2.27.
Sipho:
Show [Pause] Yes, carry on Lebogang.
2.28.
Lebogang:
[starts writing] ∠ T1 = ∠ N2.
2.29.
Sipho:
So ∠ T1 is 80°.
2.30.
Lesiba:
Alternating angles are equal …
2.31.
Lebogang:
Alternating angles are equal. It means that ∠ T1 is 80°.
2.32.
Lesiba:
Ohoo so ∠ T1 is the angle inside Δ MNT. Here [pointing at ∠ M1] is equal to ∠ T3.
2.33.
Lebogang:
Yes Lesiba, here we can see that ∠ T3 is 40° because it is corresponding with ∠C.
2.34.
Sipho:
So then ∠ M1 is equal to 40°, these [∠ T3 and ∠ M1] are alternating angles.
2.35.
Lesiba:
Yes.
2.36.
Lebogang:
Then we can use the sum of angles in Δ MNT to find ∠ N1.
2.37.
Sipho:
Yes, let's write it.
2.38.
Lesiba:
Okay I see it, ∠ T1 plus ∠ M1 plus ∠ N1 is 180°.
2.39.
Sipho:
Sum of angles in a triangle.
2.40.
Lebogang:
[starts writing] ∠ T1+ ∠ M1 + ∠ N1 = 180° (Sum of ∠s in triangle).
2.41.
Lesiba:
Let us substitute the values of the other two angles.
2.42.
Lebogang:
[continues writing] ∠ N1 = 180° - 40° - 80°.
2.43.
Sipho:
Yes, so ∠ N1 = 60°.
The above extracts illustrated that Lebogang successfully demonstrated how ∠ T of Δ MNT is calculated, evidence that she consciously noticed properties of alternating angles and worked with them. In addition, Sipho added by giving the size of ∠ T and Lesiba justified why what they did is geometrically accurate - an indication that everyone can contribute during exploratory talk of problem-solving. Eventually the learners were able to fold back to the formalising level where they determined the magnitude of the angles of Δ MNT.
Conclusion and recommendations
This article argues that folding back is successful when the learners engage in exploratory talk. We supported this argument by providing extracts of talk among groups of learners. These talks showed that learners could fold back as they worked on the given problems because they (1) allowed individuals to take the lead in the talk, (2) followed up on ideas presented in the group, and (3) either supported or challenged ideas in an uncompetitive way.
In the article, we pursued the question: What kind of talk is necessary for folding back to help learners develop geometry understanding? We used the narrative mode of data analysis to analyse the type of talk learners engage in while folding back (Martin, 2008). Two groups of learners were video recorded while working on geometry learning activities and our focus was on the learners' instances that promoted the building of ideas through folding back. The article shows that exploratory talk promotes folding back where learners build on each other's ideas to develop geometry understanding. As learners moved across different layers of understanding, they shared their thought processes which helped their peers to enhance their geometry understanding (Extract 1 and Extract 2). Banes et al. (2020) claimed that exploratory talk in mathematics classrooms is rare. Therefore, this claim necessitates studies that explore engendering exploratory talk in teaching and learning of geometry in schools. Furthermore, we encourage research to examine the understanding of geometry concepts using Pirie and Kieren's (1994) conception of folding back and Wegerif and Mercer's (2004) three ways of talking and thinking.
This finding concurs with Towers and Martin's (2014) study, which attests that individual learners' actions and statements contribute towards building understanding for a group of learners. In addition, the finding may be comparable to Hunter and Civil's (2021, p. 16) observation of learners who participate in collaborative groups, not as singles but 'as an interrelated and interdependent organism'. The finding was evident when learners explained and elaborated their actions, such as using mnemonics to solve the geometry learning activities. For Wei and Ismail (2010) and Martin and Towers (2015), this leads to a pathway for learners to modify and build their mathematical understanding. Through folding back, learners become interested not only in their geometry understanding but also in their peers' understanding. This results in an opportunity for peers to explain their preferred approach in solving geometry learning activities.
Furthermore, folding back promotes an environment where ideas are not only shared but appreciated. Through folding back, individual learners respect and encourage their peers to apply and articulate preferred methods to arrive at the solution of a geometry learning activity. Learners' ability to articulate their actions in resolving geometry learning activities not only promotes their confidence but plays a significant role in their development of geometry understanding (Mabotja, 2017; Yao & Manouchehri, 2022). As a result, learners become collaborative instead of competitive in their geometry learning environment. Our overall reflection on the cited narratives prompts us to conclude that for teachers who wish to promote growth in understanding through folding back, the type of talk that should be normative is exploratory talk. Teachers should request learners to explain, evaluate, and argue, while trading off merely finding answers for classroom talk that emphasises reasoning (Røsseland et al., 2022).
Acknowledgements
This article is partially based on the author's thesis entitled 'An exploration of folding back in improving Grade 10 students' reasoning in geometry' toward the degree of Master of Education in the Department of Mathematic, Science and Technology Education, University of Limpopo, South Africa, with supervisor(s) Prof. K.M. Chuene and Prof. R.S. Maoto, received 2017, it is available here: http://hdl.handle.net/10386/1805.
Competing interests
S.M. is an editorial board member of Pythagoras journal. The authors declare that they have no financial or personal relationships that may have inappropriately influenced them in writing this article.
Authors' contributions
K.M. produced the draft article from his master's study which was supervised by K.C. K.C. re-conceptualised the article by revising the argument and introducing a framework for analysing the kind of talks. S.M. improved the readability of the article, ensured alignment and worked particularly on improving the abstract and conclusion sections. All authors reviewed the article, assigned each other roles to improve the article for final submission and finally K.C. prepared the article for submission.
Funding information
This research received no specific grant from any funding agency in the public, commercial or not-for-profit sectors.
Data availability
Data used in the article were extracted from K.M.'s master's dissertation and can be requested.
Disclaimer
The views and opinions expressed in this article are those of the authors and do not reflect the official policy or position of any affiliated agency of the authors.
References
Amin, S.M., & Sulaiman, R. (2021). Students' growing understanding in solving mathematics problems based on gender: Elaborating folding back. Journal on Mathematics Education, 12(3), 507-530. https://doi.org/10.22342/jme.12.3.14267.507-530 [ Links ]
Akarsu, M. (2022). How the van Hiele theory and the Pirie-Kieren theory can be used to assess PT's understanding of concept of reflection. EKEV Akademi Dergisi, 90, 363-376. [ Links ]
Banes, L.C., Restani, R.M., Ambrose, R.C., Martin, H.A., & Bayley, R. (2020). Relating performance on written assessments to features of mathematics discussion. International Journal of Science and Mathematics Education, 18, 1375-1398. https://doi.org/10.1007/s10763-019-10029-w [ Links ]
Chan, M. (2020). A multilevel SEM study of classroom talk on cooperative learning and academic achievement: Does cooperative scaffolding matter? International Journal of Educational Research, 101, 101564. https://doi.org/10.1016/j.ijer.2020.101564 [ Links ]
Chiphambo, S.M., & Feza, N.N. (2020). Polygon pieces: Tools to address students' alternative conceptions and misunderstandings when learning of geometry. International Journal, 76(7), 191-208. https://doi.org/10.21506/j.ponte.2020.7.15 [ Links ]
Choy, B.H. (2014). Noticing critical incidents in a mathematics classroom. Mathematics Education Research Group of Australasia.
Cobb, S.C.J. (2012). 'You use your imagination': An investigation into how students use 'imaging' during numeracy activities. Master's thesis, University of Canterbury. Retrieved from http://ir.canterbury.ac.nz/handle/10092/7168 [ Links ]
Corovic, E. (2022). Summary: It's more than just share time. Australian Primary Mathematics Classroom, 27(1), 3-7. [ Links ]
Dahl, H., Klemp, T., & Nilssen, V. (2018). Collaborative talk in mathematics-Contrasting examples from third graders. Education 3-13, 46(5), 599-611. https://doi.org/10.1080/03004279.2017.1336563 [ Links ]
Duval, R. (2006). A cognitive analysis of problems of comprehension in a learning of mathematics. Educational Studies in Mathematics, 61(1-2), 103-131. https://doi.org/10.1007/s10649-006-0400-z [ Links ]
Gibbons, S.J. (2012). Manipulatives and the growth of mathematical understanding. Masters' dissertation, Brigham Young University. [ Links ]
Gülkilik, H., Moyer-Packenham, P.S., Ugurlu, H.H., & Yuruk, N. (2020). Characterizing the growth of one student's mathematical understanding in a multi-representational learning environment. The Journal of Mathematical Behavior, 58, 100756. https://doi.org/10.1016/j.jmathb.2020.100756 [ Links ]
Gülkilik, H., Ugurlu, H.H., & Yürük, N. (2015) Examining students' mathematical understanding of geometric transformations. Using the Pirie-Kieren Model. Educational Sciences: Theory and Practice, 15(6), 1531-1548. [ Links ]
Hardman, J., & Lilley, W. (2023). iLearn? Investigating dialogical interaction with tablets in mathematics lessons. Technology, Pedagogy and Education, 32(3), 1-15. https://doi.org/10.1080/1475939X.2023.2193194 [ Links ]
Hähkiöniemi, M., Francisco, J., Lehtinen, A., Nieminen, P., & Pehkonen, S. (2023). The interplay between the guidance from the digital learning environment and the teacher in supporting folding back. Educational Studies in Mathematics, 112(3), 461-479. https://doi.org/10.1007/s10649-022-10193-x [ Links ]
Hunter, R., & Civil, M. (2021). Collaboration in mathematics: Taking a sociocultural perspective. Avances de Investigación en Educación Matemática, 19, 7-20. https://doi.org/10.35763/aiem.v0i19.413 [ Links ]
Kim, J.H. (2016). Narrative data analysis and interpretation: Flirting with data. In J. Kim (ed.), Understanding narrative inquiry: The crafting and analysis of stories as research (pp. 185-224). SAGE Publications.
Lamb, J.T., & Geiger, V. (2012). Teaching experiments and professional learning. Springer.
Liang, W., & Fung, D. (2021). Fostering critical thinking in English-as-a-second-language classrooms: Challenges and opportunities. Thinking Skills and Creativity, 39, 100769. https://doi.org/10.1016/j.tsc.2020.100769 [ Links ]
Mabotja, K.S. (2017). An exploration of folding back in improving Grade 10 students' reasoning in geometry. Master's dissertation, University of Limpopo. Retrieved from: http://hdl.handle.net/10386/1805 [ Links ]
Martin, L.C. (2008). Folding back and the dynamical growth of mathematical understanding: Elaborating the Pirie-Kieren theory. The Journal of Mathematical Behavior, 27(1), 64-85. https://doi.org/10.1016/j.jmathb.2008.04.001 [ Links ]
Martin, L.C., & Towers, J. (2015). Growing mathematical understanding through collective image making, collective image having, and collective property noticing. Educational Studies in Mathematics, 88(1), 3-18. https://doi.org/10.1007/s10649-014-9552-4 [ Links ]
Mercer, N. (1996). The quality of talk in children's collaborative activity in the classroom. Learning and Instruction, 6(4), 359-377. https://doi.org/10.1016/S0959-4752(96)00021-7 [ Links ]
Mercer, N. (2008). Three kinds of talk (p. 1). University of Cambridge, Thinking Together. Retrieved from https://thinkingtogether.educ.cam.ac.uk/resources/5_examples_of_talk_in_groups.pdf
Mercer, N., & Wegerif, R. (2004). Is 'exploratory talk' productive talk? In H. Daniels & A. Edwards (Eds.), The RoutledgeFalmer Reader in psychology of education (pp. 67-86). RoutledgeFalmer.
Mercer, N., & Littleton, K. (2007). Dialogue and the development of children's thinking: A sociocultural approach. Routledge.
Mercer, N., Wegerif, R., & Dawes, L. (1999). Children's talk and the development of reasoning in the classroom. British Educational Research Journal, 25(1), 95-111. https://doi.org/10.1080/0141192990250107 [ Links ]
Molina, M., Castro, E., & Castro, E. (2007). Teaching experiments within design research. The International Journal of Interdisciplinary Social Sciences, 2(4), 435-440. https://doi.org/10.18848/1833-1882/CGP/v02i04/52362 [ Links ]
Moore, K.C., Stevens, I.E., Paoletti, T., Hobson, N.L., & Liang, B. (2019). Pre-service teachers' figurative and operative graphing actions. The Journal of Mathematical Behavior, 56, 100692. https://doi.org/10.1016/j.jmathb.2019.01.008 [ Links ]
Pirie, S., & Kieren, T. (1994). Growth in mathematical understanding: How can we characterise it and how can we represent it? Educational Studies in Mathematics, 26(2-3), 165-190. https://doi.org/10.1007/BF01273662 [ Links ]
Pirie, S., & Martin, L. (2000). The role of collecting in the growth of mathematical understanding. Mathematics Education Research Journal, 12(2), 127-146. https://doi.org/10.1007/BF03217080 [ Links ]
Polkinghorne, D.E. (1995). Narrative configuration in qualitative analysis. In J.A. Hatch & R. Wisniewski (Eds.), Life history as narrative (pp. 5-23). The Falmer Press.
Radebe, N., & Mushayikwa, E. (2023). Bloom's taxonomy and classroom talk: Exploring the relationship between the nature of small group discussion tasks and the quality of learners' talk. African Journal of Research in Mathematics, Science and Technology Education, 27(1), 1-11. https://doi.org/10.1080/18117295.2023.2172037 [ Links ]
Røsseland, M., Drageset, O.G., Sjåstad, S., Cangemi, E., & Bertolini, M. (2022, February). Using roles and positions to foster explorative talk in mathematics. In Twelfth Congress of the European Society for Research in Mathematics Education (CERME12) (pp. 1-8), Bolzano (en ligne), Italy.
Sfard, A. (2008). Thinking as communicating: Human development, the growth of discourses, and mathematizing. Cambridge University Press.
Soysal, Y. (2019). Indicators of productive classroom talk and supporting discourse moves: A systematic review for effective science teaching. Academy Journal of Educational Sciences, 3(2), 114-137. https://doi.org/10.31805/acjes.642246 [ Links ]
Steffe, L.P., & Thompson, P.W. (2000). Teaching experiment methodology: Underlying principles and essential elements. In R. Lesh & A.E. Kelly (Eds.), Research design in mathematics and science education (pp. 267-307). Erlbaum.
Towers, J., & Martin, L. C. (2014). Building mathematical understanding through collective property noticing. Canadian Journal of Science, Mathematics and Technology Education, 14(1), 58-75. https://doi.org/10.1080/14926156.2014.874612 [ Links ]
T'Sas, J. (2018). From emo to ratio: Exploratory talk as a need for group efficacy. In Proceedings of the Third International Conference on Language Education and Testing, 26-28 November 2018, Antwerp, Belgium/Simons, Mathea [edit.]; Smits, Tom FH (pp. 184-191).
Webb, P., Whitlow, J.W., & Venter, D. (2017). From exploratory talk to abstract reasoning: A case for far transfer? Educational Psychology Review, 29(3), 565-581. https://doi.org/10.1007/s10648-016-9369-z [ Links ]
Wegerif, R., & Mercer, N. (1997). A dialogical framework for researching peer talk. Language and Education Library, 12, 49-64. [ Links ]
Wei, C.S., & Ismail, Z. (2010). Peer interactions in computer-supported collaborative learning using dynamic mathematics software. Procedia-Social and Behavioral Sciences, 8, 600-608. https://doi.org/10.1016/j.sbspro.2010.12.083 [ Links ]
Wright, V. (2014). Frequencies as proportions: Using a teaching model based on Pirie and Kieren's model of mathematical understanding. Mathematics Education Research Journal, 26(1), 101-128. https://doi.org/10.1007/s13394-014-0118-7 [ Links ]
Yao, X. (2020). Characterizing learners' growth of geometric understanding in dynamic geometry environments: A perspective of the Pirie-Kieren theory. Digital Experiences in Mathematics Education, 6, 293-319. https://doi.org/10.1007/s40751-020-00069-1 [ Links ]
Yao, X. (2021). Tracing learners' growth of mathematical understanding in a dynamic geometry environment: Networking multiple theories. Khon Kaen, Thailand 19-22 July 2021, p. 303.
Yao, X., & Manouchehri, A. (2022). Folding back in students' construction of mathematical generalizations within a dynamic geometry environment. Mathematics Education Research Journal, 34(2), 241-268. https://doi.org/10.1007/s13394-020-00343-w [ Links ]
 Correspondence:
Correspondence:
Kabelo Chuene
kabelo.chuene@ul.ac.za
Received: 14 Aug. 2022
Accepted: 18 July 2023
Published: 30 Nov. 2023














