Services on Demand
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
Pythagoras
On-line version ISSN 2223-7895
Print version ISSN 1012-2346
Pythagoras vol.44 n.1 Cape Town 2023
http://dx.doi.org/10.4102/pythagoras.v44i1.742
ORIGINAL RESEARCH
Solving quadratic equations by completing the square: Applying Newman's Error Analysis Model to analyse Grade 11 errors
Tšhegofatšo P. Makgakga
Department of Mathematics Education, College of Education, University of South Africa, Pretoria, South Africa
ABSTRACT
Error analysis is an instructional strategy that can assist teachers to identify learners' areas of weakness in mathematics and that can point to remediation of those errors. This article explores the errors learners exhibit when solving quadratic equations by completing the square using Newman's Error Analysis Model. A research study explored the errors learners exhibit when solving quadratic equations by completing the square. Newman's Error Analysis Model provided the analytic framework for the qualitative approach that was used to explore those errors. A diagnostic test with five test items was administered to 35 learners in one secondary school in Limpopo province of South Africa. Subsequently, 12 learners whose scripts featured common mistakes were identified; these learners participated in a semi-structured interview to diagnose the errors. The findings revealed that learners commit comprehension, transformation and process errors. The findings suggest that if the errors that learners make are exposed and made explicit, the errors can be remediated and thereby enhance understanding and learning. The findings of this study indicate that for teachers to understand the types of errors learners commit when solving quadratic equations by completing the square it is vital for them (errors) to be addressed. Mathematics teachers should also consider diagnosing why learners commit those errors, as they would know the strategies to be employed to teach this topic and subsequent topics.
CONTRIBUTION: The findings of this article add value to the current literature by providing empirical knowledge on learner challenges when solving quadratic equations by completing the square. This study provides opportunities for mathematics teachers to focus more on the strategies that would assist learners to understand this topic
Keywords: error analysis; quadratic equations; comprehension errors; transformation errors; process errors.
Introduction
A quadratic equation (QE) is an algebraic equation of the second degree with one variable (Harripersaud, 2021; Kabar, 2018). Tendere and Mutambara (2020) note that a QE is an equation written in standard form as ax2 + bx + c = 0 with a ≠ 0, where a, b and c are constants and x is an unknown variable. Kabar (2018) and Hu et al. (2022) posit that learners can solve QEs by using three identified methods: factorisation, completing the square (CS) and using the quadratic formula. In South Africa (SA), quadratic equations are introduced to learners in Grade 10, whereas learners start with quadratic expressions in Grade 9.
Quadratic equations are a branch of mathematics that cut across all spheres and that need to be taught and learned in secondary schools (Cahyani & Rahaju, 2019). Quadratic equations is a compulsory and important topic to be learned in secondary school mathematics as it bridges the gap between functions, polynomial derivatives, and linear equations (Kim How et al., 2022). Kim How et al. (2022) argue that besides connecting with linear equations, QE is a vital branch of mathematics that is applicable in solving problems in engineering and structural design, physics, as well as in real-life modelling and word problems. According to Yeow et al. (2019), QE seems to be an easy topic to learn which involves basic skills that can be applied in sports and architecture. At school level learners are required to solve QE problems in examinations and standardised tests and here it is found that they have serious challenges because they do not master the topic (Thomas & Mahmud, 2021). Although QE is seen as an easy, important and compulsory topic in mathematics, it seems to be more difficult to learn and master compared to other mathematical topics (Güner, 2017). The challenges learners face in mastering QE lead them to commit errors and these errors need to be known by both teachers and learners.
According to Sari and Jailani (2019), the difficulties experienced by learners when solving mathematical problems can be caused by learners' weaknesses of lack of knowledge and understanding of the concept. This conceptual misunderstanding causes learners to commit errors when solving QE (Hu et al., 2022). As such, Thomas and Mahmud (2021) note that it is important for teachers to identify the difficulties and errors in advance to address them as early as possible to prevent learners from committing the same or more errors in other related topics. It is also advantageous for learners to be notified of the errors they commit, in order to understand the root cause of those errors. If errors are made clear to learners, they can identify the misconceptions they possess for teachers to know the strategies that can be used to address those misconceptions. Correcting the misconceptions that learners possess may lead to conceptual understanding of QE. This will then eliminate the errors learners commit.
Finzer and Bennett (1995) describe errors as learners' incorrect answers in addressing the problem at hand and caused by following incorrect procedures to solve those problems in mathematics. Kaufmann et al. (2022) view errors as mistakes, slips or misunderstanding of learners when solving mathematical problems. Slips and errors are distinguished by Gardee and Brodie (2021). It is found that errors mainly occur at a deeper conceptual level than slips (Kaufmann et al., 2022). Gardee and Brodie (2015) add that errors are systematic and caused by misconceptions, due to overgeneralisation of prior knowledge. Learner errors in the mathematics classroom can be the most natural and inevitable of all the interactions (Rushton, 2018). They (errors) can either be seen as an opportunity to learn or be a problem that can be avoided in mathematics teaching (Ingram et al., 2015). Gardee and Brodie (2021) postulate that learners can learn better if their errors are discussed during the lessons rather than being corrected or avoided in the mathematics classroom. It is important for teachers not to avoid or ignore learner errors to enable them to understand why they committed those errors (Sari & Jailani, 2019). Gardee and Brodie (2015) add that teachers need to identify and evaluate learner errors, interpreting them from the perspective of those learners. Errors can occur in QE when learners use CS to determine the values of unknown variables. Alhassan and Agyei (2018) describe CS as a technique used to solve QE by changing the form to make the left-hand side take the perfect square form. To solve the QE ax2 + bx + c = 0 by CS, according to Laridon et al. (2010), learners need to make the coefficient of x2 be 1, when a ≠ 1; they need to divide by the coefficient or multiply by the multiplicative inverse of that constant number. The learners need therefore to divide both sides by that coefficient before they can find the additive inverse of 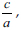 , for example
, for example 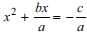 . In addition, the learners should then add the square of half the coefficient of x to both sides and square it before factorising the equation:
. In addition, the learners should then add the square of half the coefficient of x to both sides and square it before factorising the equation: 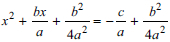 . Then the learners can factorise the equation on the left-hand side and simplify the right-hand side (Pretorius et al., 2006). The factors on the left-hand side are
. Then the learners can factorise the equation on the left-hand side and simplify the right-hand side (Pretorius et al., 2006). The factors on the left-hand side are 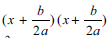 and the right-hand side would be
and the right-hand side would be 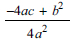 . Completing the square method is regarded as difficult and is taught to high-achieving learners who may sometimes abandon it to apply factorisation or the quadratic formula (Foster, 2022). Foster (2022) notes that learners prefer to use factorisation and quadratic formula than CS when solving QE. Mostly, learners use CS to solve QE that are difficult to factor (Alhassan & Agyei, 2018).
. Completing the square method is regarded as difficult and is taught to high-achieving learners who may sometimes abandon it to apply factorisation or the quadratic formula (Foster, 2022). Foster (2022) notes that learners prefer to use factorisation and quadratic formula than CS when solving QE. Mostly, learners use CS to solve QE that are difficult to factor (Alhassan & Agyei, 2018).
Problem statement
To the best of the researcher's knowledge, solving QE by CS with Grade 11 learners using Newman's Error Analysis Model (EAM) is rarely investigated (Newman, 1977). Learners in Grade 11 need to know this topic as it is introduced in Grade 10; however, it has been established that it is problematic for learners to solve QE by CS. Even pre-service teachers have found solving QEs by CS difficult (Alhassan & Agyei, 2020). The Institute of Education Chief examiners' report for algebra and geometry (2018) concurs that undergraduate students pursuing a Bachelor of Education failed to answer questions that expect them to use CS to solve QEs in the form ax2 + bx + c = 0. Learners appear to exhibit errors that are associated with content understanding and misconceptions. However, mathematics teachers in most schools, like the ones that participated in this study, do not treat the errors that learners make seriously; hence, such problems are exacerbated from one grade to the next. Informed discussions between the researcher and some concerned teachers revealed the same challenges that Grade 11 learners face in solving QE. Grade 11 learners' poor performance when solving mathematical problems brought to the fore the importance of conducting this research project. Subsequent discussions with the teachers led to a decision to administer a diagnostic test to help them identify the source of their errors. The diagnostic test found that what was challenging was for Grade 11 learners to master solving QEs using either CS, factorisation, or the quadratic formula. One challenge learners face is solving QE by CS. Makgakga (2016) investigated errors when solving QE by CS with Grade 11 learners; however, the author did not elaborate on how those errors occurred using Newman's EAM. Using Newman's EAM, this article intends to exhibit the errors and the reasons why Grade 11 learners make those errors when solving QE by CS. In addition, there is no study conducted in Limpopo province analysing errors in QE using this model. This article aims to explore the errors learners exhibit when solving QE by CS using Newman's EAM and in so doing make teachers and learners aware of those errors.
Research objectives and questions
This article sought to explore the errors learners exhibited in relation to Newman's EAM when solving QE by CS in Grade 11 mathematics. Using Newman's EAM as a lens, the focus was on the comprehension error type, transformation error type and processing error type. This lens enabled the researcher to understand how learners explain and solve QE by CS, as well as their attributions of the sources of those errors. Methods of inquiry included semi-structured interviews and the outcomes of a diagnostic test to identify and diagnose errors learners exhibit in solving QE by CS, to make teachers aware of the pattern of the errors learners display to know the strategies teachers can employ when teaching this topic. The objectives of the article are to:
-
Identify the errors learners exhibited when solving QE by CS using Newman's EAM.
-
Diagnose the reasons why learners exhibited those errors.
The research questions were, therefore: (1) What types of errors, classified in terms of Newman's EAM, do Grade 11 learners exhibit in solving QE by CS? (2) Why do learners exhibit those errors when solving QE by CS?
This article argues that Grade 11 learners have challenges in solving QE by CS and many exhibit errors that should have been addressed in Grade 10. The learners were found to have comprehension, transformation and processing errors when solving QE by CS. This study revealed learners' lack of prior conceptual knowledge that could have taken the form of introduction to QE in Grades 10 and 11.
This article begins with a brief discussion of the SA curriculum orientation towards QE, errors in QE and the difficulties learners experience in solving QE, as found in the scholarly literature. Newman's EAM is also discussed as a framework underpinning this study and explains the research methodology espoused to collect and analyse data that answer the research questions. Finally, strategies to be used by teachers, curriculum developers, mathematics specialists and textbook writers to address the errors and their cause in solving QE by CS are recommended.
South African curriculum orientation towards quadratic equations
Quadratic equations in the SA curriculum context is introduced in Grade 10 and both Grade 10 and Grade 11 learners should start solving the equations using factorisation (Curriculum and Assessment Policy Statement [CAPS], 2011). Quadratic equations differ from linear equations in that the latter has only one root, while QE can have two distinct solutions, one solution or no solution (Version 1 CAPS Grade 10 Mathematics). Two methods in solving QE in Grade 11 are completing the square and applying the quadratic formula. Solving QE by CS provides a way to derive a quadratic formula that can be used to solve QE.
Literature review
Studies have demonstrated that most learners struggle with QE (Kim How et al., 2022; Makgakga, 2016; Tendere & Mutambara, 2020). Tendere and Mutambara (2020) point out that most learners appear to experience difficulties in solving QE by both factoring and using quadratic formula methods. The difficulties in solving QE can be caused by teacher-centred strategies' emphasis on memorisation of procedures or steps. Kim How et al. (2022) identify challenges in solving QE as a lack of teaching strategies, teaching aids, learners' acceptance of concepts and procedures, and their thinking capabilities. One of the challenges learners faces in solving QE may be due to the high rate of misconceptions that lead to errors.
Makgakga (2016) found that Grade 11 learners committed conceptual and procedural errors when solving QE by CS. A study by Tendere and Mutambara (2020) adds that learners exhibit conceptual, procedural and technical errors when solving QE. The scholars argue that a conceptual error can be a misunderstanding of facts and concepts and result in failure to understand the relationship of concepts involved. Procedural errors can occur when learners follow incorrect procedures to solve mathematical problems. Learners need to have good background knowledge of mathematics to apply rules, methods and procedures to solve problems (Makgakga, 2016). Technical errors can be caused by the misapplication of learned procedures which can be the result of carelessness, a slip or silly mistakes (Tendere & Mutambara, 2020). Thomas and Mahmud (2021) add that errors in QE can be caused by a lack of understanding of basic concepts and learners' learning styles.
Some types of errors identified are cognitive, as revealed in Díaz et al.'s (2020) study with high school learners in Les Lagos in Chile. The study found that errors in solving QE problems could be due to predominating procedural difficulties. Agustyaningrum et al. (2018) note that these types of errors are manifested by both theoretical and conceptual content. To address these errors, teachers need to implement an intervention for learners to learn subsequent concepts (Díaz et al., 2020). In addition, Thomas and Mahmud (2021) used a diagnostic test with 30 Form 4 learners to diagnose errors they commit when solving QE. Their study revealed that learners showed comprehensive and transformation errors; few of them committed encoding errors and no reader error was found.
Errors in QE committed by learners were also investigated by Abubaker (2017). The study revealed that the majority of learners display multiplicative errors, additive errors, incorrect choices of coefficients and wrong treatment of fractions errors when solving QE. Other errors revealed were choosing the coefficient of the second degree of the variable while the coefficient of the first degree is a fraction. However, a general deficit was found in empirical evidence explaining errors using Newman's EAM when solving QE by CS, especially in SA.
Errors exhibited by learners when solving QE can recur and as a result affect learners' learning of subsequent concepts (Sari & Jailani, 2019). Learner errors need to be identified to avoid their recurrence in subsequent concepts and grades. In the context of this study, errors need to be identified and diagnosed and Grade 11 learners need to be aware of the errors to avoid committing them in the final-year examination and subsequently in higher education algebra and related concepts.
Theoretical lens
Newman's (1977) EAM was used to underpin this study. The EAM is a model teachers use to identify and categorise learner errors in mathematics. Newman notes that learners experience consecutive hurdles when solving mathematical problems which lead them to commit errors (Chusnul et al., 2017). Therefore, this model in this study is used to identify and diagnose the types of errors learners commit in solving QE. Newman has identified five types of errors learners display in solving mathematical problems; those are: reading, comprehensive, transformative, processing and encoding errors.
The EAM has gained popularity in mathematics education on error analysis and has proven to be reliable in classifying and categorising learners' errors. The approach is also used by Clarkson (1991), Santoso et al. (2017), Sumule et al. (2018), Singh et al. (2010), and Mahmud et al. (2020) in their research work. Clarkson shows that a higher frequency of learners exhibited comprehension errors while Sumule et al. reveal that most learners exhibit both transformation and comprehension errors. Mahmud et al. in their 2020 study reveal processing errors when solving mathematical problems which could lead to transformation errors. According to Kenys and Firda (2018), error analysis needs to be done to identify the stage at which errors occur when learners solve mathematical problems. Learners need to know how to overcome five successive diagnostic errors to solve mathematical problems (Newman, 1977).
As earlier noted, successive diagnostic errors identified by Newman when solving mathematical problems are reading, comprehensive, transformative, processing and encoding. These errors are outlined as follows:
-
The reading stage examines learners' ability or inability to read the statements to identify the key elements or main points relevant to the question to prepare for the next stage.
-
The second error type is the comprehensive stage that determines the learners' inability or ability to comprehend the mathematical statements, break the problem into smaller chunks and make sense of it.
-
The third error type is the transformation stage which determines the ability or inability to choose mathematical operations or methods, and correct or incorrect procedures to solve mathematical problems.
-
The fourth error type is the processing stage in which learners execute mathematical procedures correctly or incorrectly.
-
Lastly, the encoding error type is where the learner can write the correct or incorrect answer but cannot justify the answer or provide the conclusion of the given answer.
Error analysis is important for teachers and researchers as it helps them to choose the appropriate approaches, strategies, instructional media and models to alleviate learners' errors in mathematics (Fitriani et al., 2018). This study has used this model to determine learners' ability or inability to solve QE by CS. This study has adapted the model to include comprehension error, transformation error and processing error as the researcher needed to understand how learners, firstly, understand the role of each term in the equation and, secondly, change the original equation into the new equation in preparation for the third phase of processing that equation.
Research methods and design
Study design
This qualitative exploratory case study design explored the errors learners exhibited in solving QE by CS and the reasons why those learners exhibit those errors applying the EAM. An exploratory case study is a way to understand what is happening, ask questions, seek new insights and assess a phenomenon in a new light (Yin, 1994). Swaraj (2019) posits that exploratory case study provides an in-depth analysis of a topic, formulating problems that are more precise and gaining insights of a phenomenon. This study has used Newman's EAM to view the data collected within it to make sense of them.
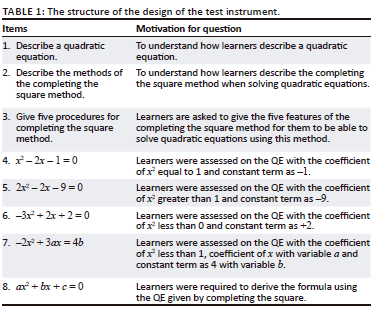
A diagnostic test was administered to 35 Grade 11 learners (19 female and 16 male) in one of the rural secondary schools in the Limpopo province of SA. Eight QE problems adapted from previous Grade 11 examination papers (Table 1) were distributed to all sampled learners and the test took 50 minutes to complete. To validate the test instrument, the researcher requested two mathematics education lecturers and two mathematics teachers who had taught mathematics for more than 10 years to moderate it.
All learners' scripts were gathered immediately after they were completed and marked on the same day. A day after marking the test scripts, the researcher conducted semi-structured interviews of 15 minutes with four male and six female learners, purposively selected according to the types of errors committed in their assessment scripts to understand why they committed those errors. At the time of data collection, learners had learned QE by factorisation, CS, and using the quadratic formula according to the departmental curriculum guidelines, termed a pace setter. The researcher used the EAM during the interviews to determine the errors learners made when solving QE by CS. The collected data were analysed and interpreted by classifying and identifying error types according to Newman's (1977) error analysis: comprehension error, transformation error, reading error, processing error and encoding error.
The researcher sought permission from a Grade 11 mathematics teacher and learners to participate in this study. The principal and head of department of mathematics and science in the school were informed about the research. The role and participation of learners was explained prior the inception of the study. Privacy and confidentiality of the learners was protected before and after the study. Consent forms were signed by the learners who were under 18 years of age at the time of the study to confirm their participation.
Methodological approach
This section describes how Newman's EAM is used to analyse the data sets collected for this study. The main concepts of the framework are defined and the performance indicator is described. The main concepts are comprehension error, reading error, transformation error, processing error, and encoding error.
Results
The analysis of the findings applying Newman's (1977) EAM includes a reading error, transformation error, processing error, comprehension error, and encoding error. Five question items were used to analyse the errors exhibited by the learners when solving QE by CS. The findings revealed no reading errors as questions in the test instrument used only mathematical symbols and no word problems. Table 3 depicts the total number of errors according to test items, analysed with the EAM. Learners who participated in this study were coded as L1F, L2F, L3M and this means that learner 1 is female (L1F), learner 2 is female (L2F) and learner 3 is male (L3M), and question items are coded as QI1, QI2, QI3 and so on. The analysis in Table 3 used absolute numbers and percentages of the EAM error types.
Table 3 depicts no reading errors in all question items as questions in the assessment were not word problems, but mathematical symbols. The findings revealed compression errors, transformation errors, processing errors and few of the learners displayed encoding errors. Comprehension errors were found in QI1, QI2 and QI3 and during the interview stage of this study. Transformation and processing errors were identified in the learners' test scripts in QI4-QI8. Not many learners committed encoding errors and the analysis of the findings are based on comprehension, transformation and processing errors.
How learners describe quadratic equations and the completing the square method
Few learners described a QE as an equation that can be solved by factorisation, completing the square or using the quadratic formula. Abubaker (2017) states that a QE is an equation of the second degree with one variable, while Tendere and Mutambara (2020) describe a QE as an equation written in standard form as ax2 + bx + c = 0 where a, b and c are constants and x is an unknown variable. The learners described QE using the methods, namely factoring, using the quadratic formula and CS to solve QE. This led to learners not knowing how to describe these identified methods. The samples in Figure 1 show how learners (L2F, L3M, & L5F) described QE in QI1.
Learners were not able to describe or define a quadratic equation in terms of concepts or mathematical ideas - they resorted to giving methods of solving the equation. This lack of conceptual understanding underlies some difficulties the learners experience in solving QE using either one of the methods. This QE topic cuts across all spheres and should be taught at secondary schools (Cahyani & Rahaju, 2019; Kim How et al., 2022; Tendere & Mutambara, 2020). Quadratic equations is an important topic that can be applied in solving problems in engineering and structural design, physics, as well as real-life modelling and word problems (Kim How et al., 2022).
However, most of the learners showed no comprehension in describing a QE for QI2 and QI3. Lack of comprehension is visible when a learner cannot describe what CS is when solving QE and know the five features of CS for them to solve QE using this method. Alhassan and Agyei (2018) describe CS as a technique used to solve QE by changing the form of the equation to make the left-hand side take a perfect square form. Clarkson (1991) shows that learners who are found to be in the comprehension stage need to demonstrate their ability to understand the concept. Most of the learners gave a limited explanation of solving QE by CS. They described CS as adding the square of half the coefficient of x when solving QE.
This evidence (Figure 2) supports the premise that learners describe CS as adding half the coefficient of x when solving QE. Learners lacking comprehension in describing CS can lead them to commit transformation and processing errors when solving QE. This support Foster (2022) that solving QE by CS can be difficult, and they may prefer to use factoring and quadratic formula as they are seen to be easy methods to use when solving QE. It is essential for learners to know how to describe what CS is in solving QE.
In addition to being unable to describe CS when solving QE, the majority of the learners could not mention the five features of CS (Laridon et al., 2010). They could only mention two features: finding the additive inverse of the constant term, 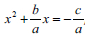 , and adding the square of half the coefficient of x on the left-hand and right-hand sides,
, and adding the square of half the coefficient of x on the left-hand and right-hand sides, 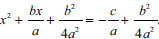 . The learners could not mention the three features: dividing by the coefficient of x2 if a ≠ 0, thus
. The learners could not mention the three features: dividing by the coefficient of x2 if a ≠ 0, thus 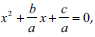 , factoring the left-hand side as the square of the trinomials,
, factoring the left-hand side as the square of the trinomials, 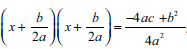 , and taking the square of both sides,
, and taking the square of both sides, 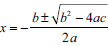 . In other words, learners lacked the understanding of steps to solve QE by CS which led them to commit errors when solving the equations. Makgakga (2016) suggests that these features can provide the background knowledge of solving QE by CS, for learners to apply the correct procedures, methods and rules to find the solutions. Furthermore, if learners do not understand facts and concepts, they fail to make sense of the concepts and tend to use incorrect procedures to solve QE problems (Tendere & Mutambara, 2020). This challenge is manifested by conceptual and theoretical content (Agustyaningrum et al., 2018). In addressing this issue, teachers need to be aware of this lack of theoretical and conceptual content when solving QE using CS to suggest possible ways of addressing those challenges.
. In other words, learners lacked the understanding of steps to solve QE by CS which led them to commit errors when solving the equations. Makgakga (2016) suggests that these features can provide the background knowledge of solving QE by CS, for learners to apply the correct procedures, methods and rules to find the solutions. Furthermore, if learners do not understand facts and concepts, they fail to make sense of the concepts and tend to use incorrect procedures to solve QE problems (Tendere & Mutambara, 2020). This challenge is manifested by conceptual and theoretical content (Agustyaningrum et al., 2018). In addressing this issue, teachers need to be aware of this lack of theoretical and conceptual content when solving QE using CS to suggest possible ways of addressing those challenges.
How learners transform quadratic equations using the completing the square method
Transformation errors were also revealed in the learners' scripts as they appeared not to know the mathematical operations, correct procedures, or methods in solving mathematical problems (Newman, 1977). This error type shows that learners could not interpret the terms of QE in order to solve them by CS. Table 2 depicts a high percentage of the transformation error type in QI4 and QI5 with 48.6% and 57.1%. Examples of transformation errors are shown in Figure 3.

Learners revealed transformation errors as they could not correctly interpret the three terms in the equation; they followed the incorrect procedures to change the equation. Predominant procedural challenges can lead learners to commit errors when solving mathematical problems (Díaz et al., 2020). The learners showed that they had shallow understanding of the question items where they should complete the square by adding the square of half the coefficient of x in the equation. This is one of the features that learners need to pay attention to when they solve QE by CS which leads them to commit transformation errors. This showed that this concept is difficult to learn and master (Güner, 2017) compared to factoring and using the quadratic formula when solving QE. However, learners could not realise that the coefficient of x2 should be equal to 1 before they could add the square of half the coefficient of x. This can be caused by misapplication of learned procedures (Tendere & Mutambara, 2020), when changing the equation to use CS to solve QE. Two learners had challenges in the transformation stage as they chose incorrect procedures to approach the question item, in which the coefficient of x needs to be realised as 1 after multiplying the whole equation by the multiplicative inverse of 2, the coefficient of x2, which is 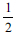 . This concurs with Abubaker's (2017) study where the majority of learners displayed multiplicative errors when solving QE.
. This concurs with Abubaker's (2017) study where the majority of learners displayed multiplicative errors when solving QE.
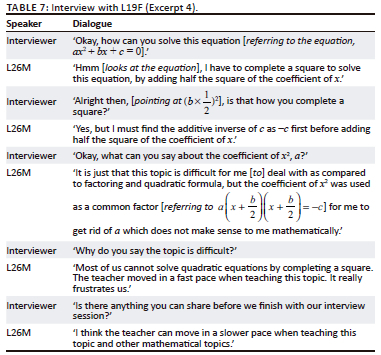
In the interview sessions learners who were selected to explain how they answered the QE questions showed difficulties when solving QE by CS. They seem to have misunderstood the topic as they could not justify the procedures used to solve QE problems and three of them (1 male and 2 female) indicated that the strategies used to teach this topic were not easy to understand. Table 4 is the interview conducted with L8M and L9F whose scripts were used in Figure 3 and who displayed transformation error type. The interviews intended to understand how learners answered the questions.

The two excerpts (Table 4 and Table 5) depict that learners do not know the features of CS to transform the original equation into a new equation and this led to transformation errors. Lacking the knowledge of transformation in solving QE using CS can be affected by the learners knowing these two features: finding the additive inverse of the constant term and adding half the coefficient of x. This concurs with Foster's (2020) study that the majority of learners find using CS to solve QE difficult and prefer to use factoring and the quadratic formula. Some learners like L9F could not apply the addition of the square of half the coefficient of x when solving QE by CS, as they apply this step on the left-hand side only instead of applying both on the left- and right-hand sides. Learners need to have good background knowledge to apply methods, rules and procedures to mathematical problems (Makgakga 2016).
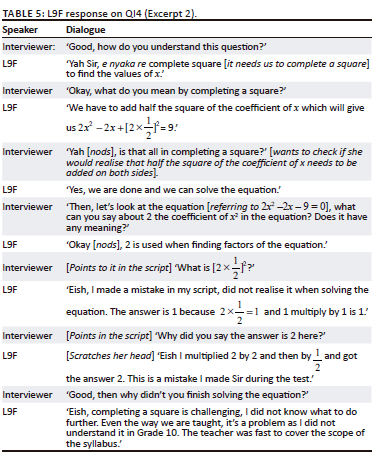
Another reason why learners display transformation errors is that of multiplying both sides by the multiplicative inverse of 2, which is the coefficient of x2, a ≠ 1. Multiplying by the multiplicative inverse of x2 where a ≠ 1 and finding the additive inverse of the constant term are the first two essential features that can assist learners to change the original equation to a new equation to complete a square. Here, the new equation was supposed to be 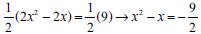 after applying the first and second features of CS when solving QE. This supports what Abubaker (2017) found, that the majority of learners commit additive errors, multiplicative errors and incorrect choices of the coefficients of the equations. Lack of attention to underlying mathematical concepts, namely an equation, is another reason found that learners commit transformation errors when solving QE by CS.
after applying the first and second features of CS when solving QE. This supports what Abubaker (2017) found, that the majority of learners commit additive errors, multiplicative errors and incorrect choices of the coefficients of the equations. Lack of attention to underlying mathematical concepts, namely an equation, is another reason found that learners commit transformation errors when solving QE by CS.
The learner showed little understanding of what has to be done to solve QI2 by CS. The transformation error type is identified as L9F did not know that the coefficient of x2 needs to be equal to 1 before adding the square of half the coefficient of x to change the equation to 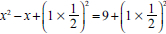 . L9F's transformation error was that the learner could not correctly transform the equation into
. L9F's transformation error was that the learner could not correctly transform the equation into 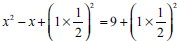 as she used incorrect procedures or mathematical operations or methods to transform it. The interview shows that teaching approaches used to teach QE by CS is a challenge as teachers are rushed to finish the scope of the syllabus.
as she used incorrect procedures or mathematical operations or methods to transform it. The interview shows that teaching approaches used to teach QE by CS is a challenge as teachers are rushed to finish the scope of the syllabus.
How learners execute quadratic equations using the completing the square method
The other error type found in this study is, according to the EAM framework, a processing error. The processing error type is when learners follow incorrect procedures or mathematical operations or methods to execute the problem (Newman, 1977). Although all question items recorded processing errors when solving QE problems, a higher percentage of errors was found in QI4 and QI5 where learners could not correctly solve QE problems. Learners at this stage multiplied by 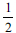 only on the left-hand side instead of multiplying both sides by
only on the left-hand side instead of multiplying both sides by 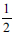 . In the case of QE with the coefficient of x2 greater than or less than 1, errors occurred when learners could not make the coefficient of x2 equal to 1 which led them to use incorrect procedures to solve the equations.
. In the case of QE with the coefficient of x2 greater than or less than 1, errors occurred when learners could not make the coefficient of x2 equal to 1 which led them to use incorrect procedures to solve the equations.
L19F and L26M in their scripts (Figure 4) revealed a lack of comprehension of the equations which led them to commit transformation errors; hence, they could not correctly complete the square on both sides and then solve the problem. L19F used an incorrect coefficient of x as 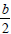 instead of
instead of 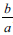 , while L26M completed the square without making the coefficient of x2 equal 1. Although L19F and L26M followed the wrong procedures to solve the equation, there is consistency in procedures used in the process to arrive at the answer.
, while L26M completed the square without making the coefficient of x2 equal 1. Although L19F and L26M followed the wrong procedures to solve the equation, there is consistency in procedures used in the process to arrive at the answer.

Tables 6 and 7 looked for the reasons why learners answered QI8 using their respective procedures. The two tables with excerpts revealed learners experiencing difficulties in solving QI8 using the equation ax2 + bx + c = 0 to derive the formula 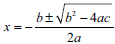 by CS. The only reason why they grappled with the execution of this equation by CS is that they did not know the first feature, multiplying by the multiplicative inverse of the coefficient of x2, which is a where a ≠ 1, and the second feature of adding the square of half the coefficient of x, which led them to commit processing errors. The cause of processing error here could be that learners could not solve this QI8 by changing the form of the equation to make the left-hand side take a perfect square form (Alhassan & Agyei, 2018) and lacked the relevant knowledge, learning styles or experience related to the concept (Thomas & Mahmud, 2021). The learners also gave the reason that the topic is difficult to deal with as compared to factoring and using the quadratic formula. These findings concur with the Foster (2022) study that solving QE by CS is found to be difficult for learners, even to high-achieving learners who also prefer to use factoring and the quadratic formula to solve QE. These tables with excerpts also reveal that the teacher's approaches contribute to the errors committed by learners when solving QE by CS. This is also found by Kim How et al. (2022) that learners' errors when solving QE can be used in teachers' strategies, which need to be given attention to address errors that learners commit. Learners need to have a good background knowledge of mathematical concepts to apply methods, rules and procedures to solve problems (Makgakga, 2016).
by CS. The only reason why they grappled with the execution of this equation by CS is that they did not know the first feature, multiplying by the multiplicative inverse of the coefficient of x2, which is a where a ≠ 1, and the second feature of adding the square of half the coefficient of x, which led them to commit processing errors. The cause of processing error here could be that learners could not solve this QI8 by changing the form of the equation to make the left-hand side take a perfect square form (Alhassan & Agyei, 2018) and lacked the relevant knowledge, learning styles or experience related to the concept (Thomas & Mahmud, 2021). The learners also gave the reason that the topic is difficult to deal with as compared to factoring and using the quadratic formula. These findings concur with the Foster (2022) study that solving QE by CS is found to be difficult for learners, even to high-achieving learners who also prefer to use factoring and the quadratic formula to solve QE. These tables with excerpts also reveal that the teacher's approaches contribute to the errors committed by learners when solving QE by CS. This is also found by Kim How et al. (2022) that learners' errors when solving QE can be used in teachers' strategies, which need to be given attention to address errors that learners commit. Learners need to have a good background knowledge of mathematical concepts to apply methods, rules and procedures to solve problems (Makgakga, 2016).

Discussion
This study intended to explore the errors learners exhibit when solving QE by CS. This study revealed a higher rate of comprehension, transformation, and processing skills. No reading error was identified, and a low rate of encoding error was found. Tendere and Mutambara (2020) and Kim How et al. (2022) concur that learners experience challenges in solving QE. In comprehension errors, learners grappled with the description of QE and CS. In addition, most of the learners could not mention and interpret the five essential features of CS when solving QE, especially with equations with a coefficient of x2 not equal to 1 (a ≠ 1). For example, multiplication mistakes were revealed as most learners could not multiply by the multiplicative inverse of the coefficients of x2 in QI5-QI8 to prepare for the transformation stage. This comprehension error type could be the result of the misapplication of the learned procedures caused by carelessness, slips or silly mistakes committed by learners (Tendere & Mutambara, 2020). Makgakga (2016) notes that learners need to have a good background to apply rules, methods and procedures to solve problems. The underlying concepts have to be taught first, for example additive inverse, multiplicative inverse, linear equation, factorisation of QE expressions and solving QE by squaring both sides.
In the transformation error type, learners grappled with QE problems when completing the square on both sides, as most of them completed the square on one side; as such, the coefficient of x2 was not made 1. Similar findings are found by Mahmud et al. (2020) where learners committed transformation and processing errors and few learners had encoding errors. Most of the learners struggled to transform the equations, for example from 2x2 - 2x - 9 = 0 to 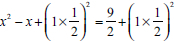 , to prepare for the processing stage. Abubaker (2017) concurs that the majority of learners displayed multiplicative errors, wrong treatment of fractional errors, additive errors, and incorrect choices of coefficients when solving QE. Abubaker further notes learners' errors exhibited when choosing the coefficient of the second degree of the variable, when the coefficient of the first degree is a fraction.
, to prepare for the processing stage. Abubaker (2017) concurs that the majority of learners displayed multiplicative errors, wrong treatment of fractional errors, additive errors, and incorrect choices of coefficients when solving QE. Abubaker further notes learners' errors exhibited when choosing the coefficient of the second degree of the variable, when the coefficient of the first degree is a fraction.
The other error type was found at the processing stage where learners were expected to use procedures to determine the values of x of the QE. Processing errors can occur because of the misapplication of methods, rules, and procedures to solve problems, and predetermined procedural difficulties (Díaz et al., 2020). Most of the learners experienced difficulties when multiplying terms in the brackets, for example 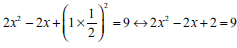 , which showed that the learner had multiplied 2 × 2 = 4 and then multiplied 4 by
, which showed that the learner had multiplied 2 × 2 = 4 and then multiplied 4 by 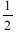 to get the answer 2. Makgakga (2016) reveals Grade 11 learners' conceptual errors and procedural errors when solving QE by CS. This showed that these errors can recur in Grade 11; however, learners at this stage are not expected to exhibit these types of errors when solving QE by using one of the QE methods: factorisation, CS and using the quadratic formula. Sari and Jailani (2019) concur that these types of errors learners make when solving QE can recur and affect the learning of subsequent concepts.
to get the answer 2. Makgakga (2016) reveals Grade 11 learners' conceptual errors and procedural errors when solving QE by CS. This showed that these errors can recur in Grade 11; however, learners at this stage are not expected to exhibit these types of errors when solving QE by using one of the QE methods: factorisation, CS and using the quadratic formula. Sari and Jailani (2019) concur that these types of errors learners make when solving QE can recur and affect the learning of subsequent concepts.
No reading error was identified, and this is supported by Thomas and Mahmud's (2021) study where no reading error was identified when learners solve QE problems. This is because the QE question items were not word problems which did not require a lot of reading. Few learners displayed encoded errors and as such learners could not get the solutions to the equations.
Conclusion
This study explored the errors learners exhibit when solving QE by CS using Newman's EAM. It argues that Grade 11 mathematics learners need to have a good background in QE by factorisation, CS and using the quadratic formula to avoid making errors when solving QE problems. The study revealed that learners committed comprehension errors, transformation errors and processing errors when solving QE by CS.
Firstly, the comprehension error type showed learners grappling to describe QE and CS. The study revealed learners misinterpreting and not mentioning the five key features of CS, especially with equations where the coefficient of x is not equal to 1 (a ≠ 1). Most of the learners could not multiply by the square of half the coefficient of x. This challenge could be attributed to the procedural steps learned during the teaching of solving QE by CS, which contributed to learners who viewed QE with a coefficient of x2 equal to 1 (a ≠ 1) and other ones not equal to 1 (a ≠ 1) in the same way.
Secondly, the transformation error type included multiplicative errors, additive errors and incorrect choices of coefficients when preparing to solve the equations. Most learners treated the equations the same when applying CS, adding the square of half the coefficient of x on one side of the equation. Lastly, in processing error type, learners showed misapplied methods and used wrong rules and procedures to solve QE by CE. This study indicated that the previous error type can affect another error type. Comprehension errors can lead learners to commit transformation errors and processing errors. Therefore, learners need to possess comprehensive knowledge of QE and other concepts to address transformation and processing errors. If learner errors are not identified and addressed in advance, they will recur and impede the learning of subsequent concepts. Teachers should be empowered to determine strategies to teach this concept to prevent learner errors in solving QE by CS.
Learners' errors need the teachers' intervention for learners to learn subsequent concepts (Díaz et al., 2020). Further studies can be done with Grade 11 learners investigating errors in QE using the two methods: factorisation and the quadratic formula.
Acknowledgements
The author acknowledge the participants of this study who wrote a diagnostic test and took part in the semi-structured interviews. The author also acknowledge Prof. Caroline Long who critically reviewed the manuscript and Ms Joyce Musi who contributed to language editing.
Competing interests
The author declare that he has no financial or personal relationships that may have inappropriately influenced him in writing this article.
Author's contributions
T.P.M. is the sole author of this article.
Ethical considerations
An ethical clearance certificate was obtained from the College of Education Ethics Committee, reference number: 2022/02/09/90197607/14/AM.
Funding information
This research received no specific grant from any funding agency in the public, commercial, or not-for-profit sectors.
Data availability
The authors confirm that the data supporting the findings of this study are available within the article.
Disclaimer
The views and opinions expressed in this article are those of the author and do not necessarily reflect the official policy or position of any affiliated agency of the author.
References
Abubaker, I. (2017). Error analysis in solving simultaneous and quadratic equations in some selected senior secondary schools in Sabon Gari Zaria in Kaduna State. Journal of Science, Technology & Education, 5(1), 198-209. [ Links ]
Agustyaningrum, N., Abadi, A., & Mahmudi, A. (2018). An analysis of students' errors in solving abstract algebra tasks. Journal of Physics: Conference Series. 1097. 012118. https://doi.org/10.1088/1742-6596/1097/1/012118 [ Links ]
Alhassan, M.N., & Agyei, D.D. (2018). Colleges of Education mathematics tutors problems and challenges associated with the teaching of quadratics using completing a square approach. International Journal of Science and Research, 9(2), 1842-1853. Retrieved from https://www.ijsr.net/archive/v9i2/SR20212181653.pdf [ Links ]
Alhassan, M.N., & Agyei, D.D. (2020). Examining colleges of education mathematics tutors' conceptions in teaching completing the square in Ghana. International Journal of Scientific and Research Publications, 10(3), 253-261. https://doi.org/10.29322/ijsrp.10.03.2020.p9927 [ Links ]
Cahyani, L., & Rahaju, E.B. (2019). Students' reflective abstraction of middle school in reconstructing quadratic equation concepts based on high mathematical ability. Journal of Physics: Conference Series, 1417(1), 012044. https://doi.org/10.1088/1742-6596/1417/1/012044 [ Links ]
Chusnul, C., Mardiyana, & Retno, D.S. (2017). Errors analysis of problem solving using the Newman stage after applying cooperative learning of TTW type. In AIP conference proceedings, 1913, Malang, 2-3 August. https://doi.org/10.1063/1.5016662
Clarkson, P.C. (1991). Language comprehension errors: A further investigation. Mathematics Education Research Journal, 3(2), 25-33. https://doi.org/10.1007/BF03217225 [ Links ]
Curriculum and Assessment Policy Statement (CAPS). (2011). CAPS for further education and training phase. Department of Education.
Díaz, V., Aravena, M., & Flores, G. (2020). Solving problem types contextualized to the quadratic function and error analysis: A case study. EURASIA Journal of Mathematics, Science and Technology Education, 16(11), 1-16. Retrieved from https://files.eric.ed.gov/fulltext/EJ1285007.pdf [ Links ]
Finzer, W., & Bennett, D. (1995). Technology tips: From drawing to construction with The Geometer's Sketchpad. Mathematics Teacher, 88(5), 428-431. https://doi.org/10.5951/MT.88.5.0428 [ Links ]
Fitriani, H.N., Turmudi, T., & Prabawanto, S. (2018). Analysis of students' error in mathematical problem solving based on Newman's Error Analysis. In International conference on mathematics and science education of Universitas Pendidikan Indonesia (Vol. 3, pp. 791-796). Retrieved from https://www.semanticscholar.org/paper/Analysis-of-students-error-in-mathematical-problem-Fitriani-Turmudi/60fe875b2fd606db83043b33e846a778ce2381a8
Foster, C. (2022). Starting with completing the square. Mathematics in Schools. Retrieved from www.m-a.org.uk
Gardee, A., & Brodie, K. (2015). A teacher's engagement with learner errors in her Grade 9 mathematics classroom. Pythagoras, 36(2), 293. https://doi.org/10.4102/pythagoras.v36i2.293 [ Links ]
Gardee, A., & Brodie, K. (2021). Relationships between teachers' interactions with learner errors and learners' mathematical identities. International Journal of Science and Mathematics Education, 20(1), 193-214. https://doi.org/10.1007/s10763-020-10142-1 [ Links ]
Güner, P. (2017). High school students' achievement of solving equations. Bartin University Journal of Faculty of Education, 6(2), 447-467. https://doi.org/10.14686/buefad.277494 [ Links ]
Harripersaud, A. (2021). The quadratic equations concept. American Journal of Mathematics and Statistics, 11(3), 67-71. [ Links ]
Hu, Q., Son, J.W., & Hodge, L. (2022). Algebra teachers' interpretation and responses to student errors in solving quadratic equations. International Journal of Science and Mathematics Education, 20, 637-657. https://doi.org/10.1007/s10763-021-10166-1 [ Links ]
Ingram, J., Pitt, A., & Baldry, F. (2015). Handling errors as they arise in whole-class interactions. Research in Mathematics Education, 17(3), 183-197. https://doi.org/10.1080/14794802.2015.1098562 [ Links ]
Institute of Education-UCC. (2018). Chief examiners report for Algebra and Geometry. Institute of Education.
Kabar, M.G.D. (2018). Secondary school students' conception of quadratic equations with one unknown. International Journal for Mathematics Teaching and Learning, 1, 112-129. https://doi.org/10.4256/ijmtl.v19i1.94 [ Links ]
Kaufmann, O.T., Larsson, M., & Ryve, A. (2022). Teachers' error‑handling practices within and across lesson phases in the mathematics classroom. International Journal of Science and Mathematics Education, 21, 1-26. https://doi.org/10.1007/s10763-022-10294-2 [ Links ]
Kenys, F.Z., & Firda, F.A. (2018). Error analysis of Newman to solve Geometry problem in terms of Cognitive Style. Advances in Social Science, Education and Humanities Research, 160, 24-27. https://doi.org/10.2991/incomed-17.2018.5 [ Links ]
Kim How, R.P.T., Zulnaidi, H., & Abdul Rahim, S.S. (2022). HOTS in quadratic equations: Teaching style preferences and challenges faced by Malaysian teachers. European Journal of Science and Mathematics Education, 10(1), 15-13. https://doi.org/10.30935/scimath/11382 [ Links ]
Laridon, P., Barnes, H., Kitto, A., Myburg, M., Rhodes-Houghton, R., Sasman, M., Scheiber, J., & Sigabi, M. (2010). Classroom mathematics. Grade 11 Learner's book. Heinemann Publishers (Pty) Ltd.
Mahmud, M.S., Zainal, M.S., Rosli, R., & Maat, S.M. (2020). Dyscalculia: What we must know about students' learning disability in mathematics? Universal Journal of Educational Research, 8(12B), 8214-8222. https://doi.org/10.13189/UJER.2020.082625 [ Links ]
Makgakga, S. (2016). Errors and misconceptions in solving quadratic equations by completing a square. Association for Mathematics Education of South Africa. Retrieved from https://acesse.dev/9dp5D
Newman, M.A. (1977). An analysis of 6th grade pupils' errors on written mathematical tasks. In M.A. Dlm. Clements & J. Foyster (Eds.), Research in mathematical education in Australia (pp. 239-258). Hutchinson, Inc.
Pretorius, J., Pretorius, J., Potgieter, R., & Ladewig, W. (2006). Oxford mathematics plus. Grade 11 learner's book. Oxford University Press Southern Africa.
Rushton, S.J. (2018). Teaching and learning mathematics through error analysis. Fields Mathematics Education Journal, 3(1), 1-12 https://doi.org/10.1186/s40928-018-0009-y [ Links ]
Santoso, D.A., Farid, A., & Ulum, B. (2017). Error analysis of students working about word problem of linear program with NEA procedure, Journal of Physics: Conference Series, 855(1). https://doi.org/10.1088/1742-6596/855/1/012043 [ Links ]
Sari, I.F.D.P., & Jailani, J. (2019). Error analysis for grade IX students in completing the materials of quadratic equations. Annals of Mathematics Models, 1(2), 64-80. [ Links ]
Singh, P., Rahman, A.A., & Hoon, T.S. (2010). The newman procedure for analyzing primary four pupils errors on written mathematical tasks: A Malaysian perspective. University Technology MARA.
Sumule, U., Amin, S.M., & Fuad, Y. (2018). Analysis of junior high school students' errors in solving HOTS geometry problems based on Newman's error analysis. Journal of Physics: Conference Series, 11(12), 947012053. https://doi.org/10.1088/1742-6596/1321/3/032131 [ Links ]
Swaraj, A. (2019). Exploratory research: Purpose and process. Parisheelan, XV(2), 666-670. [ Links ]
Tendere, J., & Mutambara, L.H.N. (2020). An analysis of errors and misconceptions in the study of quadratic equations. European Journal of Mathematics and Science Education, 1(2), 81-90. https://doi.org/10.12973/ejmse.1.2.81 [ Links ]
Thomas, D.S., & Mahmud, M.S. (2021). Analysis of students' error in solving quadratic equations using Newman's procedure. International Journal of Academic Research in Business and Social Sciences, 11(12), 222-237. https://doi.org/10.6007/IJARBSS/V11-I12/11760 [ Links ]
Yeow, P.C., Thavamani, R., Kamalah, R., Wong, J.W., & Santhanasamy, V.D. (2019). Buku Teks Matematik Tingkatan Empat. Penerbit Pustaka Yakin.
Yin, R. (1994). Case study research: Design and methods (2nd ed.). Sage.
 Correspondence:
Correspondence:
Tšhegofatšo Makgakga
makgatp@unisa.ac.za
Received: 14 Feb. 2023
Accepted: 22 Aug. 2023
Published: 07 Dec. 2023














