Services on Demand
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
Pythagoras
On-line version ISSN 2223-7895
Print version ISSN 1012-2346
Pythagoras vol.44 n.1 Cape Town 2023
http://dx.doi.org/10.4102/pythagoras.v44i1.728
ORIGINAL RESEARCH
Ascertaining Grade 10 learners' levels of mathematical modelling competency through solving simultaneous equations word problems
Rajendran Govender; Dzivaidzo Machingura
Faculty of Education, School of Science and Mathematics Education, University of the Western Cape, Cape Town, South Africa
ABSTRACT
Possessing mathematical competence is a pre requisite for independently comprehending, understanding and applying all features of mathematical modelling in a particular setting. This research study thus explores the mathematical modelling competencies that Grade 10 learners exhibit while solving contextual problems in a mathematics learning and teaching context, with specific reference to using mathematical modelling. Since mathematical modelling is a fairly new teaching strategy used in mathematics teaching some teachers may be ignorant of the skills and competencies required for learners to solve problems efficiently. A mixed-methods approach to this study was decided upon and a case study design used within an interpretative paradigm in an effort to ascertain the levels of mathematical modelling competencies of a non-random sample of 20 Grade 10 learners. Participant learners who attended a Western Cape school were requested to solve a set of word problems involving the use of simultaneous equations. Task based activities and observations were used as a means to collect data, as well as semi-structured interviews to gauge participating learners' views and experiences. Qualitative content analysis methods were employed together with basic descriptive statistical methods.
CONTRIBUTION: Research findings reveal the limited competence and abilities of the participating Grade 10 learners to make sense of, understand or constructively progress in solving contextual problems, and the challenges they experience to progress through particular stages of the modelling process, such as building and solving models and interpreting the solutions thereof
Keywords: mathematical modelling; problem-solving; quadratic equations; Grade 10 learners; word problems.
Introduction
The rationale for having pursued this research centres on what the title implies, namely to ascertain Grade 10 learners' levels of mathematical modelling competency through solving simultaneous equations word problems, by analysing strategies used, particular skills displayed, and the errors made during calculations in their efforts to solve the given problems. According to Durandt et al. (2021, p. 3), mathematical modelling competency is frequently described as a person's competency not only to construct but also to utilise mathematical models to solve real-world problems, and in addition analyse and compare models confronted. The mathematics modelling competencies (MMC) to be employed during mathematical modelling to be successful as stated by Tong et al. (2019, p. 20) include the ability to: clearly identify the problem, make valid assumptions and identify relevant variables, perform the required mathematics, analyse and assess the solution, iteration, and implementation of the model.
In terms of specific mathematics competencies, learners require mathematical skills to manipulate, analyse, synthesise, compare, generalise and work with abstract ideas (Bahmaei, 2011). Similarly, Tong et al. (2019), with reference to Dundar et al. (2012) emphasise particular essential skills required when dealing with mathematics content topics, such as:
[U]nderstanding, formalizing [sic] and applying the problems in diverse subject areas, employing the models by defining the simple relationships in the nature, and realizing [sic] the potentials and constraints of the models, commenting and discussing on the realities of the existing models and moving between the theoretical and practical aspects of modelling and problem-solving related to mathematics. (p. 20)
In this article the focus is on simultaneous equations in context, that is, the questions used in this research are presented as word problems, which may include solving two linear equations or a system of equations, consisting of one linear and one quadratic equation in two unknowns (Johari & Shahrill, 2020). Simultaneous equations word problems as mathematics content is considered an important aspect of algebra (Johari & Shahrill, 2020) in the Grade 10 mathematics curriculum, according to the Curriculum and Assessment Policy Statement (CAPS) (Department of Basic Education [DBE], 2011), which constitutes the current South African school curriculum. Solving these systems of simultaneous equations is essentially viewed as problem-solving (Nordin et al., 2017; Ugboduma, 2006, 2012; Yunus et al., 2016) which also involves certain procedures (for instance addition, subtraction, multiplication, division, substitution, etc.).
This research is pitched at the Grade 10 level specifically, since this grade forms the first year of a three-year Further Education and Training (FET) mathematics phase (Grade 10 to Grade 12). Consequently, it is essential that Grade 10 learners acquire a sound knowledge, and basic understanding of mathematical content essential to successfully complete the final summative Grade 12 (also referred to as Matric) final assessment. From anecdotal evidence and research literature (Johari & Shahrill, 2020; Nordin et al., 2017; Ugboduma, 2006, 2012; Yunus et al., 2016), many learners clearly encounter difficulties solving simultaneous equation systems, that is, they always make some or other error. These said errors may be the result of misconceptions, which Johari and Shahrill (2020, p. 263) refer to as 'mathematical error[s] and irrational error[s]', procedural inaccuracies such as 'wrong substitution of the subject' (Johari and Shahrill, 2020, p. 263), or unforced errors through negligence, involving the basic operations such as multiplication, subtraction or division, involving mathematical tools such as additive inverse and multiplicative inverse. Yunus et al. (2016, p. 1551) refer to this as 'incompetency in learners' pre-requisite knowledge of addition and subtraction of integers'.
Problem statement
The systemic evaluation conducted by the South African National Department of Basic Education (2013) showed that learning and teaching of mathematics experience major challenges of underachievement on both primary and secondary school levels. The 2022 systemic test results reveal a substantial decrease in the pass rate of Grade 9 Mathematics as a serious concern (Western Cape Government, 2023). This would have definite implications for learners who still progress to Grade 10 despite obtaining low scores, with limited mathematics skills and content knowledge. Underachievement is especially evident in mathematics content requiring higher-order thinking and problem-solving, which point to substantial limitations in terms of learners' abilities to solve problems, especially those of the non-routine and real-world variety (Doorman et al., 2007).
Based on anecdotal evidence, many learners frequently experience difficulty making sense of what exactly is expected of them. Sepeng and Madzorera (2014) maintain the most challenging aspect of solving mathematical contextual problems to be understanding, and making decisions as to what method to follow. In this particular context, Seifi et al. (2012) advocate that it is important for mathematics teachers to present algebraic contextual problems to learners to facilitate successful solving of such problems.
The concept of 'algebraic contextual problems' was meant to indicate contextual problems, namely word problems that could be solved algebraically. Algebraically is an adverb, derived from the concept of algebra (a noun), an important branch of mathematics. Algebraic relates to and involves laws of algebra. Algebraic thinking includes recognising and analysing patterns, studying and representing relationships, making generalisations, and analysing how things change (Usiskin, 1999). At school level there are basically three ways of solving a system of two simultaneous equations algebraically, namely graphing, and substitution and elimination. Simultaneous equations, whether linear or quadratic, have the same unknown variables x and y and are solved simultaneously to determine the value of the variables. Variables are symbols, usually letters of the English alphabet, written to replace an unknown or changing or varying quantity (Epp, 2011; Usiskin, 1999). Learners continue performing poorly in tasks or items requiring thinking on a higher level and problem-solving (Johari and Shahrill, 2020). Hence, this study seeks to track and analyse mathematical modelling competencies Grade 10 learners demonstrate as they solve word problems with the ultimate goal to enhance learning and teaching of mathematics. The resultant research question that emanates is as follows: What levels of mathematical modelling competency do Grade 10 learners demonstrate when solving word problems invoking simultaneous equations?
Towards a description of mathematical modelling
Mathematical modelling is generally described as a problem-solving strategy whereby realistic contextual situations are represented as mathematical problems through mathematisation. Blum and Ferri (2009) are in agreement when they say that:
[M]athematical modelling (the process of translating between the real world and mathematics in both directions) is one of the topics in mathematics education that has been discussed and propagated most intensely during the last few decades. (p. 45)
The implication is that these word problems in essence are practical problems based on typical or common social settings and occurrences, approached and solved mathematically. The said nature of such problems could oblige learners to adopt mathematically accepted strategies, and align solutions to the social contexts.
The debate around the dual nature of mathematical modelling needs to be considered. Julie and Mudaly (2007) pose the question whether mathematical modelling should be employed to develop mathematics or whether it should simply be considered as content. They assert that:
[A] common notion associated with mathematical modelling as a vehicle is that mathematics should be represented in some context. The purpose for embedding mathematics in context is not the construction of mathematical models per se but rather the use of contexts and mathematical models as a mechanism for the learning of mathematical concepts, procedures, conjecturing and, at times, developing context-driven justifications for obtained conjectures. (p. 504)
This notion of doing mathematics in context aligns to that which realistic mathematics education advocates as briefly discussed below. In addition, they maintain that when mathematical modelling is employed as content it involves 'the construction of mathematical models of natural and social phenomena without the prescription that certain mathematical concepts, procedures or the like should be the outcome of the model-building process' (Julie and Mudaly, 2007, p. 504).
In terms of the concept 'realistic', Freudenthal (1968) maintains that mathematics should be intimately connected to reality, and remain closely linked to learners. He emphasises that the relevance of mathematics to society should be obvious in an effort to be of human value and engaged with as a human activity rather than mere subject matter. This perspective was also conveyed by Freudenthal in his 1968 lecture entitled 'Why […] teach mathematics so as to be useful'. As Goffree (1993) remarked, one of the essential passages of this lecture refers to mathematisation as a major characteristic of realistic mathematical education: 'What humans have to learn is not mathematics as a closed system, but rather as an activity, the process of mathematising reality and if possible even that of mathematising mathematics' (Freudenthal, 1968, p. 7). Consider this problem, taken from Blum (2011), to further explain the meaning of 'realistic':
In a sports centre on the Philippines, Florentino Anonuevo Jr. polishes a pair of shoes. They are, according to the Guinness Book of Records, the world's biggest, with a width of 2.37 m and a length of 5.29 m. Approximately how tall would a giant be for these shoes to fit? Explain your solution. (p. 16)
This problem is said to depict a real-life situation (Doorman et al., 2014). Learners likewise wear shoes as a matter of routine. In essence this closely relates to real-life experience, as the shoe's length and width dimensions are given in metres. Thus, the learner may feel compelled to solve the problem mathematically and interpret the answer to the real-life situation.
Changing the focus back to mathematical modelling, Blum and Ferri (2009, p. 47) maintain that the main aim of applying mathematical modelling in the mathematic class is to guide learners to construct a meaningful world in terms of understanding and supporting the learning of mathematics. This should be directly linked to mathematics concept development, comprehension, knowledge retention, and forming a positive predisposition to mathematics. Eric et al. (2012) similarly advocate mathematical modelling as crucial for concept development. Meanwhile Blum and Ferri (2009, p. 45) argue that 'in classroom practice all over the world, however, [mathemtical] modelling still has a far less prominent role than desirable', implying that gaps exist in solving mathematical word problems using mathematical modelling.
The compelling need for mathematical modelling
It is claimed that mathematical modelling as a teaching and learning strategy is considered vital for allowing learners of mathematics to engage in more intricate mathematics that involves contextual problems. As a result of this belief, Ärlebäck (2010) designed units based on the guidelines put forward in Activity Theory to introduce modelling to education institutions. Araújo (2010) stresses the fact that mathematical modelling has been integrated into school curricula internationally, and considered it to be an essential inclusion. In addition, contextual problems that result in systems of simultaneous equations ultimately compel learners to resort to using mathematical modelling as the preferred strategy. Learners with abilities to skilfully manoeuvre through modelling stages during problem-solving are prone to increase achievement in mathematics.
Blomhoj and Jensen (2003) offered six sub-processes to be followed when engaging in problems necessitating the use of mathematical modelling, namely:
-
Constructing a task or assignment, which is expected to assist the learner in identifying the properties or factors exibited in terms of the perceived reality that is to be modelled. These may refer to choosing the applicable objects and relations, from the ensuing domain of inquiry, and idealisation of these to ensure a meaningful mathematical representation.
-
Translating said objects and relations from their original mode of appearance in mathematics is crucial.
-
Applying mathematically sound mathematical approaches to realise precise outcomes and conclusions.
-
Interpreting outcomes.
-
Drawing conclusions.
-
Appraising the validity of the model by comparing perceived or anticipated data or with theoretically based knowledge (Blomhoj & Jensen, 2003, p. 125).
Having worked through and having mastered the processes mentioned, learners should be equipped to successfully attempt and basically solve most contextual problems (Jorgensen, 2014). Evidently there is a definite need for learners, as global citizens, to be instructed in the use of mathematical modelling to be productive citizens, equipped to face the future with confidence.
Basic competencies required for mathematical modelling
The term competence or competencies is the description commonly applied in research pertaining to education when referring to skills displayed through cognitive activity such as knowledge processing. Blomhoj (2003, p. 126) explained competence in terms of mathematical modelling as the skill to 'autonomously and insightfully carry through all aspects of [the] mathematical modelling process in a certain context'. Mathematical modelling is referred to as the 'creation and use of a mathematical model consisting of six sub-processes' by Blomhoj and Jansen, (2006). These were described as: (1) the formulation of tasks that will guide you to identify the characteristics of the perceived reality that should be modelled, (2) selection of the relevant objects based on the resulting domain in order to make a good mathematical representation, (3) the translation of objects and relations from their original mode to mathematics, (4) making use of mathematical methods to achieve mathematical results and conclusions, (5) interpreting results regarding the initiation of the domain, and (6) the 'evaluation of the validity of the model by comparing it to the predicted data'.
Mathematics education researchers generally concur that the improvement of mathematical modelling competence comprises all six sub-processes. Blomhoj (2003, p. 129) argues that 'working with full-scale mathematical modelling is [a] time consuming way of learning'. Maaß (2006) details the term 'modelling competency', and advocates that quite a few definitions for competencies, originating from terms from several of the science branches, exist, as well as dissimilarities in these competency types. Niss (2003) on the other hand labels mathematical competence as the ability to comprehend, evaluate, engage in, and use mathematics, in varying contexts, whether intra- or extra-mathematically.
These mathematical competencies extend much further than merely mental or cognitive abilities and skills. As Tanner and Jones (cited in Maaß, 2006, p. 116) maintain, the said competencies also relate to images of life and putting these into action. Effective modelling strategies necessitate that learners continually monitor the process; however, frequently this is non-existent (Blum & Ferri, 2009).
Blum and Kaiser (1997), Maaß (2006, p. 116) speak of dividing the greater modelling process into sub-competencies. They maintain that learners who are able and skilled to successfully establish a model based on reality have: (1) to make assumptions and simplify the situation, while recognising relevant quantities that affect the context, (2) to label and recognise significant variables, constructing relations between the variables, and (3) to search for available information and to differentiate between related and unrelated information. The implication is that when learners successfully construct working mathematical models derived from real models, they actually demonstrate abilities to: (1) mathematise quantities and their relations, (2) simplify quantities and their relations, if the need arises and minimise their numerical intricacy, and (3) allocate pertinent mathematical symbols, thus representing situations graphically.
They also maintain that when learners reveal skills that allow them to adequately solve mathematical problems it implies that they are ultimately able to: (1) apply heuristic strategies like decomposing the problem into its constituent parts and recognising relations to comparable problems, (2) restructure the problem or alter how the problem is perceived and (3) vary quantities as deemed necessary (Blum & Kaiser, 1997).
As far as the development of particular abilities is concerned, Maaß (2006) was convinced that the development of metacognitive competencies was essential. Metacognition is sometimes referred to as thinking about one's own thinking. Schoenfeld (1992) similarly described it as knowledge of the individual's own thinking to self-regulate during the course of problem-solving. Maaß emphasises the fact that metacognition largely deals with managing one's own thinking. Evidently, metacognition is central for advancing or growing related critical proficiencies such as independently dealing with challenging problems or in terms of self-regulated learning.
From the discussion of basic competencies required for mathematical modelling, it is evident from the title that the aim of this study is to ascertain learners' mathematical modelling competencies and related proficiencies through the use of particular mathematics content, namely by means of solving simultaneous equations. It thus becomes necessary to elaborate on what the solving of simultaneous equations entails in this context.
Learners' experiences in solving simultaneous linear equations
Constructing or establishing a system of simultaneous equations involves the question of how to build at least two independent equations, whether linear or quadratic, or of a higher degree, to solve for two variables. Consider, x + y = 1, and 3 = y + 2x. As previously indicated, to experience this as a meaningful exercise compels learners to operate on a certain level of cognitive development, which implies comprehending what information is contained in the problem. This also requires the ability to represent such information by means of particular symbols or by formulating suitable mathematical models. Suitable mathematical models refer to models that may be appropriate for learners in different grades. In the mathematical modelling context, Bassanezi (1994, p. 31) maintains that 'a mathematical model is almost always a system of equations or algebraic inequalities, differentials, integrals, etc, obtained through establishing relations among variables considered essential to the phenomenon under analysis'. Muthuri (2009, p. 231) similarly describes a mathematical model as a 'set of equations that represent interconnections in a system … written in terms of mathematical objects that correspond directly to physical quantities, called variables'.
Finding solutions to problems involving simultaneous equations with two unknown variables can of course be solved linearly, geometrically or graphically. The act of solving simultaneous equations provides learners with problem-solving skills that are worthwhile, and may leave them with a broad and deep understanding of the concept of variable, and of substituting numerical values for specific variables in formulae, expressions and equations. This implies translating contextual problems with variables into number sentences. It needs to be said that the CAPS (DBE, 2012) pertinently addresses the development of specific skills for effectively dealing with solving simultaneous equations.
Frequently learners experience difficulties constructing equations that appropriately and accurately display relationships between numerical values (Kieran, 2007), and learners need to be particularly cautious throughout the process of solving contextual questions. Drijvers et al. (2011) claim that numerous mistakes occur when crossing from arithmetic to algebra during solving of algebraic equations. Often mistakes made may be ascribed to certain conceptual constraints. Limited understanding or knowledge gaps, and errors, whether procedural, factual or conceptual, tend to occur quite frequently, which may also be indicative of particular misconceptions that exist within learners. Furthermore, these miscalculations could be the result of incorrectly applying certain mathematical laws, rules or theorems.
Theoretical framework
The design and execution of this research study are underpinned by the modelling competency framework assimilated by Blum and Kaiser (1997, p. 9). In terms of this study, mathematical modelling competency is viewed as the ability to criss-cross each of the respective phases, as articulated in Figure 1 which constitutes the modelling process, when solving a given problem (Govender, 2018).
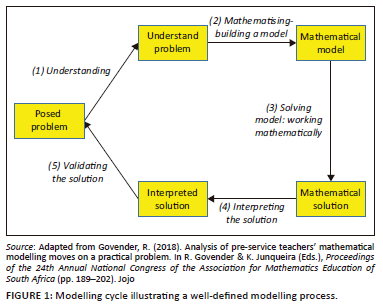
The mathematical modelling process, as depicted in Figure 1, is cyclic by nature and consists of five stages. The stages need to be transitioned in an effort to reach a mathematically acceptable solution to a practical problem. The stages, in order, are: (1) reading and understanding a problem, (2) mathematising the situation to build a mathematical model, (3) working mathematically within the context of the mathematical model to generate a mathematical solution, (4) interpreting the solution, and (5) validating the interpreted solution.
The problem-solving through modelling process begins with, and requires, complete understanding of the problem itself. As such the learner needs to be able to figure out exactly what the problem is about and what is required to solve it meaningfully (Pólya, 1973). By arranging and structuring the problem, the learner would facilitate sense-making and understanding. Arranging and structuring involve making assumptions, and recognising and labelling relevant and irrelevant quantities. Built into this process are the identification and construction of meaningful relationships linked to essential variables. Learners are also required to identify and construct relationships between key variables (Blum & Kaiser, 1997). Grasping of mathematical problems thus depends to a great extent on certain abilities related to visualisation and drawing in an effort to simplify the context or situation and overcome possible hurdles in the process of constructing the most suitable mathematical model (Schaap et al., 2011).
Developing appropriate structures and visuals of problems is essential for picking and identifying the proper quantities or values contained in the problem to allow for mathematisation (Brady, 2018). Translating a real problem into mathematical structures and formulas is referred to as mathematising (Brady, 2018; Niss, 2015). The expectation thus is that learners would develop in a way that equips them to differentiate between mathematical knowledge that is deemed acceptable and functional, and that which is irrelevant and unsuitable to assist learners in amicably solving the problem at hand. Implicit in this are the methods and procedures used, the heuristic approaches applied and the types of instruments used to be applied mathematically toward generating a mathematical solution. It is thus crucial that whatever the mathematical solution may be, it is aligned with the set constraints and parameters that govern the contextual problem. From here the solution needs to be translated to the mathematics language of practice so as to ensure a solution for the original contextual problem.
The modelling process culminates in some validation action, through which learners are required to demonstrate and substantiate their solutions in real terms. In addition, learners are expected to verify their explanations and answers to identify erroneous reasoning when compared to the original assumptions, or identify mathematical slip-ups in their mathematical calculations. Furthermore, learners need to get into the routine of ascertaining whether solutions fit the context. According to Oberholzer (1992), the validation phase may be used as a means of simulating the original practical problem through a group of varied assumptions and parameters influencing such assumptions. Blum and Kaiser (1997), cited in Maaß (2006, p. 117), maintain that the act of validation in fact affords space and opportunity to find alternate methods of finding solutions to the same problem.
Mathematical modelling is not one-directional, but sequential and cyclic. Niss (2015, p. 1445) claims that 'an actual solution model may go through steps in a different order and the strips may be intrinsically entangled'. Likewise, learners are unlikely to progress though cycle stages sequentially according to Ferri (2006, p. 87) but rather 'sometimes jump directly from the real situation to the mathematical model or go forth and back several times between the real world and mathematics'.
According to Blum and Kaiser (1997, p. 9), also cited in Maaß (2006, pp. 116-117), in essence, five broad mathematical skills take effect, namely: (1) the ability to grasp the real problem in context and devise a suitable model aligned to reality, (2) the ability to devise a mathematical model taken from reality, (3) the ability to find solutions for particular mathematical questions within this mathematical model, (4) the ability to accurately understand and translate mathematical results in a real situation, and (5) the ability to corroborate the findings.
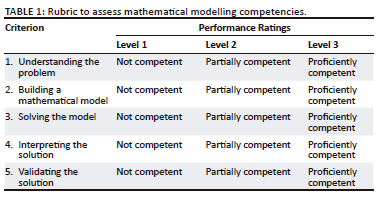
This theoretical framework formed the basis for the deductive qualitative analysis used in this study. The deductive qualitative analysis thus was conducted by constructing an analytical framework using the literature on mathematical modelling and the theoretical framework on mathematical modelling competencies as articulated by Blum and Kaiser (1997), as cited in Maaß (2006). To facilitate the construction of the analytical framework in the form of a rubric, an analytical rubric template specific to this study was used, as shown in Table 1.
Research methods and design
The descriptive case study design employed affords the opportunity to accurately describe the occurrences that transpired during the course of the study, including a description of the qualitative data collected (McMillan & Schumacher, 2012). The study focused on the Grade 10 learners from a technical high school in the Cape Metropole, Western Cape province, South Africa, situated 5 km from the University of the Western Cape. The school offers dual-medium education in English and Afrikaans, together with academic and technical subjects ranging from Grade 8 to Grade 12. The school offers academic subjects for Grade 8 to Grade 9 but academic and technical subjects for Grade 10 to Grade 12. Each grade has six classes with an average of 40 learners per class from Grade 8 to Grade 12. The school has a total of 1200 learners.
An uncontrolled quota sampling method (Bhardwaj, 2019) was used, which is a non-probability type of sampling to select subjects. The researchers made use of convenience selection consisting of three (3) classes of Grade 10 learners, taking technical mathematics. The participating classes (10A1, 10A2 and 10A3) comprised of 23 learners each. Learners in 10A1 were receiving technical mathematics in Afrikaans only, while those in 10A2 and 10A3 used English as the medium of teaching. One of the researchers was teaching 10A3 - for this reason it was convenient to have these learners as participants. This researcher thus used learners belonging to her and her colleagues, namely classes 10A1 and 10A2 as well.
From a group of 69 learners, a sample of 20 learners (13 girls and 8 boys) volunteered to participate in this study. They were of mixed Xhosa home language speaking and Afrikaans home language speaking learners. Their ages ranged from 15 to 17 years.
Written timeous feedback to task-based activities, explanations and descriptions were some of the tools used to elicit rich data from the research participants. A worksheet, observation and semi-structured interviews were used to collect the relevant data needed to provide answers to the research question. The worksheet contained a set of word problems associated with simultaneous equations, which learners had to solve in a double mathematics period of 80 minutes. The purpose of the worksheet was to determine learners' modelling competencies, by ascertaining how they solved problems pivoted around simultaneous equations using modelling steps, and to identify challenges and difficulties learners experienced during solving such problems. These five problems were selected from school textbooks with the aim to allow learners to read and understand the problem, select a strategy to solve the problem (including building a mathematical model), solve the problem (solve in their mathematical mode), and then interpret their solutions to see if they make sense. As learners were working through each problem individually, learners' strategies and moves in attempting to solve word problems were observed using a structured observation schedule. Observation was decided upon to complement the information provided by the participants to ensure credible information was gathered with regard to their levels of mathematical modelling competencies in solving word problems.
Semi-structured interviews were considered to be effective as a third strategy to collect rich qualitative data. The interviews with the learners were done after school hours for about 45 minutes for 5 days over the course of a week. Interviews were held after school so as not to interrupt the teaching and learning process during the normal school programme. The interview with each learner lasted about 10 minutes. An interview schedule was designed to ensure focus without imposing too much pressure on participants.
Analysis of the data
The simultaneous equations used in the study were considered as ideal since some significant algebraic processes are required to find solutions (Johari & Shahrill, 2020, p. 263). These specific problem-solving questions are considered challenging, require critical analysis and observation skills, and provide opportunities for discussion and interaction, according to Krulik and Rudnick (1993). Such problems also demand understanding particular mathematics concepts and application of skills. These specific problems test learners' ability to generate variables relevant to the problem situation, distinguish the relative importance of variables to build a meaningful model, identify specific questions crucial to the realistic problem, identify relationships between variables inherent to the problem situation, and select applicable relationships to the problem linked to the problem context (Burkem, 2018, cited by Govender, 2018).
The data were generated from the five contextual problems that Grade 10 learners had to work through to ascertain their modelling competencies. Due to limitations and constraints with respect to length of this article, only the analyses for questions 1 and 4 are discussed in detail. Certain observations with respect to questions 2, 3 and 5 are also shared. The five questions range from relatively simple to more advanced. The five questions posed were the following:
-
Problem 1: Half the sum of two numbers is 27 and their difference is 6. What are the numbers?
-
Problem 2: If 1 is added to the numerator and 2 to the denominator of a fraction, the ratio of the numerator to the new denominator is 2:3. If 1 is subtracted from the numerator and 2 from the denominator, the new numerator is equal to the new denominator. Find the fraction.
-
Problem 3: Andre has more money than Bob. If Andre gave Bob R20, they would have the same amount. While if Bob gave Andre R22, Andre would then have twice as much as Bob. How much does each one actually have?
-
Problem 4: In a two-digit number, the unit digit is thrice the tens digit. If 36 is added to the number, the digits interchange their place. Find the number.
-
Problem 5: If twice the age of son is added to age of father, the sum is 56. But if twice the age of the father is added to the age of son, the sum is 82. Find the ages of father and son.
Analysis of modelling competencies: Problem 1 in the worksheet
An expected solution for Problem 1 is as follows:
Let the larger number be x and the smaller number be y.
Half their sum = 27: therefore ½ (x +y) = 27……. (1)
Their difference = 6: therefore x - y = 6 ……. (2)
Multiply equation (1) by (2): Therefore, the answer will be x + y = 54 ……. (3)
Now add equation (2) and equation (3) to get rid of 1 variable (namely, y)
x - y = 6; x + y = 54
2x + 0 = 60 …… (4), so x = 30
Now substitute x = 30 in equation (3),
30 + y = 54 thus ∴ y = 30. So the numbers are 30 and 24.
Check: Difference: 30-24 = 6,
Half the sum of 2 numbers is 27: 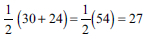
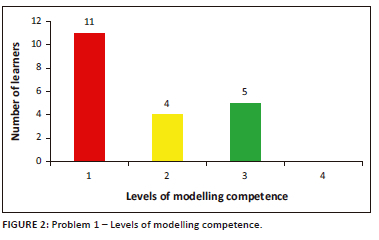
Figure 2 is a representation of the analysis of learners' responses to Problem 1. It indicates that 11 learners were assessed to be operating at level 1 modelling competence, four learners at level 2 modelling competence, and five learners at level 3 modelling competence.
Exemplification of level 1 modelling competence
Of 11 participating learners who operated on level 1 modelling competence, five made a deliberate effort to find a solution to the problem. Unfortunately, engaging in numerous mathematically erroneous operations and calculations, either through ignorance or negligence, led to incorrect answers. These five learners also seemed not to have been knowledgeable of what the question demanded of them. The other six learners on the other hand just jotted down the accurate solutions 24 and 30 without indicating calculations, or sharing related explanations. No assumptions governing the problem, associated with the sum and difference of two numbers, were mentioned by the learners. The usage of appropriate variable was absent, and incorrect relationships between 27 and 6 were given. The response by learner X is shared in Figure 3.

Learner X specifically showed no realisation that 27 was indeed the answer, namely the sum of half of the two given numbers that were posited in the problem. She wrongfully proceeded to find half of 27. During the interview, learner X was probed as to why she calculated half of 27; she responded as follows: 'I did not read the question well'.
Furthermore, learner X seemed to have had experienced a mental block as she could not figure out the quantities between which a difference of 6 existed, and consequently wrote down a totally wrong number sentence, namely '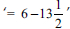 '. Upon probing learner X during the interview as to why she 'found half of 27' and wrote down '
'. Upon probing learner X during the interview as to why she 'found half of 27' and wrote down '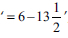 ', she responded as follows: 'I did not read the question well'.
', she responded as follows: 'I did not read the question well'.
These challenges that learners experienced in terms of reading with comprehension and inability to really understand the problem caused them not to progress toward a solution. As such, the predicament of not reading and comprehending the problem led learner Y to merely write down two numbers, as shown in Figure 4.

When learner Y was probed as to how she arrived at her solution, she replied by saying: 'Half of 20 is 10 and 27 take away 20 is 7, so I added 7 to 10 to get 17, and half of 10 is 5 plus 6 is 11 in the equation'.
Similarly to learner X, learner Y also jumbled up the relationships in terms of the given numerical values. Upon reflection it was clear that both of these participants failed to give an indication of having used representations through mathematisation. All of the learners - X, U, V, Y and P - failed to make any effort to come up with a suitable mathematical model, neither could they build a system of simultaneous linear equations.
Participant learners U, V, X, Y and P hardly revealed any grasp of the mathematical concepts concerned; in fact their replies and reasoning were mathematically flawed. It was also noticed that participants U, V, X, Y and P did not reflect on the correctness or validity of their solutions.
Grade 10 learners, in the initial stage of FET, should be able to formulate equations by means of variables and solve these simultaneously. The pertinent steps followed in the calculation should be clearly indicated. Unfortunately, 6 of the 11 participants merely jotted down what they considered to be the answer, namely 24 and 30. Figure 5 depicts a similar scenario in a brief single line reply from learner G.
To the question 'How did you get to the answers 24 and 30?', learner G responded: 'I multiplied 27 by 2 and got 54 and then subtracted 24 from 54 to get 30, I also subtracted 3 from 27 and I got 24'. She could not give a reason why she subtracted 3 from 27, saying: 'I do not know'.
The participant (learner G) multiplied 27 by 2 to get 54 which meant she succeeded in devising a strategy to find the sum of the two unknown numbers. Finding the sum of 54 is essential to get the ultimate solution to the problem. Even though learner G was unable to provide reasons for subtracting 3 from 27 to obtain 24, she should have noticed that 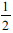 of 6 was 3 (which was the difference between the two unknown numbers), which she subtracted from 27 (which was half the sum of the two unknown numbers) to arrive at 24. It is unclear why this learner initially subtracted 24 from 54 to get to 30. Ultimately the strategies and procedures applied to produce 24 and 30 were devoid of appropriate mathematical justification and accuracy.
of 6 was 3 (which was the difference between the two unknown numbers), which she subtracted from 27 (which was half the sum of the two unknown numbers) to arrive at 24. It is unclear why this learner initially subtracted 24 from 54 to get to 30. Ultimately the strategies and procedures applied to produce 24 and 30 were devoid of appropriate mathematical justification and accuracy.
From the outset it was apparent that the learners struggled to make proper sense of the content and appeared to be overwhelmed. They clearly experienced major difficulties to comprehend what they were reading in the word problem. The stress was evident on their facial expressions and their anxiety levels were clearly higher than usual.
Exemplification of level 2 modelling competence
Four learners, who revealed level 2 competences, made efforts to construct systems of linear equations, which were either incomplete or flawed. Figure 6 indicates learner C's response as an example. There is no doubt that learner C grasped certain aspects pertaining to the given problem. The ability to assign variables x and y to the two numerical values stated in the problem serve as proof. The initial algebraic illustration of the statement 'half the sum of two numbers is 27' was accurately represented as 'half sum = 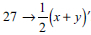 '. Efforts to translate the latter equation to a comparable relationship failed, since it was erroneously articulated as "∴ sum = 54 → 2(x + y). This could possibly be ascribed to the incorrect doubling of 27 to obtain 54. Instead, however, of doubling
'. Efforts to translate the latter equation to a comparable relationship failed, since it was erroneously articulated as "∴ sum = 54 → 2(x + y). This could possibly be ascribed to the incorrect doubling of 27 to obtain 54. Instead, however, of doubling 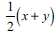 to obtain (x + y) the learner doubled (x + y) to find 2 (x + y). The elucidation of the statement 'and their difference is 6' was conceptually accurate as stated by the linear algebraic equation, x - y = 6 These steps prove that learner C successfully identified all the essential numerical values related to the problem and linked them to variables, x and y, and advanced to build relationships between them.
to obtain (x + y) the learner doubled (x + y) to find 2 (x + y). The elucidation of the statement 'and their difference is 6' was conceptually accurate as stated by the linear algebraic equation, x - y = 6 These steps prove that learner C successfully identified all the essential numerical values related to the problem and linked them to variables, x and y, and advanced to build relationships between them.

Except for the blunder, ∴ sum = 54 → 2 (x + y), all of the other relationships were suitably constructed and assimilated to form the system of simultaneous linear equations indicated below:
2x + 2y = 54 ……(1)
x − y = 6 ……(2)
The system of simultaneous linear equations assimilated by learner C is indicative of his cognitive ability, showing that he was able to create a usable model to solve the given problem, although the model itself was somewhat faulty. The learner evidently made a computational mistake simplifying 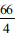 to obtain
to obtain 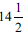 and not
and not 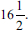 . Subsequently he ended up with
. Subsequently he ended up with 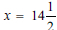 and not
and not 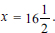 . This raised questions about the learner's number fluency and consequent ability to apply mathematical procedures appropriately and manipulate numerical values such as fractions. The learner persisted with the error throughout without any additional computational errors to arrive an answer of
. This raised questions about the learner's number fluency and consequent ability to apply mathematical procedures appropriately and manipulate numerical values such as fractions. The learner persisted with the error throughout without any additional computational errors to arrive an answer of 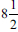 . Notwithstanding what can be considered a minor mistake, the learner evidently grasped the salient steps in the procedures in the computation. Also, learner C made no effort to interpret or to validate the solution within the given context.
. Notwithstanding what can be considered a minor mistake, the learner evidently grasped the salient steps in the procedures in the computation. Also, learner C made no effort to interpret or to validate the solution within the given context.
Exemplification of level 3 modelling competence
Only five learners exemplified level 3 modelling skills as indicated in Figure 7. The assumptions shared by these participating learners are indicative of their high level of understanding and the degree to which they managed to comprehend what was expected of them. These particular assumptions are formulated in terms of the unknown numerical values linked to the problem, the matching variables allocated to the number, and building of meaningful relationships between the variables. Their ways of mathematising were more advanced regarding formulating mathematical relationships and building of mathematical models represented by systems of two linear equations. These five learners successfully solved their respective mathematical models. One of the detailed responses (of learner Z) from this group is shared in Figure 7.
The initial statement, 'let the larger number be x and the smaller number be y', is sound, showing that the participant displays an awareness of the difference that occurs between the numbers. The said values are different and therefore one value must be larger than the other to result in a difference of 6. This compelled the learner to assign variables to the values identified, namely the larger number to be x and the smaller number to be y. Through the process of mathematisation the assumptions were transformed into strategic linear relationships as expressed in the system of linear equations below:
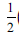 (x + y) = 27 …(1)
(x + y) = 27 …(1)
(x − y) = 6 ……(2)
By constructing linear equations such as 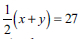 and x - y = 6 the learner demonstrated the required conceptual understanding of the statements 'half their sum is equal to 27' and 'their difference is 6'. The learner thus possesses the required cognitive capacity and skills to construct and use representations such as algebraic equations and construct a mathematical model to assist in solving the given problem.
and x - y = 6 the learner demonstrated the required conceptual understanding of the statements 'half their sum is equal to 27' and 'their difference is 6'. The learner thus possesses the required cognitive capacity and skills to construct and use representations such as algebraic equations and construct a mathematical model to assist in solving the given problem.
Even though a minor mistake was observed (namely incorrectly jotting down x + y = 5 instead of x + y = 54) in line 6 of learner H's solution (Figure 8), 'severity' thereof is diminished by having written down the correct equation x + y = 54, in line 10 of the calculation. The learner then continued by using elimination together with the effective usage of applicable mathematical procedures and manipulations to obtain the required values of the respective numbers. No effort was made by the learner to reflect on, or check the validity, or correctness of, answers 24 and 30. Learner H did not explicitly state that x and y represented the two unknown numbers, nor which of the variables (x or y) represented the greater number or smaller number. It is rational to accept that variables x and y were allocated to the unknown numerical values as indicated in the constructions of two sets of relationships represented by following the system of linear equations:
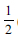 (x + y) = 27 → (x + y) = 54 → (x − y) = 6.
(x + y) = 27 → (x + y) = 54 → (x − y) = 6.
The learner at the beginning attempted to solve the problem by constructing 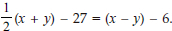 . Then through manipulation he arrived at (x + y) - (x - y) = −6 + 27-1/2. These steps are mathematically incorrect and prevented the learner from obtaining the values of x and y. It seems reasonable to assume that the learner on realising that he was stuck at that point, recalled the procedure to solve a system of simultaneous equations, and consequently proceeded to reflect on the initial set of equations by rewriting it as follows:
. Then through manipulation he arrived at (x + y) - (x - y) = −6 + 27-1/2. These steps are mathematically incorrect and prevented the learner from obtaining the values of x and y. It seems reasonable to assume that the learner on realising that he was stuck at that point, recalled the procedure to solve a system of simultaneous equations, and consequently proceeded to reflect on the initial set of equations by rewriting it as follows:
x + y = 54 ……(1)
x − y = 6 ……(2)
This system unintentionally describes the nature of the mathematical model to be solved to find the two given values described in this problem. The learner refrained from sharing what he was doing in each step. The procedures used to solve for x and y it can be easily identified. In order for the learner to arrive at 2x + 0 = 60 he added equation (1) to equation (2), and solved for x to get x = 30. The equation 30 + y = 54 also indicates that x was replaced by 30 in equation (1), namely x + y = 54. The learner accurately solved 30 + y = 54 to obtain y = 24. The learner concluded by indicating that '∴ x = 30 and y = 24'. All of this demonstrates that the learner possesses the basic knowledge and understanding of how to go about to solving the system of linear equations simultaneously. Like so many other participants this learner shared no evidence that he actually verified and validated his solutions.
Analysis of modelling competencies: Problem 4 in the worksheet
An expected solution for Problem 4 is as follows:
Let the digit in the unit place be x and the digit in the tens place be y. Then x = 3y ………… (1), and the number is 10y + x
The number obtained by reversing the digits is 10x + y.
If 36 is added to the number, digits interchange their places,
Therefore, we have 10y + x + 36 = 10x + y
9x - 9y = 36 → x - y = 4 ……….(2)
Substituting the value of x = 3y in equation (2), we get
3y - y = 4 → 2y = 4 → y = 2
Substituting the value of y = 2 in equation (1), we get
x - 2 = 4 → x = 6
Therefore, the number is 10(2) + 6 = 26
Check: The units digit is 6 and the tens digit is 2. Since the units digit 6 = 3 x 2, it is three times the tens digit which is 2.
Figure 9 depicts that 12 out of 20 learners (60% of the sample) demonstrated level 1 modelling competence, 6 out of 20 learners (30%) demonstrated level 2 competence and 2 out of 20 learners (10%) demonstrated level 3 competence.
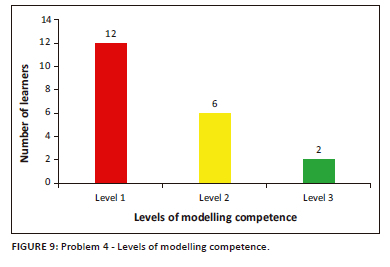
Exemplification of level 1 modelling competence
The majority of learners in the sample, namely 60%, as presented in Figure 9, struggled to make sense of information contained in the problem. Learner 3, in line 1, for instance, simply held on to 36 (which is defined in the problem) without actually sharing a logical reason for doing so, and wrongly judged 2 to be the 'two-digit' number, by finding the difference between 36 and 34. Apparently, the learner upon looking at the statement 'the unit digit is thrice the tens digit' mistakenly subtracted 3 × 10 from 36 (as showed in line 2 in Figure 10), and on top of that also calculated incorrectly by writing '36 = 3 × 10 = 43'. These challenges that learners encountered bear witness to their inabilities to identify numerical values and not recognise quantities related to the problems and their constrained thinking skills. The expressions and relationships they came up with hardly made sense.
Exemplification of level 2 modelling competence
Figure 11 indicates that learner 13 allocated the variable x to the units digit and y to the tens digit as observed in the algebraic representation 'x = 3y' in line 1. By having written down 'x = 3y', he indicates an understanding of the meaning of the given statement: 'In a two-digit number, the unit digit is thrice the tens digit'. In line 2, the learner wrote '= 10y + x', and disregarded the true meaning of the equal sign as 'x = 3y ≠ 10y + x'. This might have been a slip since it is evident in line 3 that the learner actually represented the two-digit number in the form '10y + x'.

In line 3, the learner wrote: '∴ 10y + x + 36 = 10x + y'. Evidently, this skill of successfully building this algebraic linear equation through assigning variables x and y is proof that the learner grasped the problem to the extent of identifying relevant numerical values related to the problem and building meaningful relationships between the variables. The effective construction of a mathematical model reveals the learner's high degree of insight linked to significant features of the problem. Lines 4-8 prove that the learner has an awareness that this particular model may be solved simultaneously by means of the following system of linear equations:
x = 3y ………..(1)
10y + x + 36 = 10x + y ………..(2)
The learner confirms in line 4 that he substitutes x = 3y; however, he does not specifically acknowledge into which equation. There are also no specific details provided of how he arrived at the correct solution, 3y − y = 4 in line 5, through substituting and simplifying. The learner, as indicated in line 6, may have simplified more to obtain y = 2. The learner probably substituted y = 2 into (2) and done some manipulation to obtain x − 2 = 4. This was where the learner ended his engagement with this particular problem, and as a consequence his effort was incomplete, even though he clearly displayed the potential and skills to successfully solve the problem.
Exemplification of level 3 modelling competence
Figure 12 depicts the ability of learner 1 to identify numerical values such as the units and tens digit featured in the problem and expertly allocate designated variables x and y to them. This action enhances the learner toward building an initial algebraic representation of the unknown two-digit number in the form '10x + y'. These steps taken by learner 1 are critical for advancing in constructing a comprehensive mathematical model to obtain the digits that constitute the unknown numerical value. The learner also meaningfully interpreted the significance of the statement 'the unit digit is thrice the tens digit' by means of mathematical symbols and variables to create an algebraic relationship: 'x = 3y' in line 3. This learner obviously understood what was meant by the conditions contained in the statement: 'If 36 is added to the number, the digits interchange their place'. This was evident in their having expressed the resultant two-digit number, if the digits were swapped, properly in the algebraic form as '10y + x'. All of the abovementioned recognised algebraic relationships formed the foundation for the learner to articulate his deep understanding of the conditional statement in line 8, as '10y + x + 36 = 10x + y'. There is no doubt that the latter equation as algebraic representation expresses a critical 'relationship' that represents an integral part of the system of linear equations that portrays what the mathematical model requires in order to solve this problem.
Figure 12 serves as proof that the learner is resourceful and makes satisfactory progress in solving the system of linear equations that follow:
x = 3 ………..(1)
10y + x + 36 = 10x + y ………..(2)
As a consequence of the above, the learner successfully arrived at the correct values for x and y, namely y = 2 and x = 6. This means that the learner demonstrated the required skills to attain the desired mathematical solution by solving the constructed mathematical model properly. To summarise, it is noted that the values y = 2 and x = 6 were properly interpreted within the context of the problem, and in relation to the unknown value given as 10x + y to find 26. No effort was made to verify or to check the validity of the solution in this case.
Discussion of the findings
The findings centre on participating learners' replies that deal with their modelling abilities shown while solving five contextual problems. The discussion is structured in terms of learners' abilities extending through three levels as indicated formerly, namely level 1 (incompetent), level 2 (moderately competent), and level 3 (competent). Figure 13 is a representation of the findings that reveal the majority of participants' (fluctuating from 55% to a maximum of 75%) proficiency to be on level 1. A small percentage (from 20% to 35%) of the participants managed to achieve level 2. Those who performed on level 3 ranged from 10% to 25% through the five problems.
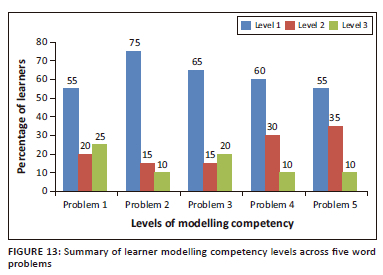
As a rule, those learners new to the process of modelling revealed impaired understanding in making appropriate assumptions in terms of contextual problems, displayed impaired mathematisation skills, or seemed not to possess the ability to construct viable or acceptable models that could be employed as a means to arrive at a solution. These research outcomes show a resemblance to Eric et al.'s (2012) study involving primary 5 learners. They similarly observed that participating learners to a large extent failed to demonstrate modelling proficiency.
Grade 10 participants' problem-solving efforts clearly reflected severe reading and comprehension impairements which hampered understanding and retarded progress or prevented participants from arrving at solutions. This state of affairs was observed in those participants who demonstrated level 1 modelling skills throughout the set of five problems. As illustration, consider the instance (in Problem 1) where five participants could not decipher the relationship between 27 and 6 and the notions of 'sum and difference'. The accompanying mathematical statements from these participants were questionable and indicated improper use of the equal sign. Learner X was obviously unaware that 27 was the correct answer to the addition of the two numbers, and not half of 27. It was also observed that learner X failed to figure out the quantities between which a difference of 6 exists, and as a result came up with an incorrect number sentence, namely 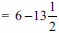 .
.
The apparent inability to understand the message that a problem attempts to convey was generally perceived to be the main stumbling block. This inability to comprehend or make sense was overwhelmingly exhibited by participants' impaired understanding of how a hypothesis may connect to a conclusion in any specified conditional statement through particular problems. To illustrate this, consider the fact that in terms of Problem 2 the majority of participants operating on modelling ability level 1 seemed to reveal limited constructions of the concept of fraction, as they could not assign proper meaning to  . For example, for Problem 2, the conclusion in the conditional statement 'If 1 is added to the numerator and 2 to the denominator the ratio of the numerator to the new denominator is 2:3' has literally been taken to mean the resultant fraction is
. For example, for Problem 2, the conclusion in the conditional statement 'If 1 is added to the numerator and 2 to the denominator the ratio of the numerator to the new denominator is 2:3' has literally been taken to mean the resultant fraction is  rather than realising that the ratio of the numerator to the denominator in the new fraction after adding 1 to the numerator and 2 to the denominator is
rather than realising that the ratio of the numerator to the denominator in the new fraction after adding 1 to the numerator and 2 to the denominator is 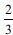 . Furthermore, this group of learners were possibly not conversant with the concept of equivalent fractions, like
. Furthermore, this group of learners were possibly not conversant with the concept of equivalent fractions, like 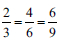 , and hence did not see that the ratio
, and hence did not see that the ratio 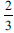 could mean that values of the numerator and denominator are not necessarily 2 and 3 respectively but could also be 4 and 6 or 6 and 9. The possibility exists that all of the confusion and inability to adequately conceptualise to a large extent prevented participants from progressing through the mathematisation stage, with respect to identifying pertinent numerical values and their relations.
could mean that values of the numerator and denominator are not necessarily 2 and 3 respectively but could also be 4 and 6 or 6 and 9. The possibility exists that all of the confusion and inability to adequately conceptualise to a large extent prevented participants from progressing through the mathematisation stage, with respect to identifying pertinent numerical values and their relations.
The problem discussed above, involving learners' apparent impaired comprehension when confronted with conditional statements, is also evident in Problem 3. In this instance a participant, learner 14, for some reason made the second condition the primary focus, and in addition made an incorrect deduction from the statement 'Bob gave Andre R22' that Bob would ostensibly only have R22. Learner 14 furthermore misinterpreted the end part of the second condition, which states 'Andre would then have twice as much as Bob' to imply that Andre possesses 2 × R22 = R44. These learner 14 statements reflect definite shortcomings as far as assigning suitable meaning to the information contained in the problem. Consequently, questionable relationships were inaccurately constructed which also lacked correct assignment and use of the variables.
Likewise, in Problem 4, the majority of participants (12 of 20) experienced similar challenges, namely impaired comprehension, and consequent failure to make sense of the problem. In this illustration, learner 3 erroneously believed 2 to be the 'two-digit' numeral value and deducted it from 36 resulting in a difference of 34. What's more, the participant upon considering the phrase 'the unit digit is thrice the tens digit', wrongly subtracted 3 × 10 from 36 (shown in line 2 of Figure 10). This participant thus also obtained the wrong result through incorrect computation, namely '36 = 3 × 10 = 43'.
Only 55% of the participants made a deliberate effort to attempt Problem 5. Again, these learners showed an incapacity to clearly understand the meaning of the hypothesis and conclusion representing conditional statements. In this particular instance participants simply chose the value 56 that was stated in the conclusion of the first conditional statement (If twice the age of son is added to age of father, the sum is 56) and just deducted it from 82 that appeared in the conclusion of the second conditional statement (But if twice the age of the father is added to the age of son, the sum is 82). These continual or recurring discrepancies characteristic of these participants' efforts clearly indicate an alignment with their (impaired) reading without comprehending the relevant facts offered in the given conditional statements. These tendencies have been exemplified by other participants too, such as learner 7 who seemingly failed to grasp the initial conditional statement 'If twice the age of son is added to age of father, the sum is 56' when stating that 2x + x = 56. In all likelihood, learner 7 misunderstood that the son's age was twice the father's age, and consequently built a relationship containing variable x, which is considered erroneous.
The small number of participants who demonstrated level 2 and level 3 modelling competencies for each of Problems 1-5 appeared to have understood appropriate facets supplied in each of the problems allowing them to mathematise relevant quantities and their relations for each problem. This also enabled these few participants to correspondingly construct meaningful mathematical models represented by a system of linear equations. Participants at level 2, however, apparently did not possess the required abilities to solve the system of linear equations built by them. For example, in respect of Problem 5, learner 15 correctly constructed his system of linear equations 2x + y = 56 and x + 2y = 82 to get 3x + 3y = 138 by means of addition. Unfortunately, he then erroneously simplified it to x + y = 15 and then ceased working. Similarly, learner 11 mistakenly condensed the same system of linear equations 2x + y = 56 and x + 2y = 82 to x + y = 26 instead of −x + y = 26 by means of subtraction and ended abruptly. These chosen strategies indicate a collapse in terms of solving systems of linear equations properly and fully. The sudden endings at particular phases during the calculations again indicate that level 2 participants did not interpret their answers to verify whether such answers were meaningful or not. The few participants who revealed level 3 modelling competencies, however, efficiently solved their systems of linear equations to obtain the precise solutions.
With hindsight, the small number of participants who revealed level 3 abilities by successfully engaging with and solving Problems 1-5 grasped the essence of the problem, identified the crucial and pertinent numerical values, and managed to allocate variables appropriately and in alignment with the 'simultaneous equation' approach. These specific participants built eloquent relationships between the variables as systems of algebraic linear equations for each problem, and solved them accurately. The majority of participants, though, abruptly finished what they were doing once they established the numerical values of variables x and y. Very few participants managed to elucidate the respective values of x and y by reaffirming the meaning assigned within the context of the problem. As illustration, learner 12 in the case of Problem 5 clearly acknowledged that x = 36 is connected to the age of the father and that y = 10 is connected to the age of the son. Learner 1, in a more agreeable way, reflected on his initial assumption that the two-digit number was in the form xy. He also fittingly integrated values y = 2 and x = 6 derived through solving his system of linear equations simultaneously to configure that the two-digit number was equal to 26. In this case the participant exhibited awareness, understanding and an adequate level of explanation and clarification of the solution. Similarly to the majority of participants in this group, however, learner 1 made no effort to verify whether the values of x and y would satisfy the conditional statements governing Problem 4.
In summary, alarmingly many participants operating on the level 1 modelling competency exhibited severe limitations of modelling abilities and their related sub-skills across their responses to the corresponding word problems. Once again, participants' failure to make sense of a problem was observed to be the foremost inhibiting factor preventing participants from: (1) grasping the context or drawing or jotting down whatever was related to the problem, or (2) identifying numerical values as aligned with the problem and assigning variables, or obtaining relations to any mathematical concepts, or (3) mathematising the context to facilitate the construction of mathematical relationships or a mathematical model, or (4) observing that building a system of linear equations, to be solved simultaneously, could enhance solving a given problem. This specific group of participants, upon displaying level 1 modelling competencies (not competently), showed some inability to effectively progress onto the more advanced stages of constructing and solving efficient models.
Those particpants operating on level 2 modelling competency formed a very small percentage of the total sample and were able to read and understand a problem and build a system of linear equations (i.e., build a mathematical model). Unfortunately they did not possess the required mathematical knowledge and skills to explain and successfully solve the systems of linear equations they constructed. Interestingly, this tiny group of participants was adquately skilled in terms of comprehending what the problem confronted them with. They successfully mathematised the context by discussing pertinent mathematical ideas that ultimately related to the mathematical entity represented in the model they constructed. Attempts to mathematise a condition seemed to allow these participants operating on level 2 to succeed in making connections or links between the actual problem and the created mathematical structure of the model. There is no doubt that these particular participants' respective models were characterised by suitable systems of linear equations. Sadly, their failure to solve systems of linear equations using a simultaneous approach prevented them (level 2 modelling competency) from finding workable and sensible solutions to specified problems. It needs to be said also that this group of participants slipped up in terms of verifying or cross-checking the solutions they arrived at.
Only a few participants progressed to or demonstrated level 3 modelling competency. These particular participants progressed effortlessly and persistently through the first three phases of the modelling process, which include making sense of the problem, constructing usable models and solving them. They were also successful in identifying all related numerical values aligned to the problem, variables were appropriately assigned, and relationships meaningfully constructed between generated variables. These participants' mathematical language usage was spot on. They were skilled at using suitable notation, including representations such as diagrams and number sentences. Their abilities to mathematise relevant quantities and their relations were beyond reproach, and as a result they succeeded in building mathematical models represented by systems of two linear equations dealing with two variables (such as t for time and d for distance). The majority of participants operating at level 3 of mathematical modelling appeared not to have verified or inspected the solutions for possible flaws. At least one or two participants took the trouble to interpret their solutions or check if the solutions satisfied the conditions specified at the outset.
Conclusion
A critical finding as far as this study is concerned is many learners' narrow grasp of analysing and making sense of a problem they are confronted with. This degree of incompetence serves as a stumbling block, preventing them from advancing from one stage to the next more advanced stage in the mathematical modelling process, toward the solution. This means participant learners struggled with constructing and solving models, as well as experiencing difficulties interpreting solutions. It emerged that the link between comprehending or grasping what a problem constitutes and solving that problem was quite evident.
One way of addressing learners' inability to fully understand a problem could be to compel learners to relate the problem detail (such as facts) in their own words, and state what was needed to solve the problem successfully. Consequently, clarity of focus in terms of language is a definite requirement for learners to adequately internalise given information or to construct a realistic representation thereof. So, in brief, only once the problem is fully understood can an appropriate solving strategy be decided upon. The latter also positively impacts on how rapidly an outcome is achieved. Ultimately, the importance of fully understanding a particular problem cannot not be over-stressed because of its implications for allowing learners to comment meaningfully on the reasonableness of a solution or answer to a problem (Naidoo et al., 1995). By understanding, learners are encouraged to accept the challenge of solving problems on systems of simultaneous equations, since they find these 'demanding and difficult involving numerous processes' (Ugboduma, 2012, p. 130). With specific reference to simultaneous equations, Johari and Shahrill (2020) mention it to be a challenging topic in school mathematics with which learners normally encounter problems.
Govender (2018), continues to stress that this disposition of frequently failing to make complete sense of what the problem expects of them could have prevented learners in this study from 'making adequate representation of the situation which could help simplify and structure the situation for mathematisation to begin'. The state of impaired reading and conceptualisation skills could be minimised or countered by how lessons were planned and classrooms structured. In this regard, Govender (2018) stresses that lesson design for optimal success in mathematical modelling needs to teach 'reading and understanding of problems [as] part our daily/regular classroom activity'.
In essence, mathematics lessons geared toward the development and enhancement of modelling skills should offer learners ample time and space for scaffolding while working on problems that require mathematisation. Immediate or instantaneous feedback as formative assessment from the teacher is essential. There is no doubt that mathematics teachers need to be adequately equipped through pre-service and in-service training in the design and execution of how to teach modelling effectively.
Acknowledgements
This article is partially based on D.M.'s thesis, entitled 'Mathematical modelling with simultaneous equations - An analysis of Grade 10 learners' modelling competencies', presented in partial fulfilment for the degree of Master's in Mathematics Education, Faculty of Education, University of the Western Cape, with supervisor Prof. R. Govender, in 2020, available here: http://hdl.handle.net/11394/7276.
Competing interests
The authors declares that they have no financial or personal relationships that may have inappropriately influenced them in writing this article.
Authors' contributions
R.G. was the main author who conceptualised, wrote, supervised, and sourced the data. D.M. assisted with the data sourcing.
Ethical considerations
Ethical requirements were adhered to. Permission was sought from the Department of Education and ethical clearance was obtained from the University of Western Cape Ethical Research Committee (HS/16/85). Consent forms were obtained from participating learners and their parents. Participants were informed about the research process that was to be conducted, and given the opportunity to exit the research activities at any stage that they felt uncomfortable.
Funding information
This research received no specific grant from any funding agency in the public, commercial, or not-for-profit sectors.
Data availability
Data sharing is not applicable to this article as no new data were created or analysed in this study.
Disclaimer
The views and opinions expressed in this article are those of the authors and do not necessarily reflect the official policy or position of any affiliated agency of the authors.
References
Araújo, J.D. (2010). The mathematization process as object-oriented actions of a modelling activity system. Bolema - Mathematics Education Bulletin, 64(68), 847-868. https://doi.org/10.1590/1980-4415v34n68a01 [ Links ]
Ärlebäck, J.B. (2010). Mathematical modelling in upper secondary mathematics education in Sweden: A curricula and design study, Unpublished doctoral dissertation, Linköping University. [ Links ]
Bahmaei, F. (2011). Mathematical modelling in primary schools, advantages, and challenges. Journal of Mathematical Modelling and Application, 1(9), 3-13. [ Links ]
Bassanezi, R.C. (1994). Modelling as a teaching-learning strategy. For the Learning of Mathematics, 14(2), 31-35. [ Links ]
Bhardwaj, P. (2019). Types of sampling in research. Journal of the Practice of Cardiovascular Sciences, 5(3), 177-163. [ Links ]
Blomhoj, M. (2003). Developing mathematical modelling competency through problem based project work - Experiences from Roskilde University. IMFUFA, Department of Science, Systems and Models, Roskilde University.
Blomhoj, M., & Jensen, T.H. (2003). Developing mathematical modelling competence: Conceptual clarification and educational planning. Teaching Mathematics and its Applications, 22(3), 123-139. https://doi.org/10.1093/teamat/22.3.123 [ Links ]
Blomhoj, M., & Jensen, T.H. (2006). What's all the fuss about competencies? Experiences with using a competence perspective on mathematics education to develop the teaching of mathematical modelling. In W. Blum, P.L. Galbraith, & M. Niss (Eds.), Modelling and applications in mathematics education (pp. 45-56). Springer.
Blum, W. (2011). Can modelling be taught and learnt? Some answers from empirical research. In G. Kaiser et al. (Eds.), Trends in teaching and learning of mathematical modelling, international perspectives on the teaching and learning of mathematical modelling (pp. 15-30). Springer Science+Business Media.
Blum, W., & Ferri, R.B. (2009). Mathematical modelling: Can it be taught and learnt? Journal of Mathematical Modelling and Application, 1(1), 45-58. [ Links ]
Brady, C. (2018). Modelling and representational imagination. ZDM Mathematics Education, 50, 45-59. https://doi.org/10.1007/s11858-018-0926-4 [ Links ]
Department of Basic Education. (2013). Annual report. Retrieved from https://www.education.gov.za
Department of Basic Education (DBE). (2011). Curriculum and assessment policy statement for further education and training phase grades 10-12: Mathematics. Printing Works.
Department of Basic Education. (2012, December 28). Regulations pertaining to the national curriculum statements grades R - 12. (Government 17 Notice 1114) in Government Gazette No. 36041. Government Printer. Retrieved from http://www.education.gov.za
Doorman, M., Drijvers, P., Dekker, T., Van den Heuvel-Panhuizen, M., De Lange, J., & Wijers, M. (2007). Problem solving as a challenge for mathematics education in The Netherlands. ZDM Mathematics Education, 39, 405-418. https://doi.org/10.1007/s11858-007-0043-2 [ Links ]
Dundar, S., Gokkurt, B., & Soylu, J. (2012). Mathematical modelling at a glance: A theoretical study. Procedia- Social and Behavioral Sciences, 46, 3465-3470. https://doi.org/10.1016/j.sbspro.2012.06.086 [ Links ]
Durandt, R., Blum, W., & Lindl, A. (2021). Fostering mathematical modelling competency of South African engineering students: Which influence does the teaching design have? Educational Studies in Mathematics, 109, 361-381. https://doi.org/10.1007/s10649-021-10068-7 [ Links ]
Drijvers, P., Goddijn, A., & Kindt, M. (2011). Algebra education: Exploring topics and themes. In P. Drijvers (Ed.), Secondary algebra education (pp. 5-26). Sense Publishers.
Epp, S.S. (2011). Variables in mathematics education. In P. Blackburn, H. Van Ditmarsch, M. Manzano & F. Soler-Toscano (Eds.), Tools for teaching logic. Springer Publishing. Retrieved from https://link.springer.com/chapter/10.1007/978-3-642-21350-2_7
Eric, C.C.M., Dawn, N.K.E., Wanty, W., & Seto, C. (2012). Assessment of primary 5 students' mathematical modelling competencies. Journal of Science and Mathematics Education in Southeast Asia, 35(2), 146-178. [ Links ]
Ferri, R.B. (2006). Theoretical and empirical differentiations of phases in the modelling process. ZDM, 38(2), 86-95. https://doi.org/10.1007/BF02655883 [ Links ]
Freudenthal, H. (1968). Why to teach mathematics so as to be useful. Educational Studies in Mathematics, 1, 3-8. https://doi.org/10.1007/BF00426224 [ Links ]
Govender, R. (2018). Analysis of pre-service teachers' mathematical modelling moves on a practical problem. In R. Govender & K. Junqueira (Eds.), Proceedings of the 24th Annual National Congress of the Association for Mathematics Education of South Africa (pp. 189-202). Jojo.
Goffree, F. (1993). Working on mathematics education. Educational Studies in Mathematics, 25(1), 21-49. https://doi.org/10.1007/BF01274100 [ Links ]
Johari, P.M.A.R., & Shahrill, M. (2020). The common errors in the learning of the simultaneous equations. Infinity, 9(2), 263-274. https://doi.org/10.22460/infinity.v9i2.p263-274 [ Links ]
Jorgensen, R. (2014). Inclusive mathematics classrooms. In S. Lerman (Ed.), Encyclopedia of mathematics education (pp. 284-286). Springer. https://doi.org/10.1007/978-94-007-4978-8.
Julie, C., & Mudaly, V. (2007). Mathematical modelling of social issues in school mathematics in South Africa. In W. Blum, P.L. Galbraith, H.W. Henn, & M. Niss (Eds.), Modelling and Applications in Mathematics Education. New ICMI Study Series (vol. 10, pp. 503-510). Springer. https://doi.org/10.1007/978-0-387-29822-1_58
Kieran, C. (2007). Learning and teaching Algebra at the middle school college levels. In F.K.J. Lester (Ed.), Second handbook of research on mathematics teaching and learning (p. 707). New Age Publishing.
Krulik, S., & Rudnick, J.A. (1993). Reasoning and problem solving. A handbook for elementary school teachers. Allyn and Bacon.
Maaß, K. (2006). What are modelling competencies? Zentralblatt fur Didaktik der Mathematik (ZDM): The International Journal on Mathematics Education, 38(2), 113-142. https://doi.org/10.1007/BF02655885 [ Links ]
McMillan, J.H., & Schumacher, S. (2012). Research in education: Evidence based research (1st ed.). Pearson Education.
Muthuri, C.W. (2009). Mathematical models. In K.C. Muir-Leresche & E. Richard Adipala (Eds.), Graduate environmental and agricultural research (GEAR): A guide to effective and relevant graduate research in Africa (2nd ed., pp. 231-241). RUFORUM, Regional Universities Forum for Capacity Building in Agriculture.
Naidoo, A., Smit, S.L., & Van Heerden, J. (1995). Mathematics didacticts theory for primary schools. Shuter & Shooter.
Niss, M. (2003). Mathematical competencies and the learning of mathematics: The Danish KOM project. In A. Gagatsis & S. Papastavridis (Eds.), 3rd Mediterranean Conference on Mathematical Education (pp. 115-124). The Hellenic Mathematical Society.
Niss, M. (2015). Mathematical literacy. In S. Cho (Eds.), The proceedings of the 12th international Congress on mathematical education. Springer. Retrieved from https://link.springer.com/chapter/10.1007/978-3-319-12688-3_31
Nordin, N.H., Tengah, K., Shahrill, M., Tan, A., & Leong, E. (2017). Using visual representations as an alternative in teaching simultaneous equations. Proceeding of the 3rd International Conference on Education, 3, 198-204. https://doi.org/10.17501/icedu.2017.3121 [ Links ]
Oberholzer, I. (1992). Mathematical modelling. In M. Moodley, R.A. Njisane, & N.C. Presmeg (Eds.), Mathematics education for in-service and pre-services teachers (pp. 193-209). Shuter and Shooter.
Pólya, G. (1973). How to solve it: A new aspect of mathematical method (2nd ed.). Princeton University Press.
Schaap, S., Vos, P., & Goedhart, M. (2011). Students overcoming blockages while building a mathematical model: Exploring a framework. In G. Kaiser, W. Blum, R. Borromeo Ferri & G. Stillman (Eds.), Trends in teaching and learning of mathematical modelling. International perspectives on the teaching and learning of mathematical modelling (vol 1). Springer. https://doi.org/10.1007/978-94-007-0910-2_15
Schoenfeld, A.H. (1992). Learning to think mathematically: Problem solving, metacognition, and sense-making in mathematics. In O.A. Grows (Ed.), Handbook for research on mathematics teaching and learning (pp. 334-370). MacMillan.
Seifi, M., Haghverdi, M., & Azizmohamadi, F. (2012). Recognition of students' difficulties in solving mathematical word problems from the viewpoint of teachers. Journal of Basic and Applied Scientific Research, 3, 2923-2928. [ Links ]
Sepeng, P., & Madzorera, A. (2014). Sources of difficulty in comprehending and solving mathematical word problems. International Journal of Educational Sciences, 6(2), 217-225. https://doi.org/10.1080/09751122.2014.11890134 [ Links ]
Tong, D.H., Loc, N.P., Uyen, B.P. Tho, C., & Giang, L.T. (2019). Developing the competency of mathematical modelling: A case study of teaching the cosine and sine theorems. International Journal of Learning, Teaching and Educational Research, 18(11), 18-37. https://doi.org/10.26803/ijlter.18.11.2 [ Links ]
Ugboduma, S.O. (2006). Effective methods of teaching mathematics as it affects Nigerian secondary schools. Journal of Knowledge Review, 12(1), 118-124. https://doi.org/10.4314/gjedr.v11i2.8 [ Links ]
Ugboduma, S.O. (2012). Students' preference of method of solving simultaneous equations. Global Journal of Educational Research, 11(2), 129-136. http://doi.org/10.4314/gjedr.v11i2.8 [ Links ]
Usiskin, Z. (1999). Conceptions of school algebra and uses of variables. In B. Moses (Ed.), Algebraic thinking, grades K-12: Readings from NCTM's school-based journals and other publications (pp. 7-13). National Council of Teachers of Mathematics.
Western Cape Government. (2023). 2022 systemic test results show interventions are working. Retrieved from https://www.westerncape.gov.za/news/2022-systemic-test-results-show-interventions-are-working
Yunus, D.H.R.P.H., Shahrill, M., Abdullah, N.A., & Tan, A. (2016). Teaching by telling: Investigating the teaching and learning of solving simultaneous linear equations. Advanced Science Letters, 22(5/6), 1551-1555. https://doi.org/10.1166/asl.2016.6676 [ Links ]
 Correspondence:
Correspondence:
Rajendran Govender
editor@pythagoras.org.za
Received: 19 Oct. 2022
Accepted: 15 Sept. 2023
Published: 08 Dec. 2023














