Services on Demand
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
Journal of the Southern African Institute of Mining and Metallurgy
On-line version ISSN 2411-9717
Print version ISSN 2225-6253
J. S. Afr. Inst. Min. Metall. vol.116 n.3 Johannesburg Mar. 2016
http://dx.doi.org/10.17159/2411-9717/2016/v116n3a11
PAPER OF GENERAL INTEREST
Critique of the South African squat coal pillar strength formula
M. Mathey; J.N. van der Merwe
School of Mining Engineering, University of the Witwatersrand, Johannesburg
SYNOPSIS
The South African squat coal pillar strength formula, developed by researchers from the Chamber of Mines Research Organization in the 1980s, predicts an exponential increase in coal pillar strength once a critical width-to-height ratio of 5 is exceeded. The arguments that have been proposed in favour of this formula are discussed critically in this paper.
Field experience with squat pillars in the USA and evidence from published physical, analytical, and numerical model pillar studies corroborate the fact that a squat effect is unlikely to occur in coal pillars at width-to-height ratios less than 10. Furthermore, an exponential increase in peak strength of coal pillars does not exist. An alternative design criterion for squat pillars in South Africa is therefore suggested.
Keywords: squat pillars, coal pillar strength, bord-and-pillar mining.
Introduction
Five decades of coal pillar research in South Africa have produced a wealth of information on the mechanisms contributing to the strength and failure of in-situ coal pillars and accompanying phenomena. The relevant knowledge was sourced from, and for, a South African coal mining environment that remained largely unchanged in the second half of the 20th century. The depth of mining seldom exceeded 250 m, with mined seam thicknesses averaging 3 m and typical pillar width-to-height ratios (w/h) of 3-4.
It is therefore not surprising that comparatively little research has been directed at the prediction of coal pillar performance in deeper deposits, where squat pillars of larger width-to-height ratios will be required to support the overlying strata. However, a thorough understanding of squat pillar performance will be necessary should the remaining deep coal deposits of the country be extracted in future, for instance in the Waterberg or Ermelo coalfields.
A squat coal pillar strength formula has already been proposed in South Africa. The origin of this formula will be discussed in some detail in the following sections and its appropriateness will be critically reviewed against a great amount of evidence from relevant squat coal pillar research conducted internationally.
Squat pillar strength in South Africa
The background to the South African squat coal pillar strength formula is provided by the original work of Salamon and Munro (1967), who predicted the strength of slender pillars of width-to-height ratios of up to 3.6 to be:
Strength = 7.2 w0-46/h0.66 MPa [1]
The formula implies that for a constant pillar height h and increasing pillar width w (i.e. increasing width-to-height ratio), the strength of pillars increases regressively.
Salamon and Oravecz (1973) commented that Equation [1] 'underestimates the strength of pillars when [the width-to-height ratio] is greater than 5 or 6. There is some evidence that when pillars have a width-height ratio exceeding, say, 10-12, they do not fail under any practically possible load'. Salamon (1982) proposed a separate strength formula for squat pillars, which allowed for a rapid increase in pillar strength once a critical width-to-height ratio is exceeded:

where R0 is the critical width-to-height ratio for the onset of squat pillar strength, R is the width-to-height ratio of the squat pillar, V the pillar volume, and e a parameter which controls the rate of strength increase with increasing R in squat pillars.
Salamon and Wagner (1985) subsequently published further explanations as to the background of Equation [2]. They thought to find evidence in theoretical and experimental studies of cohesionless, granular materials, as well as in compression tests on sandstone model pillars, 'that the strength of squat pillars increases very rapidly, perhaps even exponentially, with increasing width-to-height ratio, once a certain value of the ratio has been exceeded' (Salamon and Wagner, 1985). It was suggested that R0 = 5 would perhaps be a reasonable estimate of the critical width-to-height ratio for the onset of squat pillar strength, and a rate of strength increase of e = 2.5 was selected to design experimental panels in collieries.
Equation [2] predicts significant increases in the strength of squat coal pillars as compared to the original Salamon and Munro (1967) strength formula, which is demonstrated in Figure 1. Consequently, it improves the extraction rates for bord-and-pillar mining layouts at greater depths.
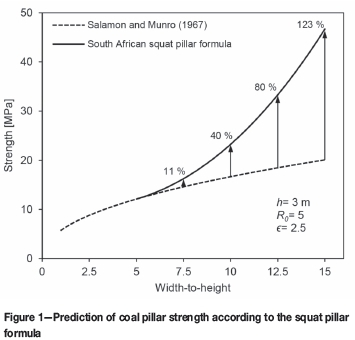
Madden (1990) undertook research to substantiate Equation [2] with further evidence. He reported on an extensive laboratory testing programme, in which five sets of sandstone model pillars with sizes ranging between 24-100 mm and width-to-height ratios of 1-8 were loaded in compression between steel platens. The results were such that up to w/h = 5 or 6, the strength of the model pillars increased approximately linearly, and thereafter more rapidly with further increasing width-to-height ratio. Madden's laboratory test results will be discussed in further detail in a later section.
Madden (1990, 1991) also investigated the performance of squat coal pillars at Piet Retief and Longridge collieries in KwaZulu-Natal. By means of boreholes drilled horizontally through the pillars, he established the maximum depth to which stress-related fractures penetrated into the pillars. He concluded that the fracture penetration depth was limited to the pillar skin only, and the large intact cores of those pillars suggested that the overall strength of the pillar would be significantly higher than predicted by the formula of Salamon and Munro (1967). This was thought to substantiate the validity of the squat pillar strength formula. Madden (1991) reported further that extensive field trials at Hlobane and Piet Retief collieries had shown that the squat pillar formula gives stable pillar dimensions. However, more accurate estimates of the critical parameters R0and e could not be established from this research.
During the past 30 years since the introduction of the squat pillar strength formula, no pillar with w/h > 5 has ever been observed to collapse in South Africa. The largest collapsed width-to-height ratios reported in the literature are 3.6 and 4.3 in coalfields of normal and weak coal pillar strength respectively (Van der Merwe and Mathey, 2013b).
However, the absence of squat pillar collapses does not necessarily confirm the validity of the squat pillar formula. A great number of squat pillars in South African collieries are simply overdesigned and do not fail due to the very high safety factors employed. Figure 2 plots the safety factors of all 84 squat pillar cases stored within the South African databases (Van der Merwe and Mathey, 2013b). The strength has been conservatively calculated with Equation [1] and would be even greater if calculated according to Equation [2]. Note also that none of the squat pillars were loaded beyond 11 MPa.

The strength of coal pillars revisited
The assumption of an exponential increase in strength of squat pillars with w/h > 5 is certainly unique and not free from reasonable doubt. To the contrary, there is substantial evidence available from field observations on squat pillars in-situ and from model pillar studies that argue against an exponential strength increase. This evidence will be presented in the following sections of this paper.
Beforehand, it may be advantageous to begin the critique of the South African squat pillar formula with a detailed review of the arguments that have been proposed in its favour. These have been outlined in the previous section and may be summarised as follows. Firstly, it has been said that the strength of squat pillars in collieries of KwaZulu-Natal appears to be higher than predicted by the original Salamon and Munro (1967) formula. Secondly, studies of model pillars consisting of cohesionless materials or intact rock materials other than coal have indicated a rapid strength increase above a width-to-height ratio of 5. And thirdly, pillars with w/h = 10 or 12 have been observed to withstand any practical load, i.e. they do not fail. The following sub-sections will provide alternative explanations for these observations, from which it will be seen that an exponential strength increase in squat coal pillars is not necessarily evident.
The strength of squat pillars in KwaZulu-Natal appears to be greater than predicted by the Salamon and Munro (1967) formula
The Salamon and Munro (1967) pillar strength formula, and any subsequent update of the same (Madden, 1991; Van der Merwe, 2003; Salamon, Canbulat, and Ryder, 2006; Van der Merwe and Mathey, 2013c), do not represent the actual strength of coal pillars in South Africa. They merely predict the average strength of a specific group of coal pillars, namely those that have collapsed. The advantage of these empirical formulae is that they are very useful as design guidelines to prevent further collapses. However, they do not necessarily predict the actual strength of any given coal pillar.
There is sufficient evidence to assume that the actual strength of coal pillars may be highly variable. Differences in pillar strength between coalfields (Van der Merwe and Mathey, 2013b, 2013c) and groups of seams (Salamon, Canbulat, and Ryder, 2006) have already been proposed, based on the statistical characteristics of collapse cases. But even within areas with the same failure characteristics, it is estimated that only about 10 % of all pillars with a predicted safety factor of unity actually collapse (Van der Merwe and Mathey, 2013a). This in turn suggests that the average strength of coal pillars may be higher than that assumed by the Salamon and Munro (1967) formula.
A good idea of the possible variation in the actual coal pillar strength can be gained from the compression tests on large-scale model pillars conducted at Witbank, Usutu, and New Largo collieries (Bieniawski, 1968a; Wagner, 1974; Van Heerden, 1975). The corresponding pillar strength equations are reproduced in Figure 3. Van Heerden (1975) in particular undertook great efforts to produce a stress environment in his model pillars, which resembled those of full-size mine pillars. The result of his tests at New Largo colliery (Figure 3) suggest that the site-specific strength of coal is about three times higher than predicted by the back-analysis of collapse cases (Equation [1]).

In light of the above, it is not surprising that the inferred strength of partially fractured squat pillars in collieries of KwaZulu-Natal appeared to be higher than the strength predicted by the Salamon and Munro (1967) formula. The obvious conclusion from this observation, however, is not that there must have been some kind of squat effect that accounts for the discrepancy. It is rather that the site-specific strength of the investigated coal pillars may simply be different from the prediction made by a formula that is derived from a different coal mining environment. Madden's observations on sidewall fracturing in squat pillars could have been an argument for an increased squat pillar strength only if the validity of the Salamon and Munro formula (1967) for the relevant collieries had first been established for fracture observations in slender pillars.
Evidence from compression tests on model pillars designed from rock materials other than coal
One may distinguish two different failure modes in pillars (Figure 4). Firstly, brittle failure, which has been observed for mine pillars in South Africa up to width-to-height ratios of at least 4. Brittle pillars exhibit a distinct peak strength σρ and a subsequent strength drop to a residual level σr, if additional strain is imposed on the pillar. The failure process is associated with an abrupt or gradual loss of cohesion of the pillar material.
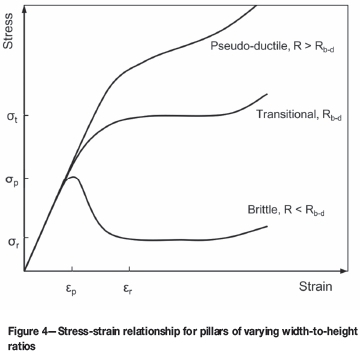
The second category is a quasi-ductile failure mode. Here, the pillar may also lose its cohesion entirely within the failure process, but it maintains or even increases its load-bearing capacity with increasing strain (Figure 4). This failure mode can occur only in pillars with sufficiently large width-to-height ratios, which allow high lateral confinement stresses to be generated within the fractured pillar. While the load-bearing capacity of brittle pillars is dominated by the cohesive strength of the material, pseudo-ductile pillars obtain their seemingly unlimited load-bearing capacity from the frictional shear resistance of the fractured material.
The concept of two different failure modes implies that a critical width-to-height ratio Rb-d exists, at which brittle failure transits into pseudo-ductile failure. The stress-strain behaviour of such a transitional pillar is depicted in Figure 4.
It is obvious that a peak pillar strength criterion such as Equations [1] and [2] can be meaningful only for pillars that fail in a brittle manner. Pillars that perform in a quasi-ductile manner do not exhibit a peak strength, nor do they pose the risk of abrupt failures, load-shedding, and pillar runs in panels. However, they may allow undue deformations to take place in the surrounding strata, which contributes to the deterioration of ground conditions. A strain-based design method, such as the ground-response curves for pillar-strata systems (Esterhuizen et al., 2010b) appears to be most suitable for such mining environments.
However, for the development of appropriate peak strength design criteria for brittle pillars it is necessary to identify the critical width-to-height ratio Rb-d at which brittle-ductile transition occurs in pillars, and how the peak strength develops in brittle pillars over the full range of 1 < R < Rb-d.
Model pillars that consist of cohesionless material (e.g. a pile of gravel) have been used by Salamon and Wagner (1985) to argue in favour of the exponentially increasing strength of squat pillars. Such cohesionless models are, however, of little use in this regard, as they resemble mine pillars that are already fully crushed. Therefore, they can only simulate the performance of pillars that are in a state of residual strength. From a practical perspective, such crushed pillars would already have undergone substantial deformation and the entries would already been lost.
In the past, a large number of laboratory compression tests have been conducted to observe failure modes and strength trends in model pillars. These tests highlight significant differences between model pillars designed from rock materials (which have been used to argue in favour of the current South African squat coal pillar formula) and those designed from intact coal materials.
Laboratory tests on rock model pillars
Bieniawski (1968b) published the results of compression tests on sandstone model pillars which showed that the relationship between strength and the width-to-height ratio increases linearly up to w/h = 5. Further tests at w/h = 10 demonstrated that a model pillar of that size could not be broken even at very high loads.
Cruise (1969) also reported on a testing programme involving sandstone model pillars, for which he observed an upward curving peak strength trend for pillar width-to-height ratios between 1 and 6.7. He found that the trend could be best described by a polynomial curve.
Bieniawski and Van Heerden (1975) presented the results of tests on sandstone model pillars, which again showed a linear relationship between the strength and width-to-height ratios up to w/h = 4. At width-to-height ratios of 5, 6, and 7.5, the strength of specimens was markedly higher than predicted by the trend for the more slender pillars.
The tests on sandstone model pillars conducted by Madden (1990) showed a linear strength increase for width-to-height ratios of up to 5 or 6, at which point brittle-ductile transition occurred in the specimens. The rapid increase in strength for width-to-height ratios greater than 6, which has been reported from Madden's tests, therefore does not refer to an increase in (brittle) peak strength of the model pillars, but to a pseudo-ductile behaviour of the pillars. The onset of brittle-ductile transition at 5 or 6 may also explain why Bieniawski (1968b) was not able to crush a sandstone model pillar of width-to-height of 10. Yet this observation is in conflict with the peak strength values reported for sandstone model pillars by Bieniawski and Van Heerden (1975).
York et al. (1998) reported on compression tests on Merensky Reef model pillars with width-to-height ratios of up to 10. The strength of pillars in the range of 1-6 was found to increase linearly with increasing width-to-height ratio. The test results for higher width-to-height ratios were not reported.
The reviewed tests on rock model pillars agree that the relationship between the strength of pillars and width-to-height ratio for w/h values of up to 5 or 6 may be expressed by a single trend. This trend is linear in most cases. The finding of a critical width-to-height ratio above which pillars start behaving markedly differently may indeed highlight the need for a separate squat pillar design criterion for rock materials. However, the results are inconclusive for the question as to whether squat rock pillars experience a brittle-ductile transition or a more rapid increase in brittle peak strength.
Laboratory tests on coal model pillars
The performance of coal model pillars has been studied in numerous laboratory investigations. Holland (1942) reported on an extensive laboratory testing programme in which coal specimens from different coal seams in West Virginia, USA, were tested at w/h ratios between 1 and 12. He described the results to be very erratic in general, but demonstrated that a linear or regressive increase in specimen strength up to a w/h ratio of 8 fitted the average data well.
However, Holland also noted that some specimens did not fail abruptly. He stated that for these outliers 'there was no point during the application of the load when it could be definitely stated that failure occurred. The bending of tool-steel bearing plates, denting of soft-steel bearing plates, and the distinct imprint of the round hole on the coal specimen suggest that the coal was forced into the plastic state' (Holland, 1942). Yet, upon examination of those specimens it was discovered that the specimens were very fragile and exhibited shear surfaces when broken.
The phenomena described by Holland are exactly those that are associated with the brittle-ductile transition in pillars. In Holland's tests they occurred only for some specimens at w/h ratios between 5 and 12. Holland reasoned that the critical w/h ratio for the transition from abrupt failure to failure through flow or squeezing may be influenced by the generic strength of the coals. Even though not fully conclusive, his tests indicated that the stronger the coal, the higher the critical w/h ratio for the occurrence of flow in the model pillars. In conclusion, Holland therefore commented that 'if these results can be applied to coal-mine pillars, the possibility is indicated that the stronger the coal is on a mine pillar, the wider the pillar must be relative to its height to prevent abrupt failure' (Holland, 1942).
Meikle and Holland (1965) investigated the influence of the contact friction angle between the coal model pillars and the loading platens on the strength of pillars. The study focused on specimens with w/h ratios between 4 and 8. In general it was found that the stronger the interface friction, the higher the strength of pillars at a given width-to-height ratio. However, it was observed that the relationship between specimen strength and the width-to-height ratio increased only regressively, irrespective of the interface friction angle.
The results of Meikle and Holland's tests, together with the results from other published coal model pillar experiments discussed in the following paragraphs, are plotted in Figure 5. It should be noted that for the sake of comparison, all different test results have been normalized to give the same strength for a pillar of w/h = 5. The individual strength trends, which may indicate possible squat effects in the tests, remain unaffected by the normalization. In the study of Meikle and Holland (1965), a squat effect in the form of an exponential strength increase or the brittle-ductile transition was not observed for model pillars with w/h < 8.
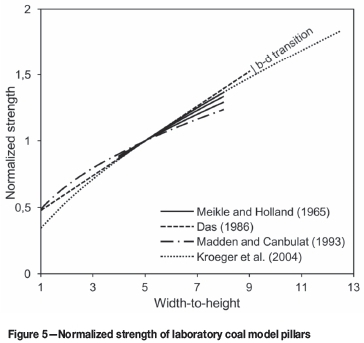
A similar laboratory testing programme was subsequently carried out by Khair (1994) in the USA, who found that the relationship between the strength and shape of coal model pillars with w/h = 4-8 could be expressed by a linear equation for each selected contact friction angle. Again, a squat effect was not observed.
Kroeger, Roethe and Li (2004) also performed compression tests on model coal pillars from different seams in Illinois, USA. They found that the relationship between strength and width-to-height ratio of the specimens can be expressed as a regressively increasing curve for the entire range of w/h = 1-12. The trend for the Murphysboro seam is reproduced in Figure 5. A squat effect was not observed.
In India, Das (1986) tested coal specimens from five different seams at w/h ratios of up to 13.5. He observed that brittle-ductile transition occurred in specimens at very large w/h ratios of around 10. A squat effect in the form of a progressive strength increase is not discernible from his data. The average strength versus width-to-height relationship of specimens from all seams follows a linear trend for w/h rations between 1 and 10, as shown in Figure 5.
In South Africa, Madden and Canbulat (1995) conducted a comprehensive testing programme with more than 900 model pillars of different sizes between 25-300 mm and with w/h ratios between 1-8. Coal samples were sourced from 11 collieries in different coalfields. The strengths of all the model pillars were analysed statistically, and it was found that the following equation provided an adequate fit to the data:
Strength = kw0.139/h0.449 MPa [3]
where k is a strength coefficient, and w and h the specimen width and height in metres. Equation [3] is plotted in Figure 5 in its empirical range, using the average strength factor k = 15.83 MPa for all coals used in the study of Madden and Canbulat (1995), and a specimen width of 100 mm. It should be noted that Equation [3] describes a regressively increasing relationship between strength and the width-to-height ratio of coal model pillars. Neither an exponential increase in strength nor strain-hardening could be identified conclusively in the tested specimens up to w/h = 8.
It is evident from this summary that coal model pillars behave very differently to rock model pillars. The relationship between strength and shape follows a single linearly or regressively increasing trend up to width-to-height ratios of at least 8, in some cases even up to 12, before the brittle-ductile transition can occur. An exponential strength increase has also not been observed for coal model pillars. This raises considerable doubt as to the validity of the South African squat coal pillar formula (Equation [2]). The adoption of the critical width-to-height ratio of 5 for squat effects in coal pillars appears to have been based solely on experience with rock materials, with the assumption that coal behaves similarly. However, the evidence indicates that coal does not behave like the rock samples tested.
Pillars with width-to-height ratios of 10 or 12 do not fail under any practical load
Salamon and Oravecz (1973) stated that coal pillars with very large width-to-height ratios of 10 or 12 do not fail under any practical load. This observation, which has also been made by other researchers (without defining what this practical load would be), initially sparked the idea that squat pillars increase their strength more rapidly than the more slender coal pillars. However, the evidence provided in the previous sub-section strongly suggests that the phenomenon of an apparently unlimited load-bearing capacity of very squat pillars is linked to the brittle-ductile transition in pillars rather than to an exponentially increasing peak strength.
It has thus been demonstrated that not a single piece of evidence exists that unambiguously substantiates the correctness of the South African squat coal pillar formula. The following section will describe different experiences with squat coal pillar strength prediction and design.
Experience and predictions of squat pillar strength internationally
The questions of squat coal pillar strength and coal pillar design at depth have been addressed by various researchers internationally. In Australia, where the strength of slender coal pillars has also been determined from back-calculation of stable and collapsed cases (Salamon et al., 1996), Salamon's suggestion of an exponential increase in squat pillar strength has been adopted without further investigations. Equation [2] has only been modified (Galvin and Hebblewhite, 1995) to meet with the empirical strength equation for slender pillars in Australia at the critical width-to-height ratio of R0 = 5. The exponential rate of strength increase is the same as in South Africa with e = 2.5.
A unique approach to pillar design at depth was pursued by Sheorey et al. (1987) in India, in that a strength formula was proposed that accounts for the influence of virgin stress conditions on the load-bearing capacity of the pillar. The fundamental assumption behind coal pillar strength at depth was that a pillar may be able to retain some of the original horizontal confining stress existing in the coal prior to excavation, depending on its width-to-height ratio and its contact conditions with the surrounding strata. Therefore, with increasing depth, the pillar confinement and vertical load-bearing capacity should increase. The latest available update of the formula, Equation [4], was provided by Sheorey (1992):

where σcis the compressive strength of 2.5 cm cubes of coal in the laboratory, and all other dimensions (w, h, and H) are in metres. Evidence from failed and stable cases in India suggested that Equation [4] was suitable for design of pillars with width-to-height ratios up to 6.7.
In the USA, more detailed insights into the strength and stability of coal pillars with dimensions far in excess of w/h = 5 have been gained. These will be discussed in the following sections.
Evidence from in situ experience
Bieniawski (1992) reviewed a number of empirical coal pillar strength equations from different researchers and compared their performance to the in situ strength of pillars in the USA. He emphasized the suitability of an empirical pillar strength equation that he had derived from the in-situ compression tests in South Africa (Bieniawski and Van Heerden, 1975):

Bieniawski (1992) explains that 'although the original in situ test data ... were based on pillar width-to-height ratios up to 3.4, when applied to full-size coal pillars ... the pillar strength formula given by Equation [5] was found applicable even for pillar width-to-height ratios of up to 12'. The strength trend predicted by Equation [4] for the Pittsburgh seam in the USA is reproduced in Figure 6. It should be noted that Equation [5] predicts a very similar rate of strength increase for pillars as the formula derived by Van der Merwe and Mathey (2013c) for collapsed coal pillars in South Africa, based on the overlap reduction (OR) technique.

Mark (2000) also reviewed his experience with coal pillars in the USA and came to the conclusion that for pillar w/h ratios up to 8, empirical strength formulae were 'reasonably accurate' (Mark, 2000). A further important observation was that abrupt failure occurred only for pillars with w/h up to 3, while 'squeezing' was the predominant failure mode in the interval of 4 < w/h < 8. Squat pillars were those 'which can carry very large loads and are strain-hardening, and which are dominated by entry failure (roof, rib and floor) and by coal bumps' (Mark, 2000). This typically occurred at pillar w/h ratios greater than 10. Mark's observation on in situ squat pillars appear to confirm the trends observed in laboratory coal model pillar tests.
Maleki (1992) reported that in the USA he had observed squat pillars with width-to-height ratios up to 15 to fail underload. In back-calculating the average peak vertical stresses on collapsed pillars from seven coal seams and eight collieries by means of empirical and numerical analysis as well as stress measurements, he established strength versus width-to-height curves for coal pillars far into the squat range. In his analysis of pillar failures, he distinguished the confinement-controlled pillar collapses in competent geological environments from those where the failure mechanism appeared to be structurally controlled, i.e. where failure was aided by persistent cleats and in-seam contact planes. He proposed two strength equations:
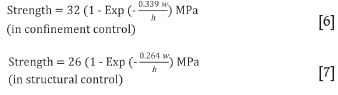
It should be noted that these equations describe a regressive strength increase with increasing width-to-height ratio, which levels off at maximum limiting strength values of 32 MPa and 26 MPa respectively. These maximum values are approached for pillars with width-to-height ratios between 10 and 15. Maleki (1992) states that above these limits, stability problems may occur as a result of failures in roof, seam, and floor. Equation [6] is reproduced in Figure 6.
Indications from analytical models
A number of analytical pillar models have been proposed in the past decades, e.g. (Wilson, 1981; Barron and Pen, 1992; Salamon, 1992; Napier and Malan, 2007). In two cases, the developers have applied their models to the prediction of squat coal pillar performance.
Barron and Pen (1992) developed a model that uses the Hoek-Brown failure criterion to describe the intact and residual strengths of the coal. The criterion is modified to allow brittle-ductile transition to occur in zones of high lateral confinement within the model pillar. The strata surrounding the pillar are assumed to be elastic and infinitely stiff.
Barron and Pen (1992) applied this model to the prediction of squat pillar strength in the Witbank coalfield. It should be noted that the results did not show an exponential increase in strength, but rather suggested an overall regressive increase in pillar strength between width-to-height ratios of 5 and 20. However, for width-to-height ratios of less than 12, the predicted strength was higher than that predicted by the South African squat coal pillar formula (Figure 6).
Salamon (1992) proposed a very comprehensive analytical coal pillar model in which the deformation of a laminated rock mass surrounding the pillar is explicitly taken into account. Salamon et al. (2003) applied this model to the prediction of the strength of three coal pillars with width-to-height ratios of 3, 5, and 10. The results are reproduced in Figure 6, from which it will be seen that only a regressively increasing trend between strength and the width-to-height ratio of coal pillars is indicated.
The magnitude of strength and the rates of strength increase are predicted to be significantly lower than those in the Barron and Pen model. However, both models agree that an exponential increase in peak pillar strength does not occur.
Indications from numerical models
Substantial progress has been made with regard to an understanding of the various factors that contribute to the strength and stability of coal pillars, due to the application of numerical modelling techniques. Some of these findings are particularly relevant for squat coal pillars:
It has been found that the adverse influence of joints on the strength of coal pillars may vanish for pillar width-to-height ratios greater than 6 or 7 (Esterhuizen, 2000). Rock partings in the coal seam can have either a strengthening or weakening influence on pillars, depending on the competence of the parting (Su and Hasenfus, 1999). The seam strength itself, however, may have a negligible impact on the performance of pillars with squat dimensions. The competence of the surrounding rock mass appears to be more important: weak floor strata, for instance, can decrease the ultimate pillar strength by as much as 50 % (Su and Hasenfus, 1999). Also, the cohesive strength of the pillar-strata interface may considerably influence the critical width-to-height ratio for occurrence of brittle-ductile transition in pillars (Lu et al., 2008).
Results from numerical models can give only qualitative insight into the role of different factors that influence pillar strength, unless some form of calibration of the model is conducted. However, the choice of criteria for the model calibration may influence the results dramatically.
For instance, et al. (2010) calibrated coal pillar models against the empirical peak strength criterion for the combined South African and Australian coal pillar databases (Galvin, Hebblewhite, and Salamon, 1999). The extrapolation of the models into the squat range predicted that brittle-ductile transition occurred in pillars at w/h ratios of between 5 and 6.7.
Esterhuizen et al. (2010a) calibrated numerical coal pillar models against Bieniawski's linear strength formula (Equation [4]) and measured stress profiles for in-situ pillar ribs. The extrapolation of the models to greater width-to-height ratios predicted that brittle-ductile transition occurred in pillars at around w/h = 8. A progressive strength increase was not observed.
Tesarik et al. (2013) calibrated models against one pillar stress-strain curve that was obtained by Van Heerden (1975) in his in situ testing programme. The idea behind this calibration procedure was to incorporate information on peak strength, residual strength, and the gradual softening of pillars after fracturing. The calibrated model was extrapolated to larger width-to-height ratios, assuming that the strata surrounding the pillars remained elastic. Tesarik et al. (2013) observed that the strength of their coal model pillars increased regressively up to w/h = 16, when brittle-ductile transition finally occurred. The strength trend is plotted in Figure 6 and it will be seen that there is good agreement with the trend predicted by the Van der Merwe and Mathey (2013c) formula, which was derived from collapsed and stable cases based on the maximum likelihood method (MLM).
It is obvious from the above that the numerical prediction of squat pillar performance is very sensitive towards the selected calibration procedure. There is no agreement on the point of brittle-ductile transition in pillars. However, all presented coal pillar models agree on the fact that a progressive increase in peak strength cannot occur.
Conclusions
The South African squat pillar strength formula predicts an exponential increase in strength for pillar width-to-height ratios of greater than 5. Three major arguments for the South African squat coal pillar strength formula were proposed by Salamon and Wagner (1985):
> The observation that pillars of w/h = 10-12 do not collapse under any practical load
> Theoretical and experimental studies on model pillars consisting of materials other than intact coal had indicated a rapid strength increase above w/h = 5
> In situ observations in collieries in KwaZulu-Natal suggested that squat pillars performed better than expected from the original Salamon and Munro (1967) formula.
It has been argued in this paper that none of the above observations is actually capable of substantiating the exponential nature of the South African squat pillar formula:
Firstly, the very high load-bearing capacity of pillars with w/h ratios of 10 or 12 can be explained more plausibly by the brittle-ductile transition in pillars, and not by an exponentially increased peak strength.
Secondly, laboratory tests on coal model pillars unambiguously agree that the peak strength increases only linearly or regressively for this material until the brittle-ductile transition occurs. There is a great amount of evidence that brittle-ductile transition does not occur in coal specimens with w/h ratios smaller than 8. Also, the brittle-ductile transition does not necessarily occur in coal specimens up to w/h = 13, even though it has been observed in tests on Indian coals to occur at w/h = 10. The phenomena accompanying strength and failure in coal model pillars are therefore appreciably different from those occurring in rock model pillars, for which higher rates of strength increase and an early brittle-ductile transition have indeed been observed by some researchers.
Thirdly, it has been argued that empirical pillar strength formulae that are based on collapse cannot reliably predict the actual strength of any given coal pillar. Therefore a divergent strength of pillars in the squat range does not necessarily justify a squat effect.
To date, no squat pillar has ever been observed to collapse in South Africa. This is because squat coal pillars are designed with very high safety factors. The absence of collapse cases complicates the task of finding a more appropriate design criterion for such structures in the local coalfields. However, a wealth of information is already available from international field experience and analytical and numerical models, which can give qualitative insight into the expected behaviour of squat pillars.
Experience with failed squat pillars in the USA suggests that empirical design formulae, which are derived from large-scale compression tests or from back-calculation of collapsed slender pillars (w/h < 5), may still be reasonably accurate when extrapolated to larger width-to-height ratios of up to 8 or 12. There is even some evidence that a maximum limiting strength may exist for coal pillars, which strongly opposes the South African assumption of an exponential strength increase.
Likewise, the majority of published analytical and numerical coal pillar models agree on the point that the peak strength of coal pillars increases only regressively with increasing width-to-height ratio, until the brittle-ductile occurs. This phenomenon, however, is likely to occur only at very large pillar width-to-height ratios of around 10.
The evidence presented from field experience, laboratory tests, and numerical and analytical models therefore corroborates the conclusion that a progressive increase in coal pillar strength for width-to-height ratios greater than 5 does not exist. Consequently, the South African squat coal pillar formula (Equation [2]) is misleading from a mechanical point of view and must be replaced by a more appropriate design criterion.
Implications for squat pillar design in South Africa
The determination of a more appropriate design criterion is complicated by the fact that no experience with failed squat pillars in South Africa is available so far. Therefore we can currently only estimate a more suitable design criterion based on the international experience outlined in this paper. The following deductions may be made in this regard:
> The empirical coal pillar strength formulae, derived from back-analysis of collapse cases or from in situ compression tests in South Africa, may be extrapolated into the squat pillar range up to w/h = 10. Pillars with width-to-height ratios greater than 10 may perform in a pseudo-ductile manner without exhibiting an ultimate peak strength. For these pseudo-ductile pillars, a strain-based failure criterion is required to limit undue deformations of the pillar-strata-systems
> Since it has become customary in South Africa to base pillar design on experience with failed cases rather than on in situ compression tests, it is suggested that either one of the two formulae provided by Van der Merwe and Mathey (2013c) are used to design squat coal pillars:
Strength = 6.61 w0.5/h0.7 MPa (maximum likelihood method - MLM) [8]
Strength = 5.47 w°.8/h MPa (overlap reduction technique - OR) [9]
It will be noted from Figure 7 that Equations [8] and [9] predict a markedly different strength for squat pillars. According to Equation [9], a 3 m high pillar is predicted to have 50 % higher strength at w/h = 6 and 75 % higher strength at w/h = 10 as compared to Equation [8]. Therefore, designing bord-and-pillar layouts based on Equation [9] will result in improved extraction of coal, which even exceeds the economic advantages of the South African squat coal pillar formula. However, it should be noted that even with Equation [9] the extraction rates of a bord-and-pillar panel at depth exceeding 300 m would remain less than 40%. This may render the bord-and-pillar method uneconomic for coal mining at greater depth
> From a safety point of view, no experience is available to date that may argue against the use of any of these two formulae. The positive performance of squat pillars in the South African database of stable cases can be explained by both Equations [8] and [9]. Both formulae also perform equally well when tested against the database of failed slender pillars (w/h < 5) in South Africa (i.e. both formulae predict an average safety factor of failed cases close to SF = 1 with an appreciably small standard deviation). However, Equation [9] has the additional advantage that it distinguishes between failed and stable cases with improved reliability
> An additional argument in favour of Equation [9] is that it predicts a very similar rate of strength increase as Equation [5], which was developed by Bieniawski from the three large-scale in situ compression tests in South Africa. Figure 7 provides a plot of Equation [5] for a seam strength value of σc= 6.4 MPa (Pittsburgh coal), which Bieniawski found suitable for pillar design up to w/h = 12.

It is strongly recommended that any squat pillar design based on Equation [9] should be accompanied by an appropriate pillar monitoring programme.
References
Barron, K. and Pen, Y. 1992. A revised model for coal pillar strength. Proceedings of the Workshop on Coal Pillar Mechanics and Design, Pittsburgh. US Department of the Interior, Bureau of Mines. pp. 144-157. [ Links ]
Bieniawski, Z.T. 1968a. In situ strength and deformation characteristics of coal. Engineering Geology, vol. 2, no. 5. pp. 325-340. [ Links ]
Bieniawski, Z.T. 1968b. The compressive strength of hard rock. Tydskrif vir Natuurwetenskappe, vol. 8. pp. 163-182. [ Links ]
Bieniawski, Z.T. 1992. A method revisited: coal pillar strength formula based on field investigations. Proceedings of the Workshop on Coal Pillar Mechanics and Design, Pittsburgh. US Department of the Interior, Bureau of Mines. pp. 158-165. [ Links ]
Bieniawski, Z.T. and Van Heerden, W.L. 1975. The significance of in situ tests on large rock specimens. International Journal of Rock Mechanics and Mining Sciences and Geomechanics Abstracts, vol. 12. pp. 101-113. [ Links ]
Cruise, J.A. 1969. The determination of the strength characteristics of wide pillars. Master's thesis, University of the Witwatersrand. [ Links ]
DAS, M.N. 1986. Influence of width/height ratio on post-failure behaviour of coal. International Journal of Mining and Geological Engineering, vol. 4, no. 1. pp. 79-87. [ Links ]
Esterhuizen, E., Mark, C., and Murphy, M.M. 2010a. Numerical model calibration for simulating coal pillars, gob and overburden response. Proceeding of the 29th International Conference on Ground Control in Mining, Morgantown, WV. pp. 46-57. [ Links ]
Esterhuizen, E., Mark, C. and Murphy, M.M. 2010b. The ground response curve, pillar loading and pillar failure in coal mines. Proceeding of the 29th International Conference on Ground Control in Mining, Morgantown, WV. pp. 19-27. [ Links ]
Esterhuizen, G.S. 2010. Jointing effects on pillar strength. Proceeding of the 19th International Conference on Ground Control in Mining, Morgantown, WV. pp. 285-290. [ Links ]
Galvin, J.M. and Hebblewhite, B.K 1995. UNSW pillar design methodology. Research Release, vol. 1. University of New South Wales. [ Links ]
Galvin, J.M., Hebblewhite, B K., and Salamon, M.D.G. 1999. University of New South Wales coal pillar strength determinations for Australian and South African mining conditions, Proceedings of the Second International Workshop on Coal Pillar Mechanics and Design. National Institute for Occupational Safety and Health, Report IC. pp. 63-71. [ Links ]
Holland, C.T. 1942. Physical properties of coal and associated rock as related to the causes of bumps in coal mines. Technical publication no. 1406. American Institute of Mining and Metallurgical Engineers. pp. 1-17. [ Links ]
Khair, A.W. 1994. Integrated coal pillar strength formula. Preprints, vol. 155. Society of Mining Engineers of AIME. [ Links ]
Kroeger, E.B., Roethe, E., and Lí, X. 2004. Laboratory strength testing of coal from selected Illinois Seams. Proceedings of the 23rd International Conference on Ground Control in Mining, Morgantown, WV. Department of Mining Engineering, College of Mineral and Energy Resources, West Virginia University, pp. 77-85. [ Links ]
Lu, J., Ray, A., Morsy, K.. and Peng, S. 2008. Effects of rock/coal interface property in coal pillar strength. Proceedings of the 27th International Conference on Ground Control in Mining, Morgantown, WV. pp. 262-267. [ Links ]
Madden, B.J. 1990. An investigation into the factors affecting the strength of pillars in South African coal mines. PhD thesis, University of the Witwatersrand. [ Links ]
Madden, B.J. 1991. A re-assessment of coal-pillar design. Journal of the South African Institute of Mining and Metallurgy, vol. 91, no. 1. pp. 27-37. [ Links ]
Madden, B.J. and Canbulat, I. 1995. A re-assessment of coal pillar design procedures. Final project report, SIMRAC project no. COL 021. Safety in Mines Research Advisory Committee, Johannesburg. [ Links ]
Maleki, H. 1992. In situ pillar strength and failure mechanisms for US coal seams. Proceedings of the Workshop on Coal Pillar Mechanics and Design, Pittsburgh. US Department of the Interior, Bureau of Mines. pp. 73-77. [ Links ]
Mark, C. 2000. State-of-the-art in coal pillar design. Transactions of the Society for Mining, Metallurgy and Exploration Inc., vol. 308. pp. 123-128. [ Links ]
Meikle, P. and Holland, C. T. 1965. The effect of friction on the strength of model coal pillars. Transactions of the Society for Mining, Metallurgy and Exploration Inc., vol. 232, no. 2. pp. 322-327. [ Links ]
Napier, J.A.L. and Malan, D.F. 2007. The computational analysis of shallow depth tabular mining problems. Journal of the Southern African Institute of Mining and Metallurgy, vol. 107, no. 11. pp. 725-742. [ Links ]
Salamon, M.D.G. 1992. Strength and stability of coal pillars. Proceedings of the Workshop on Coal Pillar Mechanics and Design, Pittsburgh. US Department of the Interior, Bureau of Mines. pp. 94-121. [ Links ]
Salamon, M.D.G., Badr, S., Mendoza, R. and Ozbay, M.U. 2003. Pillar failure in deep coal seams: numerical simulation. Proceedings of the 10th ISRM Congress, Sandton, South Africa. pp. 1011-1018. [ Links ]
Salamon, M.D.G., Canbulat, I. and Ryder, J.A. 2006. Development of seam-specific strength formulae for South African collieries. Final research report, Coaltech 2020, Task 2.16. [ Links ]
Salamon, M.D.G., Galvin, J.M., Hocking, G., and Anderson, I. 1996. Coal pillar strength from back calculation. Research Report 1/96, School of Mining Engineering, University of New South Wales. [ Links ]
Salamon, M.D.G. and Munro, A.H. 1967. A study of strength of coal pillars. Journal of the South African Institute of Mining and Metallurgy, vol. 68, no. 2. pp. 55-67. [ Links ]
Salamon, M.D.G. and Oravecz, K.I. 1973. Rock mechanics in coal mining. Research report no. 26/73. Chamber of Mines Research Organization, Johannesburg. [ Links ]
Salamon, M.D.G. and Wagner, H. 1985. Practical experiences in the design of coal pillars. Proceedings of the 21st International Conference of Safety in Mines Research Institutes, Sydney, Australia. pp. 3-9. [ Links ]
Shen, B., Alehossein, H., Poulsen, B., Huddlestone-Jolmes, C., and Zhou, B. 2010. Collingwood Park mine remediation - subsidence control using fly ash backfilling. Report EP 105068, CSIRO Earth Science and Resource Engineering. [ Links ]
Sheorey, P.R. 1992. Pillar strength considering in situ stresses. Proceedings of the Workshop on Coal Pillar Mechanics and Design. Pittsburgh. US Department of the Interior, Bureau of Mines. pp. 122-127. [ Links ]
Sheorey, P.R., Das, M.N., BaratT, D., Prasad, R.K., and Singh, B. 1987. Coal pillar strength estimation from failed and stable cases. International Journal of Rock Mechanics and Mining Sciences and Geomechanics Abstracts, vol. 24, no. 6. pp. 347-355. [ Links ]
Su, D.W.H. and Hasenfus, G.J. 1999. Coal pillar strength and practical coal pillar design considerations. Proceedings of the Second International Workshop on Coal Pillar Mechanics and Design. National Institute for Occupational Safety and Health. pp. 155-162. [ Links ]
Tesarik, D.R., Whyatt, J.K., and Larson, M.K. 2013. Inferring mine floor properties from pillar size and floor heave. Proceedings of the 47th US Rock Mechanics/Geomechanics Symposium. American Rock Mechanics Association. [ Links ]
Wagner, H. 1974. Determination of the complete load-deformation characteristics of coal pillars. Proceedings of the 3rd ISRM Congress, Denver, CO. US National Academy of Sciences. pp. 1076-1081. [ Links ]
Wilson, A.H. 1981. Stress and stability in coal ribsides and pillars. Proceedings of the First International Conference on Ground Control in Mining, Morgantown, WV. West Virginia University. pp. 1-12. [ Links ]
Van Heerden, W.L. 1975. In situ complete stress-strain characteristics of large coal specimens. Journal of the South African Institute of Mining and Metallurgy, vol. 75. pp. 207-217. [ Links ]
Van Der Merwe, J.N. 2003. New pillar strength formula for South African coal. Journal of the South African Institute of Mining and Metallurgy, vol. 103, no. 5. pp. 281-292. [ Links ]
Van Der Merwe, J.N. and Mathey, M. 2013a. Probability of failure of South African coal pillars. Journal of the Southern African Institute of Mining and Metallurgy, vol. 113, no. 11. pp. 849-857. [ Links ]
Van Der Merwe, J.N. and Mathey, M. 2013b. Update of coal pillar database for South African coal mining. Journal of the Southern African Institute of Mining and Metallurgy, vol. 113, no. 11. pp. 825-840. [ Links ]
Van Der Merwe, J.N. and Mathey, M. 2013c. Update of coal pillar strength formulae for South African coal using two methods of analysis. Journal of the Southern African Institute of Mining and Metallurgy, vol. 113, no. 11. pp. 841-847. [ Links ]
York, G., Canbulat, I., Kabeya, K K., Le Bron, K., Watson, B P., and Williams, S.B. 1998. Develop guidelines for the design of pillar systems for shallow and intermediate depth, tabular, hard rock mines and provide a methodology for assessing hangingwall stability and support requirements for the panels between pillars. Final project report, SIMRAC project no. GAP 334. Safety in Mines Research Advisory Committee, Johannesburg. [ Links ]
Paper received Sep. 2015
Revised paper received Nov. 2015.














