PAPERS OF GENERAL INTEREST

 

The development of a time-based probabilistic sinkhole prediction method for coal mining in the Witbank and Highveld coalfields

 

 

J.N. van der Merwe

Visiting Professor, School of Mining Engineering, University of the Witwatersrand

Correspondence

 

 

---

SYNOPSIS

There is a growing need for a method to predict sinkhole occurrence. The paper describes the development of a method to predict the occurrence of sinkholes due to mining, caused by the progressive collapse of underground openings. The shape of the collapse cavity is assumed to be conical. If the top of the cavity reaches or extends beyond the base of weathering, sinkhole development is likely. Progression of the collapse may be terminated by wedging out of the cavity, choking by bulking of the collapsed material, or the presence of a strong layer between the mining horizon and the base of the weathered material. The likelihood of failure of the strong layers is evaluated as a probability of failure based on the frequency distribution of tensile strength derived from more than 800 tests on sandstone samples from the industry. Time is brought into the equation by including the rate at which bord widths increase. As the bords increase, the probability of failure of the strong layers increases. The end result is a method on which to base the probability of sinkhole occurrence with respect to time.

Keywords: sinkhole, collapse cavity, time, bulking, wedging, probability of failure.

---

 

 

Introduction

There is growing concern worldwide about the unexpected appearance of vertical-sided sinkholes, even to the extent where more than one reality television series has recently been devoted to the topic. Well-known examples include the cities of Paris and Rome, certain areas of Wales and England, and the USA.

Sinkholes may be caused by a number of factors, one of which is mining. This paper is concerned with mining-related sinkholes. Mining may result in two main types of surface disturbance, the first of which is shallow trough-shaped subsidence caused by high-extraction mining (in which case the overburden rock is allowed to collapse) or collapse of the support pillars. The second is vertical-sided, deeper sinkholes that may have catastrophic consequences.

The latter phenomenon is the subject of this paper. These sinkholes are caused by progressive collapse of the roof rocks, which may in some cases migrate to the surface, resulting in a sinkhole. It is known that the sinkholes seldom appear at the time of mining. There is a delay that can span several decades or even several centuries, such as the sinkholes in Rome and Paris that are caused by mining two thousand years ago.

The typical profile of a sinkhole-prone area is one where underground mining was by bord and pillar methods and where the mining was shallow, typically less than 30 m below surface.

Worldwide, there are very few examples of sinkholes appearing where mining was deeper than 30 m. In several countries it has become a norm to apply a safety sinkhole-prone of 2 and then to regard areas where mining was less than 60 m deep, as sinkhole-prones. The approach in typical surface disturbance risk assessments is to regard areas where mining was deeper that 60 m as safe from sinkhole risk, and then either declare shallower mining areas as definite risk areas or embark on more detailed investigations.

Over the years, methods to evaluate mining-related sinkhole risk have been developed, but the existing models have two important shortcomings: they result in an evaluation that is either positive or negative without addressing the probability of occurrence of sinkholes, and they do not address the issue of time.

This paper describes the development of a method that attempts to overcome these two shortcomings.

 

Previous models

Over the years, a number of sinkhole prediction methods have been developed. In this section a number of representative basic methods are briefly discussed. This is by no means a comprehensive discussion of previous work - rather, the papers selected are considered to be representative of certain approaches to the problem.

Depth as a norm

This very basic method is based on observations worldwide that sinkholes very rarely develop in areas where the depth of the mining horizon exceeds 30 m. To be safe, that depth was doubled to 60 m, and areas where the minimum mining depth was greater than that were considered to be stable and the rest as sinkhole-prone. Another interpretation is that where the mining depth was less than 60 m, further investigation is required, while for the deeper areas no risk is foreseen. This very basic approach does not consider the mechanism of sinkhole development beyond that it is the end result of progressive roof collapse.

Singh (2000) described sinkholes in a number of countries and developed an equation that related the maximum mining depth at which sinkholes can appear to the ratio of overburden depth to mining height. However, the data included sinkholes caused by soil erosion along fault planes (i.e. not directly related to underground overburden collapse) and the equation does not take the depth of weathering into account.

Canbulat et al. (2017) reported that in Australia the majority of sinkholes appeared at mining depths from 10 to 15 m, the average depth being 15.9 m. Only 23 of the recorded cases (10% of the total) occurred for depths greater than 30 m.

There appears to be general consensus that sinkhole occurrence is limited to shallow mining depths, generally less than 60 m.

Stability graph method

This method, initially developed for caving mining, is described in Potvin, Hudyma, and Miller (1988). It has also been used for sinkhole prediction as the mechanism of roof collapse is common to both. The method essentially rests on the size of the opening underground, which is then compared to the critical size for rock quality. The size of the opening is standardized as the hydraulic radius, which is the circular equivalent of any shape of opening. The rock quality is determined by a modified Rock Mass Rating and the critical size is determined empirically by considering a large number of case histories where collapse did or did not occur.

The method therefore takes cognisance of the size of the opening as well as rock quality (while not directly allowing for layers of different rock quality), but does not address time or the probability of failure. It also stops at the point where the immediate roof does or does not collapse and it does not explicitly address the progression of the collapse.

Methods based on the mechanism of failure and progression of collapse

Canbulat et al. (2002) described a method to predict the maximum height of roof collapse based on the bulking factor of the collapsed material, the mining height, and bord width. They used a cylindrical model for the collapse cavity. Their method included the possible arresting capability of strong layers in the overlying rock mass, but it was based on the behaviour of a clamped beam as opposed to a plate. As with the other methods described here, there was no consideration of time or the probability of occurrence.

Time of collapse

Dyne (1998) analysed the incubation time of sinkholes treated in a three-year period in Pennsylvania, USA. Based on that data, Figure 1 shows that the most frequent incubation time for the study area was 60 years. Although no attempt was made to develop a method to predict the time of occurrence, the data illustrates that there is a time delay between mining and sinkhole appearance.

 

 

Probabilistic approach

Canbulat et al. (2017) describe a stochastic method to determine the likelihood of sinkhole occurrence. However, the method does not take the arresting possibility of strong layers in the overburden or time into account, and is fundamentally based on the bulking mode of termination only for a cylindrical shape of the roof collapse.

 

Proposed methodology

The fundamental methodology that is proposed in this paper is to base the collapse model on a conical shape, and if the height of the collapse cavity reaches or exceeds the weathered rock material, a sinkhole is considered possible. The possible arresting of sinkhole development by strong layers in the overburden is then considered and the probability of collapse is determined based on the distribution of tensile strength of the strong layers. Finally, time is taken into account by incorporating the time-related increase in bord width due to pillar sidewall scaling. The end result is then the determination of the probability of sinkhole occurrence as a function of time.

The progression of the collapse cavity is then terminated by one of two possible mechanisms, namely wedging out due to the conical shape or choking of the cavity due to bulking of the collapsed material.

Figure 2 shows six possible outcomes. Note that the weathered zone is supplemented by a 'safety net', based on the level of confidence in the geological data. The less the confidence, the greater the safety net that should be applied. In the diagram, cases 1 to 3 relate to the wedging mechanism of termination and cases 4 to 6 to the bulking mechanism if it occurs prior to wedging out.

 

 

The first step in the process is to determine the maximum height of the collapse cavity, using the equations supplied in van der Merwe (2018). They are repeated here for convenience. The concept and terminology are explained in Figure 3.

 

 

For the bulking mechanism,

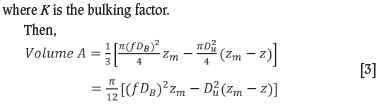
where

f = ratio of bottom of sinkhole diameter to bord width (i.e. for sinkhole diameter equal to intersection width,f = 1.414)

D_B= bord width z = height of choked volume

zm = maximum height of cavity when it wedges out

D_u= diameter of top of choked cavity

Φ = caving angle, measured off the vertical

where h = mining height

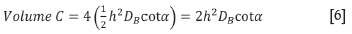
where α = angle of repose of collapsed material measured from the horizontal.

Substitution of Equations [3] to [6] into [2] results in a cubical expression for z, which is easiest found by iteration.

Also,

The maximum height of the cavity is then the smallest value of z obtained with Equations [2] to [6] - termination by choking, or z_mobtained with Equation [7] - termination by wedging out.

If the outcome of this first step results in either case 1 or case

6 shown in Figure 3, sinkhole development is considered unlikely and further investigation is not required. However, in all other cases there is the possibility that the cavity may be terminated by the presence of a strong layer in the overburden, and further investigation is required.

 

Failure mode of strong layer

A strong layer in the overburden can conceptually fail in either tension or shear. For shear failure to occur, the shear stress around the edges of a circular disc must be greater than the shear strength.

The shear stress is given by

In practical terms this means that for a plate of diameter 20 m and loaded by the dead weight of 60 m of overburden rock (i.e. beyond the extremes of common coal mining configurations), the shear stress will be 7.5 MPa. This is less than commonly quoted values of shear strength of 15 MPa given by van der Merwe and Madden (2010) or 35 MPa according to Geertsema (2000). The shear mode of failure can thus be ignored for this investigation.

For the tensile failure mechanism, the strong layer is assumed to behave similar to a clamped plate, not a beam as previously used. The beam analogy is valid for a rectangular opening with length much greater than width. The top of a collapse area has been seen to be circular or elliptical in shape and therefore the plate analogy is more acceptable. The tensile stress developed around the edges of a uniformly loaded clamped circular plate is given by

where

γ = uniformly distributed load

D = diameter of plate

t = thickness of plate

If the tensile strength of the material is denoted by a_m, the tensile safety factor is

From a deterministic perspective, failure will occur if S_Pt < 1.

 

Identification of strong layer

The next step is to determine which of the overburden layers can be considered as 'strong'. Typical coal mining overburden in the Witbank coalfield consists of sedimentary rock types, mainly sandstone, shale, mudstone, siltstone, and laminated shale/ sandstone layers.

The results of a great number of tensile strength tests based on the Brazilian test method (UTB) were collected from rock engineers in the Witbank coalfield. The results were loosely grouped as sandstone, shale, coal, and laminated material. It was found that the frequency distributions could be described as lognormal. The results are summarized in Table I.

 

 

The cumulative frequency distributions are shown in Figure 4.

 

 

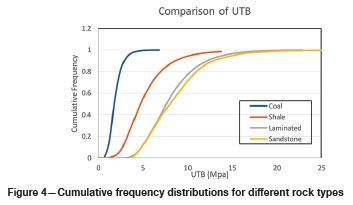
It is clear from Table I and Figure 4 that there are distinct differences between the tensile strengths of the different rock types, and that the sandstone and laminated rock are significantb stronger than the others. The sandstone only can then be regarded as the strong layer. The laminated layers should not be included due to the rapid weathering of the shale laminations.

It was found that the cumulative distribution of the tensile strength of sandstone can be expressed by the simplified equation:

where o_t is the tensile strength in MPa.

 

Probability of failure

Equation [11] also expresses the probability of failure of the strong layer. Therefore, instead of calculating a safety factor for the strong layer, the tensile stress can now be used to determine the probability of failure.

The equation for the tensile stress is given by Equation [9].

For clarity, the elements of Equation [9] are given by the following equations. The terminology is explained in Figure 5.

 

 

 

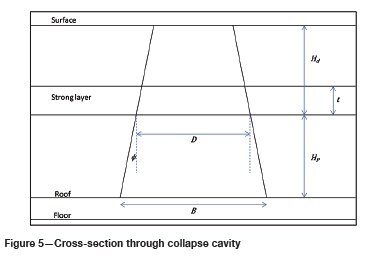
where H_dis the depth below surface of the base of the strong layer.

where

B = diameter of the bottom of the collapse cavity (typically taken as the intersection width) Φ = caving angle measured off the vertical HP = parting thickness between the roof of the excavation and the bottom of the strong layer.

 

Probability of sinkhole occurrence

There will invariably be more than one strong layer. A sinkhole can appear only if all the strong layers fail. Therefore, the probability of failure of the system, P_S, is the product of all the individual probabilities of failure. Mathematically,

where P₁ to P_n are the probabilities of failure of each of the individual strong layers.

Note that this procedure is dominated by the strongest of the strong layers. A layer with a very high probability of failure (i.e. close to 1.0) will not change the outcome, while layers with very low probabilities of failure (close to zero) will have a meaningful impact. If there is only a single layer that does not fail, the system will not fail either and no sinkhole will occur.

This is a simplified approach, as even the weakest of layers will contribute to some extent to stability. This is not taken into account in this proposed procedure as it has been shown that the tensile strength of the sandstone is dominant, and a conservative approach was followed in the investigation. The weaker rock types are also more susceptible to rapid weathering.

The approach can easily be extended to the other rock types by substituting Equation [11] with an equation which is appropriate for that particular rock type. The rest of the procedure will not require modification.

 

Extension of the procedure to include time

There are at least two mechanisms that will weaken the system over time. One is weathering of the rock, which will decrease the tensile strength, and the second is widening of the base of the collapse cavity, which will increase the tensile stress of the overlying layers.

Judging from observation of exposed borehole core, rock types like shale or mudstone weather fairly quickly, but sandstone weathering is a much slower process. Weathering also affects one layer at a time - only the exposed layer at the top of the collapse cavity.

Widening of the bord width by sidewall scaling is a much faster process and it affects all the overlying layers at the same time. It is therefore regarded as the dominant mechanism by which the probability of failure will increase over time.

The rate at which the sidewalls scale has been quantified, and by implication the rate at which the probability of failure increases over time can also be quantified. According to van der Merwe (2016) the amount by which pillar width decreases over time, which is the same as the amount by which the bord width increases, is given by

where

h = mining height

T = time since mining

m = constant, 0.1799 for the Witbank and Highveld coal seams (excluding the No. 5 Seam)

x = constant, 0.7549 for the Witbank and Highveld coal seams (excluding the No. 5 Seam).

The probability of failure at any given point in time can now be obtained by substituting D_Bby D_B+d_T in the foregoing equations.

 

Practical considerations

The procedure outlined in the foregoing paragraphs is sensitive to all the input parameters. For a more complete discussion of the impact of variability of the input parameters, refer to van der Merwe (2018).

There are two classes of input parameters, namely the controllable and uncontrollable ones. At the planning and mining phases, the bord width is the main controllable parameter while the mining height is controllable to some extent.

The remaining parameters are not controllable. In this class, some are easier to determine than others. The lithology is relatively simple to define, although the level of detail contained in older borehole descriptions is not always adequate. The bulking factor and caving angle are more difficult to determine but not impossible. It is essential that local databases should be set up and maintained.

It was shown in Figure 4 that the laminated rock has tensile strength equivalent to that of sandstone, but due to the rapid weathering nature of the shales, should not be considered as strong layers in the context of this type of investigation. Cross-bedded sandstone should also be viewed with suspicion.

 

Application to case study

The procedure described in the paper was applied to a case study to demonstrate its applicability. The name of the mine is withheld for confidentiality.

At Mine A, two previously mined areas, Sites 1 and 2, were evaluated for the potential of sinkhole occurrence. Table II summarizes the information that was used as input for the conical collapse model at the time, without taking the effect of strong layers or time into account.

 

 

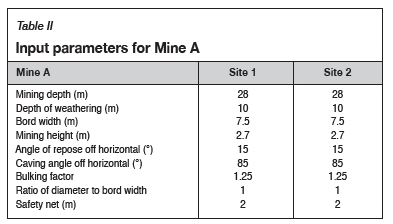
The cases are seen to be similar from a mining perspective. In both cases, the potential mode of termination was found to be bulking; the height of the cavity, 25.1 m, reached the weathered zone and the verdict was that sinkholes were likely to occur. The same mitigation methods were then applied to the two areas.

The procedure dealing with the impact of strong layers described in this paper was then applied to the two cases. The base depth and thickness of sandstone in the two areas are indicated in Table III.

 

 

Table III shows that although the base depths of the sandstones are similar, the thicknesses are different. It was then found that for Site 1, the probability of sinkhole occurrence at the time of mining was 0.5% while for Site 2 it was 25.3%. The progressions of the probabilities of occurrence over a period of 250 years are shown in Figure 6.

 

 

Figure 6 indicates that for Site 2, the probability of occurrence of 50% is reached after 39 years. At that time, the probability of occurrence for Site 1 is only approximately 8%. Taking this additional information into account, it is clear that Site 2 requires much more urgent mitigation and perhaps even a different approach than Site 1.

This case study also highlights the importance of detailed description of borehole logs.

 

Restrictions and further development

Input accuracy

The most important restrictions to the application of the procedure outlined here relate to the availability and accuracy of the input parameters. This includes the caving angle, bulking factor, the mining geometry, and the borehole log descriptions.

With increasing emphasis on the time-related impact of mining on the environment there is a growing need to evaluate older mining areas for sinkhole potential. In the older areas, where mining was done up to 100 years or more ago, the data is especially suspect. At the time of mining the emphasis on information gathering was on the thickness and depth of economical coal seams, with sparse attention paid to the detail of the overburden rock. In fact, some logs exist that contain three entries only, namely soil, rock, and coal. The mine plans can also sometimes contain inaccurate information.

In cases where sinkhole evaluation of older areas is required now, there are no short cuts to determine more suitable input information and new drilling is required. Where this is to be done, it is strongly advocated that the visual descriptions be supplemented with wireline logging and geotechnical evaluation. The lessons from the past should be heeded and as much information as possible should be gathered when the opportunity arises.

Rate and extent of pillar scaling

The method is also sensitive to the rate and extent of pillar scaling. This should be re-evaluated at suitable times. It is not only applied to the temporal development of sinkhole occurrence, but is also used for the prediction of the time of failure of coal pillars.

It is also logical that the presence of roof collapse debris in the cavity will restrict the pillar scaling, and vice versa. In this paper, quantification of that impact is not attempted. However, it should be borne in mind that for pillar scaling to take place, it is not necessary for the fractured pillar material to be completely detached from the pillars. There just needs to be a fracture.

On the other side of the equation, the bulked and collapsed material will undergo slight compression due to the weight of the overlying collapsed material and this will reduce the bulking factor. This mechanism counteracts the omission of the effect of bulking of the pillar debris, at least to some extent.

The presence of debris can only slow the process down, not terminate it, and therefore not taking it into account at this stage results in a conservative view. This is an area that should be identified for further development of the methodology described here.

Multiple seam mining

The process outlined here is based on the consideration of mining on a single seam only. In the case of multiple seam mining the bottom seam should be analysed first. If it is found that the cavity on the bottom seam does not reach the upper seam, the next highest seam should be analysed as an independent entity. The process should be repeated for the other overlying seams in sequence.

If the cavity on a lower lying seam does reach a higher seam, two scenarios should be investigated. If the mining layouts are not superimposed, the potential for the bottom seam cavity to result in pillar failure of the upper seam should be considered.

If the layouts were superimposed the cavity from the bottom seam will reach an intersection or bord on the upper seam. The upper seam should then be analysed with an adapted Equation [3]. A volume equal to the remaining open void from the bottom seam, V_L, should be added to the volume available for cavity growth on the upper seam.

In mathematical terms, Equation [3] should then be:

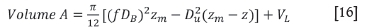
Note that as the bottom seam cavity does not impact on the bord width, the equations for evaluating the stability of strong layers will not be affected.

Further development of the model

This model only recognizes the variability of a single input parameter, namely the tensile strength of sandstone layers. Canbulat et al. (2017) showed the benefit of a full stochastic approach to the problem, even though the impact of strong layers and the effects of time were not included in their work. The two approaches should be combined.

The resisting effects of the weaker layers should also be incorporated, as should the rate of chemical weathering of the overburden rock types. These two parameters are to some extent mutually compensating, as weathering will reduce the strength and thereby increase the probability of failure, while taking the effect of weak layers into account will reduce the probability of failure.

The extensions will no doubt result in a much more complex model, but certainly not one beyond the reach of commonly available methods of calculation.

 

Conclusions

The process described in the paper is a further development of the existing models to evaluate the potential for sinkhole occurrence due to shallow mining. The first model that was used was based on the concept of the termination of cavity development by choking of a cylindrical cavity due to bulking of the collapsed roof material. This was subsequently extended to a cavity of conical shape and a second mechanism of termination was introduced, namely wedging out of the cavity.

This model extends the conical model by recognizing the potentially stabilizing effect of strong layers in the overburden on a probabilistic basis. By incorporating the temporal widening of the bord width due to pillar scaling, the probability of sinkhole occurrence is linked to time.

It was shown by the application of the method to a case study that the procedure results in more useful information to evaluate the potential for sinkhole occurrence.

In principle the method in itself is not restricted to coal mining, but the constants that were used for some of the variables restrict the detailed method of calculation to the Witbank and Highveld coalfields with the exception of the No. 5 Seam. By substituting the constants by appropriate ones for other coalfields and even other bord and pillar mining like chrome or platinum, the application of the model can be extended.

The model should be developed further by incorporating the variability of all the input parameters. This will require more data to be gathered and the accuracy of data to be improved.

 

Acknowledgements

Mr Dave Neal is thanked for his persistent encouragement to develop the model and for gathering the data of UTB tests from all available sources in the industry.

Rock engineers from the mines in the Witbank and Highveld coalfields are acknowledged for sharing the data.

Ms Jeanne Walls reviewed the paper prior to submission.

The paper is published with the permission of South32.

ORCiD ID:

J.N. van der Merwe: https://orchid.org/0000-0002-3709-5520

 

References

Canbulat, I., Zhang, C., Black, K., J Johnston, J., and McDonald, S. 2017. Assessment of sinkhole risk in shallow coal mining. Proceedings of the Tenth Triennial Conference on Coal Mine Subsidence: Adaptive Innovationfor Managing Challenges, Kirkton Park, Pokolbin, 5-7 November 2017. Mine Subsidence Technological Society, Institution of Engineers Australia, Canberra.         [ Links ]

Canbulat, I., van der Merwe, J.N., van Zyl, M., Wilkinson, A., Daehnke, A., and Ryder, J. 2002. Task 6.9.1: The development of techniques to predict and manage the impact of surface subsidence. Coaltech, Johannesburg.         [ Links ]

Dyne, LA. 1998. The prediction and occurrence of chimney subsidence in southwestern Pennsylvania. MSc thesis, Virginia Polytechnic Institute and State University, Blacksburg, VA.         [ Links ]

Geertsema, A.J. 2000. The engineering characteristics of important southern African rock types with emphasis on shear strength of concrete dam foundations. WRC Report No 433/1/00: Water Research Commission, Department of Water Affairs, Pretoria.         [ Links ]

Potvin, Y., Hudyma, M., and Miller, H.D.S. 1988. The stability graph method for open stope design. Proceedings of the 90th Canadian Institute of Mining AGM, May 1988. CIM, Montreal. Paper no. 44.         [ Links ]

Singh, K.B. 2000. Causes and remedial actions of pot-hole subsidence due to coal ining. Journal of Scientific & Industrial Research, India, vol. 59, April. p. 280-285.         [ Links ]

Van der Merwe, J.N. 2016. A three-tier method of stability evaluation for coal mines. Journal of the Southern African Institute of Mining and Metallurgy, vol.116, no. 12. http://dx.doi.org/10.17159/2411-9717/2016/v116n12a14        [ Links ]

Van der Merwe, J.N. 2018. Effects of coal mining on surface topography in South Africa - updates and extensions. Journal of the Southern African Institute of Mining and Metallurgy, vol. 118, no. 7. http://dx.doi.org/10.17159/2411-9717/2018/v118n7a11        [ Links ]

 

 

Correspondence:
J.N. van der Merwe
Email: nielen@stablestrata.com

Received: 15 May 2019
Revised: 1 May 2020
Accepted: 20 Jun. 2020
Published: June 2020