Services on Demand
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
SAIEE Africa Research Journal
On-line version ISSN 1991-1696
Print version ISSN 0038-2221
SAIEE ARJ vol.114 n.4 Observatory, Johannesburg Dec. 2023
An Image Encryption Based on Confusion-Diffusion Using Two Chaotic Maps and Frobenius Endomorphism
Asmaa HilmiI; Soufiane MezrouiII; Ahmed El OualkadiIII
IAbdelmalek Essaadi University National school of applied sciences of Tangier (ENSATg) Laboratory of Information and Communication Technologies (LabTIC) ENSA Tanger, Route Ziaten, BP 1818, Tanger principale, Morocco. E-mail: asmaa00hilmi@gmail.com
IIAbdelmalek Essaadi University National School of applied sciences of Tangier (ENSATg) Mathematics and Intelligent Systems team (MASI) ENSA Tanger, Route Ziaten,BP 1818, Tanger principale, Morocco. E-mail: mezroui.soufiane@vahoo.fr
IIIMember, IEEE. Abdelmalek Essaadi University National school of applied sciences of Tetouan (ENSATe) Laboratoire d'Ingénierie des Systèmes Innovants (ISI) ENSA Tetouan, Avenue Palestine B.P 2222, M'hannech II-Tetouan, Morocco. E-mail: eloualkadi@gmail.com
ABSTRACT
The chaotic map including 2D-Henon and Tent maps, have been widely used in modern cryptography, due to its high level of security and low cost of computation, compared to traditional algorithms. This study suggests a method for sharing images that are dependent on both confusion and diffusion for securing a gray-scale image. First, a new perturbation method of pixels based on Henon map to generate the permutation matrix for scrambling the plain image is proposed. The confused image should be encrypted, in which we combine the Frobenius endomorphism and Tent chaotic map to generate a key encryption. Using the eXclusive-OR operation, the substitution process is realized between the key encryption and confused image. The simulation results of the proposed scheme maintain a lossless encryption quality, and the security analysis, which includes differential attack, entropy, correlation coefficient, and histogram analysis illustrate that the proposed approach reveals a high performance.
Index Terms: 2D-Henon map, Chaotic cryptography, Frobenius endomorphism, Image encryption, Tent map
I. INTRODUCTION
With the advent of both public and hybrid cloud, ensuring a secure and reliable sharing of secret image information has become a challenge for security managers. In cryptography, most research papers improve the system security to comply with the current image encryption standards, which call for a lot of redundant information, a lot of data, and a significant of correlation [1]. In general, the encryption process depends on two phases: the permutation(confusion) phase, followed by the diffusion phase. The confusion phase is intended to adjust a pixel in a basic image in order to decrease the association between pixels [2], and the pixel values are changed during the diffusion phase. Such as Advanced Encryption Standard (AES), Elliptic Curve Cryptography (ECC) and Rivest-Shamir-Adleman (RSA), various encryption algorithms have been proposed to sharing a secret image [3-5]. However, these traditional encryption methods remain limited in front of the current image encryption requirements [6]. In addition, some authors have proposed to realize confusion and diffusion approaches based on other techniques such as Zaslavskii and Hilbert Space Filling Curve algorithms [7] or the principle of the Josephus and the filtering technology [8]. With the introduction of chaos theory in cryptography, the chaotic encryption systems become the best solution to enhance security level of image information. Several research studies have been proposed to combine two existing chaotic systems for confusion and diffusion [9, 10], or multiple chaotic maps [11], others are based on mixed multi chaos to propose new chaotic systems [12, 13]. Numerous hypothesized chaotic systems exist, some of which are one dimensional such as ID logistic map, and others are high-dimensional such as 3D chaotic systems [14], 4D [15] and 5D hyperchaotic system [16]. This paper provides a novel method for encrypting grayscale images that uses two signals produced by a 2D Henon chaotic system to pervert the original image. The 2D chaotic system has been chosen because the use of one-dimensional chaotic systems for encryption may be vulnerable to brute-force attack, high dimensional chaotic systems, however, it is expensive to implement and its performance assessment is complicated [17]. The image's pixel values are completely out of place in their position via a new transformation method to replace the values of plain image in their new positions. To realize the diffusion phase, we employ a Tent map to create a chaotic sequence. To improve the level of security, this sequence is applied with Frobenius Function to create the encryption key. Finally, each pixel's value in a scrambled image is replaced using the encryption key and an exclusive-OR operation. This research paper is structured as follows: The second section is about a literature review on image encryption approaches. The third section sheds light on some of the used methods: Henon map, Tent map and Frobenius method.
Section four describes the proposed approach. The simulation results and performances analysis are detailed in section five. The sixth and final sections conclude the paper.
II. RELATED WORKS
Overall, in the literature, several algorithms based on both confusion and diffusion using chaotic map have been proposed. The authors in [9]and [10] have proposed a chaotic scheme by using two kinds of chaotic systems, the first one is for confusion and the second is for diffusion. The position of images pixels is reorganized applying 2D Arnold cat map. Then, they have been encrypted the new reorganized image using a 1D logistic map-generated chaotic sequence. But in [10] the scrambled image is encrypted pixel by pixel using a preprocessed signal produced by a Lorenz chaotic system. In [12], a coupled map lattice (CML) is used for image encryption by combining a CML map with a logistic map and a tent map. The authors in [13] have combined the Henon and Chebyshev maps to create a new two-dimensional Henon-Chebyshev modulation map (2D-HCMM). Reference [18] has shown a novel technique for breaking images into blocks that uses a zigzag pattern [19], rotation, and random permutation to jumble the image blocks. Then, a chaotic logistic map provides a key sequence to disperse the scrambled image. In [11], Sura has proposed to split the secret image into four equally blocks, each block is rotated 90 degrees in the direction of rotation and then, numerous chaotic maps are used for confusion and diffusion with each block. The authors in [20] have shuffled the image with Zaslavskii and Hilbert Space Filling Curve algorithms [7], which consists of the confusion process. An encryption approach using the principle of the Josephus for confusion and the filtering technology for diffusion is given in [8]. The overview of the related study reveals that the construction of schemes is based on the use of multiple chaotic systems known of confusion and diffusion, or else to combine various chaotic systems in order to create a new system. Although, these methods have made it possible to provide the desired level of security, it is mainly due to the high redundancy and the data capacity presented by an image. To overcome the above-stated in terms of security, this research paper proposes a more effective technique for image encryption using 2D-Henon map, Tent map and Frobenius endomorphism. The primary innovations of this study are: first to propose a new approach which can disturb the image pixels in a random way, to be able to solve the issue of strongly correlated between two adjacent pixels, and second to create an encryption key by combining between Tent choatic map and Frobenius endomorphism. The proposed approach shows a high sensitivity to any change in encrypted images, in addition to the other properties such as randomness, correlation of pixels and lossless of the final output image.
III. REVIEW OF THE USED METHODS
The proposed approach in this paper is based on three methods: 2D Henon map, Tent map and Frobenius endomorphism. This section reviews the above-mentioned methods.
A.2D-Henon Map
One of the most used chaotic maps in modern cryptography is the 2D-Henon map. The map was proposed by Michel Henon which is a streamlined illustration of the Poincare section of the Lorenz model which is described in reference [21] by

Where, the chaotic system's parameters are a and b, and the chaotic map's initial values are a0 and bo. a=1.4 and b=0.3 represent the standard parameters values to be chaotic for Henon map.
B.Tent Map
The one-dimensional Tent map is a simplest chaotic system that indicates chaotic behavior which is defined in reference [22] by
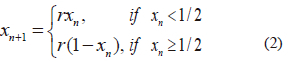
Where, r ϵ [0,2 ]
C.Frobenius Endomorphism
The Frobenius endomorphism is a special endomorphism defined in reference [23] by

Where A is a finite field and p is prime number.
A frobenius element is a power of the frobenius endomorphism for the composition low of map.
IV. THE PROPOSED APPROACH
In this section, the two principles processes, encryption and decryption, are presented. For the encryption process, the plain image is scrambled using our confused method. Then, both the Tent chaotic map and Frobenius endomorphism are used to create a key encryption to encrypt the confused image. Even so, the processes described in the encryption process are reversed in the decryption procedure. Table I shows the notations used in the rest of this paper.

A. Encryption Process
To minimize the correlation between the original image's neighboring pixels, which is in general higher, a new confusion method is presented. Fig. 1 shows the schematic for both the confusion and diffusion methods.

The specific permutation steps are organized as follows: Step (1): Let P be a plain image of M*N size.
Step (2): We generate two chaotic sequence vectors X and Y based on the 2D-Henon system, there sizes are also M and N respectively and the IX and IY are the indexes vectors of X and Y respectively.
Step (3): (X'; I'X) and (Y'; l'Y) are sorted in ascending order according to 4.
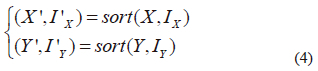
Step (4): It produces a new matrix L of size M*N. Filling out the new matrix L according to Algorithm 1 where the plain image's row and column of pixel positions are k and v, respectively. We fill the vectors h and g according to new indexes generated by X' and Y', then we fill the confused matrix L with the position of two vectors h and g.

Fig. 2 shows the detailed confusion process:

(a) and (a1): generation of two sequence vectors X and Y using 2D-Henon map, there size are M and N respectively with their indexes IX and IY.
(b) and (b'): sorting X and Y in ascending order to produce X' and Y' with their new indexes I'X and I'Y
(c) and (c'): summarized two new indexes I'X and I'Y in two vector h and g.
(d): filled the confused matrix L from the plain image P according to new position indicated in vectors h and g.
Fig. 3 shows a detailed example of the confusing approach.
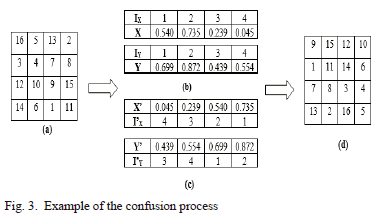
Fig. 3 (a) shows a plain image of 4*4. The two sequences chaotic vectors are generated by 2D henon map as displayed in Fig. 3 (b). However, Fig. 3 (c) shows the X' and Y' sorting from the respective X and Y vectors in ascending order. The confused matrix is shown in Fig. 3 (d) by applying the steps detailed in both Algorithm 1 and Fig. 2. The confusion method successfully disturbs the pixel values of the plain image when it is applied to some examples of images chosen for this study, as shown in Fig. 4.

The proposed method minimizes the correlation among adjacent pixels of the input image and enhances the chaos. From Fig. 1, steps 5 and describe the diffusion method used to encrypt the confused image including the key generation and diffusion process.
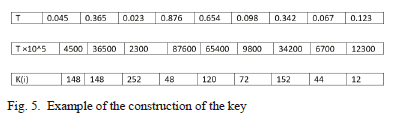
Step (5): a chaotic vector T= {Tl, T2,....T_{M*N}} is generated from the Tent Map, We apply the Frobenius function to the chaotic sequence T as follows: describe the diffusion method used to encrypt

Then, we create the key encryption using the following formula:
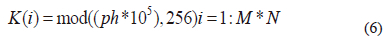
Step (6): In the diffusion process, to change the pixel value, the key K and the confused image L are combined using the eXclusive-OR (XOR) operation to produce the encrypted image C as follows:

Fig. 5 explains the key construction procedure.
B. Decryption Process
The output plain image can be recovered using the key and the encrypted image. The method of decryption can be done as follow:
1- XOR operation is used to create the dL image confusion using the K and encrypted image.

2- According to Algorithm 2, the procedure to extract the plain image from the confused image involves the steps described in the encryption process in reverse order.

V. SIMULATION RESULTS AND PERFORMANCE ANALYSIS
Table II summarizes the parameters used in the implementation of the proposed method. For the 2D Henon map and Tent map, we choose the standard values which are chaotic.
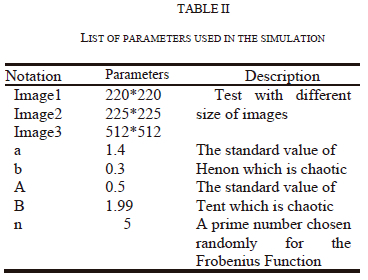
Fig. 6 shows the three plain images (Image1, Image2 and Image3), encrypted images and decrypted images respectively. According to Fig. 6, no details regarding the original image can be obtained from the encrypted images, moreover; the decrypted images restore the plain images without distortion. This section evaluates the performance of the suggested technique in terms of PSNR (Peak Signal to Noise Radio), histogram, correlation, entropy, and differential attack.

A. PSNR
The PSNR is described in [24] as the ratio of the maximum possible signal power to the maximum possible signal plus corrupted noise power. The PSNR is given by

Where, maxi represents the greatest possible pixel's value of the image, it is equal to 255. The MSE (Mean Square Error) is the average square of the error between the decrypted and plain image is known as the mean squared error. High PSNR value indicates a lower variation between the input and output image, theoretically, PSNR can be infinite if MSE is equal to 0, in this case, there is no difference among the two images, i.e., corresponding pixels of both images have similar values. When the PsNR value for the encrypted image is compared to the plain image, the PsNR is low, which results in greater encryption quality. According to Table III, the obtained encrypted images' PSNR values are really low (<9.5 dB). However, the decrypted images show infinite PsNR values which mean that they have similar values compared to the ones of the plain images. Consequently, with the proposed approach, the encrypted image cannot provide any details on the secret image and can only be used to recreate the original secret image without distortion.

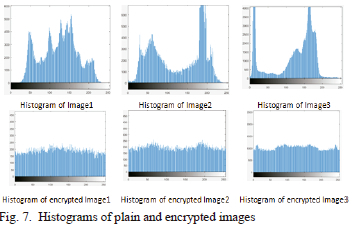
B. Histogram Analysis
The histogram presents a visual interpretation of both plain and encrypted image distribution. Fig. 7 shows the uniformly distributed histograms of the encrypted images, contrary to plain image histograms which are randomly distributed. This designates that the encryption method can be more resistant to attacks.
C. Correlation Analysis
This research aims to demonstrate how closely the plain and encrypted image are alike. Equations (10), (11), (12) and (13) can be used to express the nearby pixel's correlation coefficient factor [11]

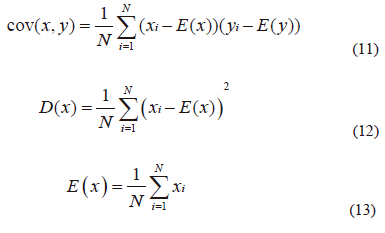
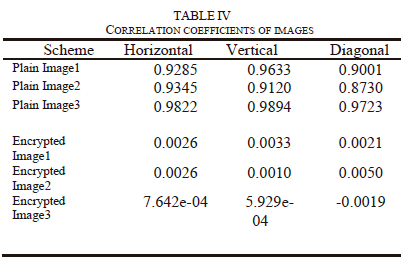
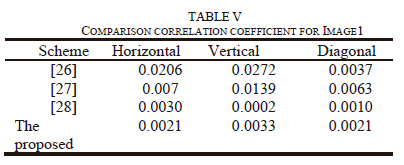
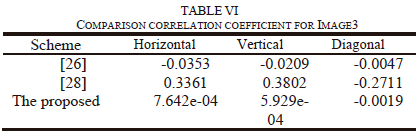
Where, in the plain or encrypted images, x and y are two adjacent pixel values, E(x) is x's average value, D(x) is the difference from the mean, cov (x, y) is the evaluation of the covariance between neighboring pixels x and y, and r{xy} is the correlation coefficient among x and y. To achieve a stronger encryption image, the correlation coefficient should be very close to zero or extremely low. Table iV shows the number obtained from correlation in original image of the horizontal, vertical, and diagonal, which are more than 0.9 which means the two neighboring pixels are strongly correlated to each other. in contrary from Table iV, in the encrypted image, the correlation coefficients for the horizontal, vertical, and diagonal directions are so close to zero. Tables V and Vi compare the results of the correlation coefficients from images 1 and 3 to those from other methods [25-28] to show that the suggested technique produces better correlation coefficient values, namely correlation coefficients that are ~ 0 in the vertical, horizontal, or diagonal directions, as required for security criteria.
D. The Randomness
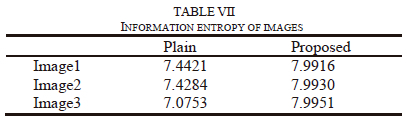
The concept of the randomness is generally measured by the Shannon entropy over the cipher image to test an image's encryption quality. it was first proposed by claude Shannon in [29] and given by

Where, X is the test random variable, xi is the ith potential value of X, and Pr (xi) is the probability that X will have the value X=xi. An ideal encrypted image is one in which the pixel values are consistently dispersed throughout. if an encrypted image is very random-like, it is thought that its entropy of information is quite similar to the theoretical maximum. Table Vii shows the entropy of encrypted images; this is very similar to 8-bit image's theoretical upper bound on entropy.
E. Analysis for Differential Attack
The encrypted image should be commonly able to detect alterations in the original image. We significantly alter the plain image to check the encryption effect's security. Then, in order to protect against differential attacks, the encryption system can nonetheless make significant updates to the encrypted image. The encryption system's security is tested using two parameters. The first is the Number of Pixels changes Rate (NPcR) and the second is the Unified Average changing intensity (UAci). Both of these variables are calculated by 15 and 16 as follows:
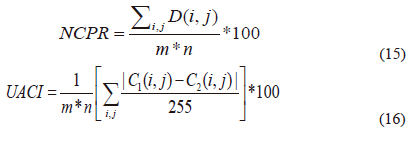
Where, Ci and C2 are two obtained encrypted images after the plain image changes. If C1((,J)^1 C2((,J) then D(ij)=1, otherwise D(i,j)=0. In Table VIII, the Image1 is compared to other approaches [25, 26, 28, 30] . This shows how closely the NCPR and UACI reflects the standard value (NCPR > 99 and UACI > 33), which designates that the proposed approach can be more resistant to the original image attack.

VI. CONCLUSION
This research paper proposes a method for image encryption based on two chaotic maps. The first chaotic map used in this approach is 2D-Henon map. The second chaotic sequences generated from 2D-Henon map are utilized to scramble the plain image according to our approach; this successfully achieves a good degree of visual confusion. In order to ensure a high level of security during the diffusion process, the Tent map is utilized to produce a chaotic sequence. This sequence is applied the Frobenius endomorphism to create key encryption. In the last one, we apply the XOR operation between the key encryption and the confused image to obtain the encrypted image. The experimental results and performance analysis based on histogram, randomness, entropy, PsNR and differential attack demonstrated that our proposed approach provided high security features. First, the suggested method can securely encrypt a variety of images. second, the proposed approach avoids the correlation between original and encrypted image, owing to the new method proposed to scramble the plain image. Moreover, the encrypted image can be decrypted without loss.
REFERENCES
[1] Y. L. T. Hu, L.H. Gong, S. F. Guo, and H. M. Yuan, "Chaotic image cryptosystem using DNA deletion and DNA insertion," Signal Processing, vol. 134, pp. 234-243, 2017, doi: 10.1016/j.sigpro.2016.12.008. [ Links ]
[2] P. Ping, J. Wu, Y. Mao, F. Xu, and J. Fan, "Design of image cipher using life like cellular automata and chaotic map," Signal Processing, pp. 233-247, 2018, doi: 10.1016/j.sigpro.2018.04.018.
[3] K. Shankar and P. Eswaran, "Sharing a Secret Image with Encapsulated Shares in Visual Cryptography," Procedia Computer Science, vol. 70, pp. 462-468, 2015, doi: 10.1016/j.procs.2015.10.080. [ Links ]
[4] K. Shankar and P. Eswaran, "RGB-Based multiple Share Creation in Visual Cryptography with Aid of Elliptic Curve Cryptography," China Communications, vol. 14, pp. 118-130, 2017, doi: 10.1109/cc.2017.7868160 [ Links ]
[5] K. Shankar and P. Eswaran, "RGB-Based Secure Share Creation in Visual Cryptography Using Optimal Elliptic Curve Cryptography Technique," Journal of Circuits, Systems, and Computers, vol. 25, pp. 1-23, 2016, doi: 10.1142/s0218126616501383. [ Links ]
[6] X. Wang and Y. Li, "Chaotic image encryption algorithm based on hybrid multi-objective particle swarm optimization and DNA sequence," Optics and Lasers in Engineering, 2020, doi: 10.1016/j.optlaseng.2020.10639.
[7] S. J. Lin, J. C. Lin, and W. P. Fang, "Visual Cryptography (VC) with Non expanded Shadow Images: Hilbert-curve Approach," presented at the IEEE International Conference on Intelligence and Security Informatics, Taiwan, 2008.
[8] Z. Hua, B. Xu, F. Jin, and H. Huang, "Image Encryption Using Josephus Problem and Filtering Diffusion," IEEE ACCESS, 2019, doi: 10.1109/access.2018.2890116.
[9] S. Sam and A. Kotal, "Confusion and Diffusion of Grayscale Images Using Multiple Chaotic Maps," presented at the National Conference on Computing and Communication Systems (NCCCS), 2012.
[10] Z. Zhang and T. Cao, "A Chaos-Based Image Encryption Scheme with Confusion- Diffusion Architecture," Springer-Verlag Berlin Heidelberg, 2011, doi: 10.1007/978-3-642-21402-8 42.
[11] S. F. Yousif, "Grayscale Image Confusion and Diffusion Based on Multiple Chaotic Maps," presented at the 1st International Scientific Conference of Engineering Sciences - 3rd Scientific Conference of Engineering Science (ISCES), 2018.
[12] Y. Liu, Z. Qin, X. Liao, and J. Wu, "A Chaotic Image Encryption Scheme Based on Henon Chebyshev Modulation Map and Genetic Operations," International Journal of Bifurcation and Chaos, 2020.
[13] X.Wang, N. Guan, H. Zhao, S. Wang, and Y. Zhang, "A new image encryption scheme based on coupling map lattices with mixed multi-chaos," Scientific Reports, 2020, doi: 10.103 8/s41598-020-66486-9.
[14] A. B. Joshi, D. Kumar, and D. C Mishra, "Security of Digital Images Based on 3D Arnold Cat Map and Elliptic Curve," International Journal of Image and Graphics, World Scientific Publishing Company, 2020, doi: 10.1142/s0219467821500066.
[15] G. Qi and G. Chen, "Analysis and circuit implementation of a new 4D chaotic system," Phys. Lett, vol. 352, pp. 386-397, 2006, doi: 10.1016/j.physleta.2005.12.03. [ Links ]
[16] Q. Yang and M. Bai, "A new 5D hyperchaotic system based on modified generalized Lorenz system," Nonlin. Dyn, vol. 88, pp. 189-221, 2017, doi: 10.1007/s11071-016-3238-7. [ Links ]
[17] W. Xingyuan, Z. Junjian, and C. Guanghui, "An image encryption algorithm based on ZigZag transform and LL compound chaotic system," Optics and Laser Technology, 2019, doi: 10.1016/j.optlastec.2019.105581.
[18] S. T. Kamal, K. M. Hosny, T. M. Elgindy, M. M. Darwish, and M. M. Fouda, "A New Image Encryption Algorithm for Grey and Color Medical Images," IEEE ACCESS, 2021, doi: 10.1109/access.2021.3063237.
[19] S. Hedge and B. Rao, "Visual Cryptography (VC) using Zigzag Scan Approach," Journal of computer science engineering and technology, vol. 1, pp. 456-461, 2011. [ Links ]
[20] P. Praveenkumar, R. Amirtharajan, K. Thenmozhi, J. Bosco, and B. Rayappan, "Fusion of confusion and diffusion: a novel image encryption approach," Telecommun Syst, vol. 65(1), pp. 69-77, 2016, doi: 10.1007/s11235-016-0212-0. [ Links ]
[21] M. Henon, "A two-dimensional mapping with a strange attractor," Communications in Mathematical Physics, vol. 50(1), pp. 69-77, 1976, doi: 10.1007/bf01608556. [ Links ]
[22] P. H. Borcherds and G. P. Mccauley, "The Digital Tent Map and the Trapezoidal Map," Chaos, Solrrons and Fracrals vol. 3, pp. 451-466, 1993. [ Links ]
[23] A. Warusfel, "Structures algébriques finies," 1971.
[24] A. T. Nasrabadi, M. A. Shirsavar, A. Ebrahimi, and M. Ghanbari, "Investigating the PSNR calculation methods for video sequences with source and channel distortions," IEEE International Symposium on Broadband Multimedia Systems and Broadcasting, pp. 1-4, 2014, doi: 10.1109/bmsb.2014.6873482.
[25] Y. Liu and Z. Qin, "A Chaotic Image Encryption Scheme Based on Henon-chebyshev Modulation Map and genetic Operation," Internationaljournal of Bifurcation andChaos, vol. 30, 2020. [ Links ]
[26] T. Y. Wu, X. Fan, K. H. Wang, J. S. Pan, and CM. Chen, "Security Analysis and Improvement on an Image Encryption Algorithm Using Chebyshev Generator," Journal of Internet Technology, vol. 20, 2019. [ Links ]
[27] I. Yasser, M. A. Mohamed, A. S. Samra, and F.Khalifa, "A Chaotic-Based Encryption/Decryption Framework for Secure Multimedia Communications," Entropy, vol. 22, 2020, doi: 10.3390/e22111253. [ Links ]
[28] Q. Yin and C. Wang, "A new chaotic image encryption scheme using breadth-first search and dynamic diffusion," lnt. J. Bifurcation and Chaos, vol. 28, pp. 1-17, 2018, doi: 10.1142/S021812741850047. [ Links ]
[29] C. E. Shannon, "A mathematical theory of communication," Bell System Technical Journal, vol. 27, pp. 379-423 and 623-656, 1948. [ Links ]
[30] X. Wang, S. Lin, and Y. Li, "A chaotic image encryption scheme based on cat map and MMT permutation," Modern Physics Letters B, vol. 33, 2019. [ Links ]

Asmaa Hilmi is a PhD student in the Laboratory of Information and Communication Technologies (LabTIC) in National school of applied sciences of Tangier (ENSAT), Abdelmalek Essaadi University. She received her engineer diploma in network and telecom in 2016 from National school of applied sciences of elJadida (ENSAJ). Her research interests are visual cryptography and security analysis.

Soufiane Mezroui is a professor at national school of Applied Sciences of Tangier since 2015. His research interests focus on Number Thoery, Cryptography and its applications.

Ahmed El Oualkadi received PhD. degree in electrical engineering from the University of Poitiers, France, in 2004. From 2000 to 2003, he was a research assistant at the Electronics & Electrostatics Research Unit at the University of Poitiers, France. In 2004, he was an assistant professor at University Institute of Technology, Angoulême, France. He joined the Microelectronics Laboratory at the University Catholic of Louvain, Belgium in 2005, where he worked and managed various European and regional projects in the areas of wireless communication and sensor networking. Currently, he is a full professor and the head of the department of information and communication systems at the National school of applied sciences of Tangier, Abdelmalek Essaadi University in Morocco. He was the coordinator of the Graduate engineering program in Telecommunication Systems and Networks from 2014 to 2021. He has supervised several PhD and Masters theses and has been the principal investigator and the project manager for several international and bilateral research projects. His research interests include analog IC, microwave and RFIC design for wireless communication, power electronics, embedded system and wireless communications applications.














